ICM40607信号处理与滤波：掌握核心技术，提升数据质量


参考资源链接：[ICM40607六轴传感器中文资料翻译：无人机应用与特性详解](https://wenku.csdn.net/doc/6412b73ebe7fbd1778d499ae?spm=1055.2635.3001.10343)
# 1. ICM40607传感器概述

传感器是现代技术应用中的核心元件，它能将物理量或化学量转换为可处理的电子信号。ICM40607传感器是惯性测量单元（IMU）的一种，它能同时测量加速度和角速度，广泛应用于需要动态感知的各种设备中。本章将概述ICM40607传感器的基本组成，其应用场景以及对现代测量技术的重要性。

## 1.1 ICM40607传感器的组成

ICM40607传感器由多个精密的MEMS（微机电系统）元件组成，包括加速度计、陀螺仪和可能的其他传感器，例如磁力计。通过将这些传感器的输出组合，可以为系统提供关于其运动状态的全面信息。

## 1.2 应用场景与重要性

这种传感器在汽车安全系统、手机、游戏控制器、VR头盔和工业机器人的运动跟踪中扮演着重要角色。它的精确度和响应速度是实现这些应用中精准动作和交互的关键。

## 1.3 ICM40607与现代测量技术

在现代测量技术中，ICM40607提供了一个高性价比的选择，适用于需要低成本但高性能应用的场合。其紧凑的设计和低功耗特性使其成为设计人员的首选。

在介绍完ICM40607传感器的基础知识后，接下来的章节将深入探讨其信号处理的基础和实践方法，为读者提供一个全面的技术理解和操作指南。

# 2. ICM40607信号处理基础

## 2.1 信号处理理论

### 2.1.1 信号的分类与特性

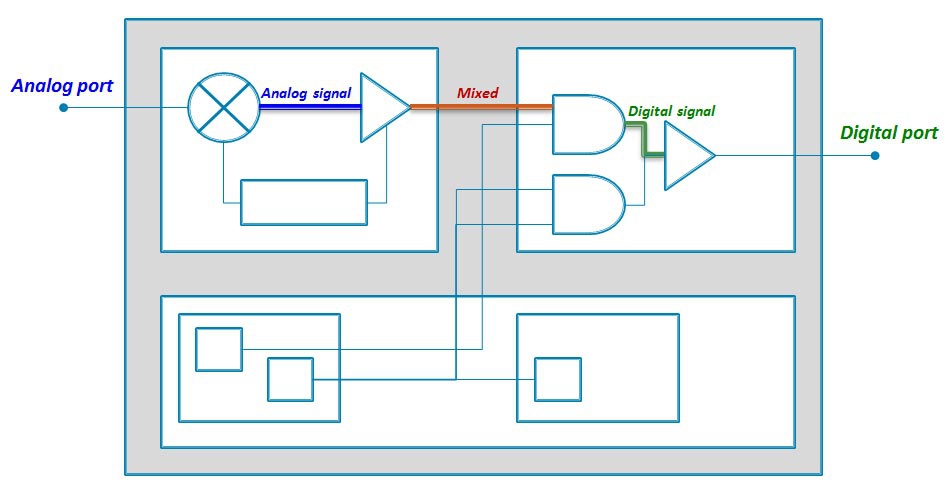
信号是信息的载体，是随时间变化的量，它承载着特定的信息内容，可以通过多种方式表示。在ICM40607传感器中，信号可以分为模拟信号和数字信号。

- **模拟信号**：模拟信号是连续变化的信号，可以是电压、电流、温度等物理量的连续变化。模拟信号的一个典型特性是它们可以在任意精度下表示连续的值，但是易受噪声干扰且在传输过程中可能损失部分信息。

- **数字信号**：与模拟信号相对，数字信号是离散的，它由一系列的0和1组成。数字信号具有良好的抗干扰性，并且在处理、存储和传输过程中可以保持原始信号的完整性。数字信号处理是现代通信和传感器技术的基石。

### 2.1.2 常用信号处理方法

在信号处理中，我们通常关注信号的增强、提取和压缩等几个方面，常用的信号处理方法包括：

- **滤波**：通过滤波可以去除信号中的噪声，或者提取特定频率的信号成分。滤波分为低通、高通、带通和带阻几种类型。

- **放大与衰减**：信号的增益调节，放大是为了提高信号的幅度以适应后续处理的要求，而衰减则是为了防止过载或者保护后续电路。

- **调制与解调**：调制是将信息信号加载到一个高频的载波上，通过调制过程可以实现信号的传输。解调是调制的逆过程，用于从调制信号中恢复信息。

## 2.2 滤波器设计原理

### 2.2.1 滤波器的基本概念和分类

滤波器是信号处理中用来对信号频率进行选择性过滤的设备或算法。其基本任务是允许某些频率的信号通过而阻止其他频率的信号，从而达到改变信号频谱的目的。

- **模拟滤波器**：使用电阻、电容和电感等电子元件设计，处理连续的模拟信号。

- **数字滤波器**：使用算法在数字处理器上实现，处理离散的数字信号。与模拟滤波器相比，数字滤波器更容易调整参数，且可以实现更复杂的滤波功能。

### 2.2.2 数字滤波器设计方法

设计数字滤波器时，我们通常需要考虑以下步骤：

1. 确定滤波器的技术指标，如通带频率、阻带频率、通带纹波和阻带衰减。
2. 根据技术指标选择合适的滤波器类型，比如FIR（有限脉冲响应）滤波器或IIR（无限脉冲响应）滤波器。
3. 设计滤波器系数，这可以通过窗函数法、频率采样法或最优化算法来实现。
4. 仿真验证滤波器的性能是否满足设计要求。
5. 如果需要，在实际硬件上实现滤波器，并进行测试和微调。

## 2.3 信号的采样与量化

### 2.3.1 采样定理和采样过程

根据奈奎斯特采样定理，为了无失真地恢复出原始的模拟信号，采样频率必须至少是信号最高频率成分的两倍。采样过程是将连续的模拟信号转换为离散时间信号的过程。

信号的采样可以通过模拟-数字转换器(ADC)来实现，将连续变化的模拟信号转换成离散的数字值。这个过程通常涉及到以下几个关键点：

- **采样速率**：决定了能够恢复的信号最高频率。
- **量化**：对采样后的信号进行数字编码，通常涉及将采样值映射到一个有限的值集中。
- **量化噪声**：由于量化过程中的信息损失产生的噪声。

### 2.3.2 量化误差和量化级别

量化误差是由于信号在数字化过程中由于无法精确表示无限精度的模拟值而产生的误差。量化级别决定了信号数字化的精度。

- **量化级别**：指定了ADC能够分辨的不同数字值的数量，这直接决定了信号的动态范围和分辨率。

量化级别越高，信号的细节保留得越多，但是这通常会导致更大的数据量和处理需求。在设计系统时，需要根据应用的需求权衡量化级别和系统的复杂性。

# 3. ICM40607信号处理实践

### 3.1 信号预处理技术

在信号处理领域，原始信号往往受到各种噪声的影响，导致其质量不高，难以直接用于分析和决策。因此，信号预处理技术显得尤为重要，它能够在数据进一步分析之前，显著提升信号的质量。

#### 3.1.1 去噪方法和原理

信号去噪是通过特定的技术方法减少或消除噪声，改善信号的信噪比。常见的去噪方法包括时域去噪、频域去噪以及自适应去噪等。

在时域去噪中，常用的方法有滑动平均滤波和中值滤波。滑动平均滤波是一种简单有效的去噪技术，通过取连续的几个采样点的平均值来估计信号值，从而降低噪声的影响。

import numpy as np

def moving_average_filter(data, window_size):
    filtered_data = np.convolve(data, np.ones(window_size)/window_size, mode='valid')
    return filtered_data

# 示例数据
noisy_signal = np.random.normal(0, 1, 100)  # 模拟带噪声的信号
window_size = 5  # 定义滤波窗口大小

# 应用滑动平均滤波
filtered_signal = moving_average_filter(noisy_signal, window_size)

# 输出去噪后的信号
print(filtered_signal)

频域去噪，则是基于傅里叶变换的原理，将信号从时域转换到频域，对信号频谱中的特定频率进行衰减或滤除，再通过逆傅里叶变换转换回时域。这种去噪技术适用于信号的特定噪声频率已知的情况。

自适应去噪方法，例如LMS（最小均方）算法，能够根据信号的特性动态调整滤波器的参数，以达到最佳的去噪效果。

#### 3.1.2 增益调整和信号平滑

除了去噪之外，信号的增益调整和信号平滑也是信号预处理中非常关键的步骤。增益调整通常是指将信号的幅度调整到一个适合进一步处理的范围内。适当的增益调整可以保证信号不丢失重要信息，同时避免超出处理系统的动态范围。

信号平滑的目的在于去除信号中的高频噪声，保留低频信息。通过平滑处理，可以减少噪声对信号分析结果的影响。常用的平滑方法包括移动平均法和高斯平滑等。

def gaussian_smoothing(signal, kernel_size):
    kernel = np.exp(-np.linspace(-3, 3, kernel_size) ** 2)
    kernel /= np.sum(kernel)
    smoothed_signal = np.convolve(signal, kernel, mode='same')
    return smoothed_signal

# 示例数据
signal = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])  # 示例信号
kernel_size = 7  # 定义高斯核大小

# 应用高斯平滑
smoothed_signal = gaussian_smoothing(signal, kernel_size)

# 输出平滑后的信号
print(smoothed_signal)

### 3.2 滤波器的实现与应用

在信号处理中，滤波器起着至关重要的作用。滤波器可以有效隔除信号中不需要的部分（如噪声），同时保留我们感兴趣的部分（如特定频率的信号）。本小节将探讨FIR和IIR滤波器的实现及其在实际应用中的优化。

#### 3.2.1 FIR和IIR滤波器的实现

FIR（有限脉冲响应）滤波器和IIR（无限脉冲响应）滤波器是两种主要的数字滤波器类型。FIR滤波器因其线性相位特性而受到青睐，在许多要求严格相位失真控制的应用中表现出色。相比之下，IIR滤波器通常可以使用更少的系数实现更陡峭的滚降特性，但可能存在稳定性问题。

FIR滤波器的设计通常使用窗函数法或最小二乘法等。在设计时，会确定滤波器的阶数和窗口类型，以满足特定的应用需求。下面是一个使用Python的SciPy库实现FIR滤波器的示例：

from scipy.signal import firwin, lfilter
import matplotlib.pyplot as plt

# 设计一个低通FIR