超越二分搜索:牛耕式算法创新研究的3个新视角
发布时间: 2025-01-10 14:01:44 阅读量: 6 订阅数: 8 


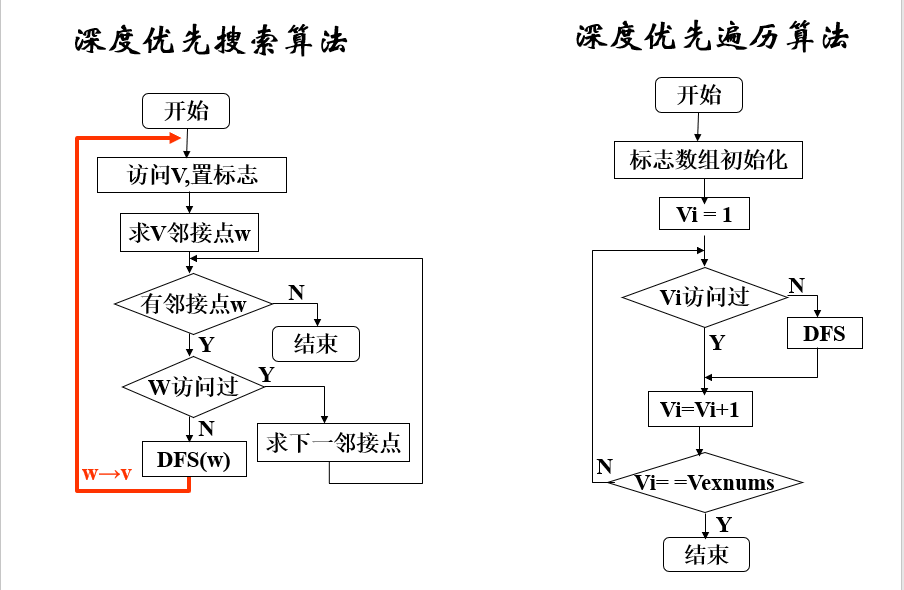
牛耕式分区-boustrophedon栅格图分区
# 摘要
本文介绍了一种新型的牛耕式算法,并通过与传统二分搜索算法对比,详细探讨了其基本原理、时间与空间复杂度以及适用性。在理论创新方面,文章分析了算法的数学模型、效率评估及稳健性研究。实践应用部分着重于牛耕式算法在实际问题求解中的建模、性能测试和案例研究。文章还探讨了算法在多线程、并行处理、分布式系统以及与机器学习技术融合方面的扩展研究,并对未来的理论与实践研究方向进行了展望。最后,文章讨论了牛耕式算法在教育领域的意义、推广策略及其对社会创新和发展的潜在影响。
# 关键字
牛耕式算法;二分搜索;时间复杂度;空间复杂度;理论创新;实践应用
参考资源链接:[二分搜索牛耕式全覆盖算法在静态障碍环境中的应用](https://wenku.csdn.net/doc/6412b739be7fbd1778d4989c?spm=1055.2635.3001.10343)
# 1. 牛耕式算法简介
## 1.1 算法的起源与发展
牛耕式算法是近年来针对特定数据结构优化的搜索算法,旨在解决传统二分搜索在某些特定应用中的局限性。它取名为“牛耕式”,是因为其核心思想如同农民犁田一般,细致地遍历数据集中的每一个区域,从而提高搜索精度。尽管它不是最快的搜索算法,但其在数据量较小且数据分布具有一定规律的场景下表现尤为突出。
## 1.2 算法的核心优势
该算法相较于二分搜索,在处理某些非标准数据结构时,能保持较高的稳定性和准确性。它通过逐步缩小搜索范围,并在必要时进行精细的局部搜索,避免了二分搜索在特定场景下效率低下的问题。在实际应用中,例如在数据预处理和特征提取阶段,牛耕式算法的这一特点能够显著提升算法整体的性能和稳定性。
## 1.3 应用领域和前景展望
牛耕式算法特别适用于需要对小规模数据集进行高效精确搜索的场景,比如在金融领域的异常检测、医疗影像分析中的病变区域定位等。随着技术的发展和数据处理需求的增加,牛耕式算法凭借其独特的优势,预计将有更广阔的应用前景和研究空间。
# 2. 牛耕式算法与传统二分搜索的比较
### 2.1 算法的基本原理对比
#### 2.1.1 牛耕式算法原理
牛耕式算法是一种从古代农业耕作方式中得到启发的搜索算法。其核心思想是将数据集分为若干等份,然后像耕牛犁田一样依次遍历这些份段。在每个份段中,再应用某种搜索机制来定位目标值。这种方法特别适用于部分数据结构,例如已排序且分割明显的数组。牛耕式算法在执行搜索时,初始将数组分为多个子数组,然后在各子数组内顺序遍历,直到找到目标值或者遍历完所有子数组。
```python
def ox_plowing_search(data, target):
# 将数据集分为若干份
sub_arrays = divide_data(data)
# 顺序遍历每个子数组
for sub_array in sub_arrays:
# 在子数组内顺序查找目标值
for item in sub_array:
if item == target:
return item
return None # 如果未找到目标值则返回None
```
上述代码表示了牛耕式搜索算法的基本逻辑。通过将数据集`data`分割成`sub_arrays`,然后依次遍历这些子数组来查找目标值`target`。需要注意的是,在实际应用中,分段的策略和子数组的遍历策略需要根据具体数据结构进行调整。
#### 2.1.2 二分搜索算法原理
二分搜索算法是一种高效的查找算法,其基本思想是在有序数组中通过不断将搜索区间减半来查找目标值。每次将区间中值与目标值进行比较,根据比较结果来决定是选择左半区间还是右半区间继续查找,直至找到目标值或区间为空。
```python
def binary_search(data, target):
left, right = 0, len(data) - 1
while left <= right:
mid = (left + right) // 2
if data[mid] == target:
return mid
elif data[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1 # 如果未找到目标值则返回-1
```
二分搜索算法相较于牛耕式算法,在最坏情况下具有对数时间复杂度的优势,但它仅适用于有序数据集。在有序数组中,通过折半的策略,二分搜索算法可以快速定位目标值的索引。
### 2.2 时间复杂度与空间复杂度分析
#### 2.2.1 牛耕式算法的时间复杂度
牛耕式算法的时间复杂度受到数据集分割策略的影响。在最坏的情况下,如果数据集被分为n个子数组,每个子数组被顺序遍历,那么时间复杂度为O(n)。在理想情况下,如果数据集可以被平均分割,并且目标值在第一个被遍历的子数组中,则时间复杂度为O(1)。
#### 2.2.2 牛耕式算法的空间复杂度
牛耕式算法的空间复杂度主要取决于数据集分割的数量。如果需要n份子数组来存储数据,那么空间复杂度将是O(n)。在不创建子数组而是遍历原数组的情况下,空间复杂度为O(1),因为它不需要额外的存储空间。
#### 2.2.3 与二分搜索的复杂度对比
二分搜索的时间复杂度在最坏和最好的情况下均为O(log n),因为它每次都能排除一半的数据,这在牛耕式算法中是无法实现的。二分搜索算法不需要额外的存储空间,因此其空间复杂度为O(1)。
### 2.3 算法适用性探讨
#### 2.3.1 特定应用场景分析
牛耕式算法适用于那些可以被高效分割的数据集,尤其是在数据集具有某种固有结构时。例如,在处理图像像素数据时,可以根据像素颜色分布将图像分块处理,然后在每个块中进行快速搜索。而在二分搜索中,如果数据集不是完全有序,那么二分搜索将不适用。
#### 2.3.2 算法的优缺点总结
牛耕式算法的主要优点是其对特定数据结构的适用性以及实现的简单性。但其缺点也很明显,即在最坏情况下可能需要顺序遍历大部分甚至所有数据,效率较低。二分搜索算法的优点在于其对数时间复杂度的高效率,但其适用范围受到数据集有序性的限制。在处理大体积、部分有序或未排序的数据集时,牛耕式算法往往比二分搜索更加灵活。
```markdown
表格1:牛耕式算法与二分搜索算法优缺点对比
| 算法 | 优点 | 缺点 |
| --- | --- | --- |
| 牛耕式 | 对特定数据结构适用性强;实现简单 | 在最坏情况下效率较低 |
| 二分搜索 | 时间复杂度低(O(log n));适用于有序数据集 | 适用范围受限;对数据有序性有要求 |
```
在上述表格中,我们清晰地对比了两种算法的优缺点。通过这种方式,读者可以更直观地理解每种算法在不同场景下的应用价值。
# 3. 牛耕式算法的理论创新
在深入探讨牛耕式算法的理论创新之前,首先需要明确算法理论基础的重要性。理论基础是算法开发和优化的根基,对于保证算法效率和稳健性至关重要。本章将从算法的理论拓展、效率分析以及稳健性研究三个方面,全面剖析牛耕式算法的创新点和改进策略。
## 3.1 算法理论基础的拓展
### 3.1.1 数学模型的构建
牛耕式算法的理论创新首先要从数学模型的构建开始。数学模型是算法的理论框架,它需要准确描述算法解决问题的过程和方法。对于牛耕式算法而言,其核心在于将一个复杂问题分解为一系列子问题,并且在每个子问题中应用特定的处理规则。
构建数学模型的关键步骤包括:
1. 定义问题空间:明确算法所要解决的问题的集合,以及每个子问题的范围和约束条件。
2. 描述子问题关系:通过数学关系式表达子问题之间的相互作用和依赖关系。
3. 规则化处理:为每个子问题制定具体的处理规则和操作步骤。
构建的数学模型不仅需要数学上的严谨性,更需要在实践中具有可行性。因此,模型的构建往往需要在理论分析和实验验证之间进行迭代优化。
### 3.1.2 理论模型的优化方法
在建立了初步的数学模型之后,下一步是对其进一步优化。优化的目标是提高算法的效率和适应性,减少资源
0
0





