软件测试中的统计技术：概率论带你优化测试案例设计到极致


# 摘要
本文探讨了概率论在软件测试中的应用及其重要性，从基础概率概念到复杂系统测试，论述了概率论如何指导测试案例的设计、优化以及缺陷定位。文章通过分析随机事件、概率分布、统计假设检验等基本原理，展示了概率论在提高测试覆盖率和效率、优化性能测试、安全漏洞评估以及自动化测试策略中的应用。案例分析部分具体阐述了概率论在功能测试、安全测试及自动化测试中的实际应用效果。最后，本文讨论了概率论在复杂系统测试和人工智能融合中的高级应用，并展望了概率论在未来测试领域面临的挑战和潜力。

# 关键字
概率论；软件测试；测试案例设计；缺陷定位；性能测试；自动化测试

参考资源链接：[概率论与数理统计（茆诗松）第二版课后习题参考答案](https://wenku.csdn.net/doc/6412b744be7fbd1778d49af6?spm=1055.2635.3001.10343)
# 1. 概率论在软件测试中的重要性

软件测试作为保证软件质量和可靠性的重要手段，在开发过程中扮演着核心角色。然而，随着软件系统的日益复杂化，传统的测试方法越来越难以应对新的挑战。在此背景下，概率论作为一种数学理论工具，在软件测试中的作用变得尤为重要。

概率论能够帮助测试工程师量化不确定性，通过概率模型对软件行为进行建模，从而更加科学地设计测试案例、分析测试结果，并预测软件可能出现的问题。此外，概率论的应用还能够指导测试资源的优化分配，提高测试效率和质量。

在本章中，我们将探究概率论在软件测试中的基本概念和重要性，以及如何将这些数学原理应用于实际的测试活动中，为软件测试的深度和广度提供理论支持和实践指导。接下来的章节将深入分析概率论在测试案例设计、测试案例优化实践以及案例分析中的具体应用。

# 2. 概率基础与测试案例设计

## 2.1 概率论的基本概念

### 2.1.1 随机事件与概率

在软件测试中，随机事件是测试过程中可能发生的任意现象，其结果是不确定的。比如，某个功能模块在测试中是否会发生故障就是一个随机事件。概率则是衡量随机事件发生可能性大小的数学工具，通常表示为一个介于0到1之间的数值。概率为1表示事件必定发生，概率为0表示事件不可能发生，而概率为0.5则表示事件发生的可能性与不发生的可能性相等。

在设计测试案例时，理解随机事件和概率是非常重要的。测试人员需要评估每个测试案例可能捕获的缺陷类型及其概率。例如，历史数据显示某个模块经常出现的错误类型，测试人员可以有针对性地设计测试案例来提高缺陷检测率。

### 2.1.2 条件概率与贝叶斯定理

条件概率指的是在某些条件或者事件已经发生的情况下，其他事件发生的概率。在软件测试中，可以用来分析在某个特定环境下软件失败的条件概率。

贝叶斯定理是一种描述条件概率之间关系的数学定理，它允许我们根据先验知识（已知概率）来计算后验概率（在一些条件下发生的概率）。在测试中，贝叶斯定理可以用来更新测试结果的概率解释。例如，在发现一个软件缺陷后，贝叶斯定理可以帮助我们更新未来在类似情况下发现缺陷的概率。

#### 代码块示例

# 一个简单的条件概率计算示例
# 假设有一个函数来模拟软件测试中的随机事件
def test_software():
    # 模拟一个随机事件
    return random.choice(['pass', 'fail'])

# 计算软件失败的条件概率
def calculate_conditional_probability(software_failure):
    # 假设我们有一个先验概率的估计
    prior_failure_rate = 0.1  # 基于历史数据得出的失败率

    # 当前测试结果为失败
    current_test_result = 'fail'

    # 当前的测试案例中软件失败的概率
    failure_rate = 0.2  # 假设失败率是0.2

    # 使用贝叶斯定理更新失败概率
    posterior_failure_rate = (failure_rate * software_failure) / prior_failure_rate
    return posterior_failure_rate

# 执行函数并获取结果
print(calculate_conditional_probability(test_software()))

## 2.2 概率分布与测试案例选择

### 2.2.1 常见的概率分布类型

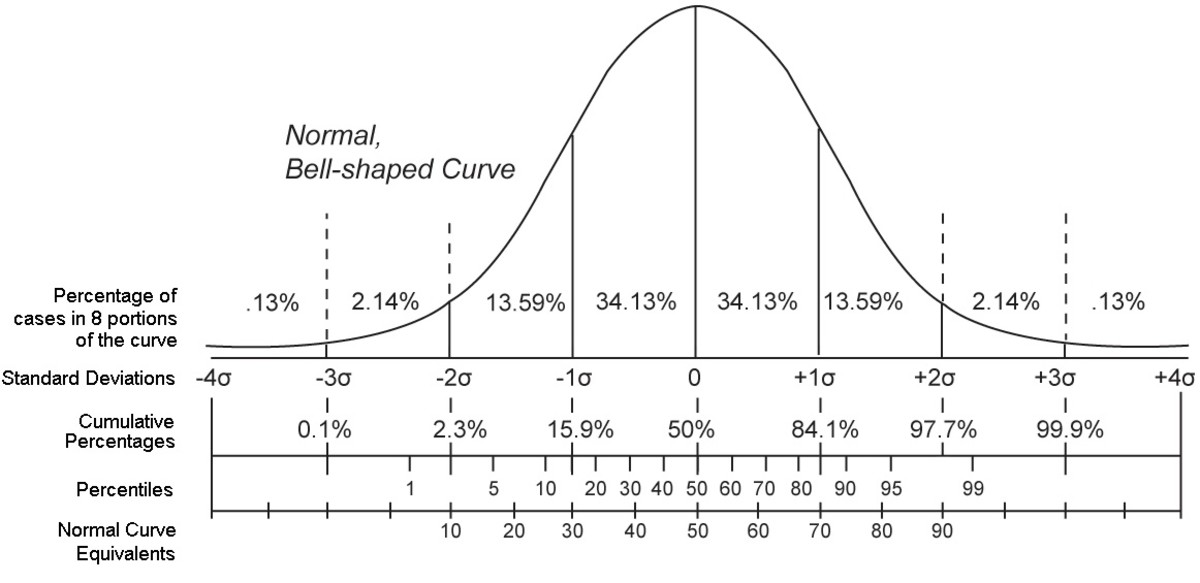
在概率论中，概率分布是描述随机变量取值及其概率的函数。在软件测试中，利用不同的概率分布类型可以帮助测试人员选择具有代表性和效率的测试案例。常见的概率分布类型包括均匀分布、正态分布和泊松分布等。

- **均匀分布**：在测试中，如果每个测试案例导致软件失败的概率相同，可以使用均匀分布来选择测试案例。
- **正态分布**：如果测试案例的效果符合“中间多，两端少”的规律，可以使用正态分布来选择测试案例。
- **泊松分布**：这种分布常用于描述一定时间或空间内随机事件发生的次数，非常适合于描述缺陷的发生。

### 2.2.2 应用概率分布优化案例选择

利用概率分布优化测试案例选择，可以提高测试的效率和覆盖率。例如，可以通过历史缺陷数据构建一个正态分布模型，然后根据这个模型选择测试案例，这样可以确保覆盖了高概率发生缺陷的区域。

#### 代码块示例

import numpy as np
import matplotlib.pyplot as plt

# 使用正态分布来选择测试案例
def select_test_cases(normal_distribution, num_cases):
    # 从分布中随机抽取测试案例
    test_cases = np.random.normal(normal_distribution['mean'], normal_distribution['std'], num_cases)
    return test_cases

# 定义正态分布参数
mean = 50  # 均值
std = 10   # 标准差

# 选择100个测试案例
selected_cases = select_test_cases({'mean': mean, 'std': std}, 100)

# 绘制直方图展示选取的测试案例
plt.hist(selected_cases, bins=10, density=True)
plt.show()

## 2.3 统计假设检验在测试中的应用

### 2.3.1 假设检验的基本原理

统计假设检验是统计学中的一个基本概念，它用于确定两个假设之间的差异是否具有统计学上的显著性。在软件测试中，可以用来验证测试结果是否显著不同，比如评估新版本的软件是否真的比旧版本更加稳定。

一个典型的假设检验包括提出假设、选择适当的统计模型、收集数据、进行统计测试、得出结论等步骤。在这个过程中，P值是一个非常重要的概念，它表示在零假设成立的情况下观察到当前或更极端结果的概率。

### 2.3.2 实际案例中的假设检验应用

在测试中应用假设检验，可以帮助测试人员评估软件的改进是否有效。比如，在性能测试中，可以使用假设检验来分析新旧版本软件在性能上的差异是否显著。如果P值小于设定的显著性水平（例如0.05），则认为差异是统计上显著的，新版本软件性能的改进是可信的。

#### 表格示例

| 测试类型 | 软件版本 | 平均响应时间（秒） | 标准差 |
|----------|----------|-------------------|--------|
| 性能测试 | 版本A | 2.5 | 0.2 |
| 性能测试 | 版本B | 2.2 | 0.3 |

通过上表，我们可以设计一个假设检验来评估两个版本之间的响应时间是否存在显著差异。如果计算的P值小于0.05，我们将拒绝零假设，接受响应时间有显著差异的备择假设。

#### 代码块示例

from scipy.stats import ttest_ind

# 假设我们有两组性能测试数据
version_a = np.array([2.4, 2.6, 2.7, 2.5, 2.3])
version_b = np.array([2.1, 2.2, 2.3, 2.0, 2.4])