MATLAB复数在控制系统中的应用：揭秘复数在反馈回路中的作用，理解控制系统的本质

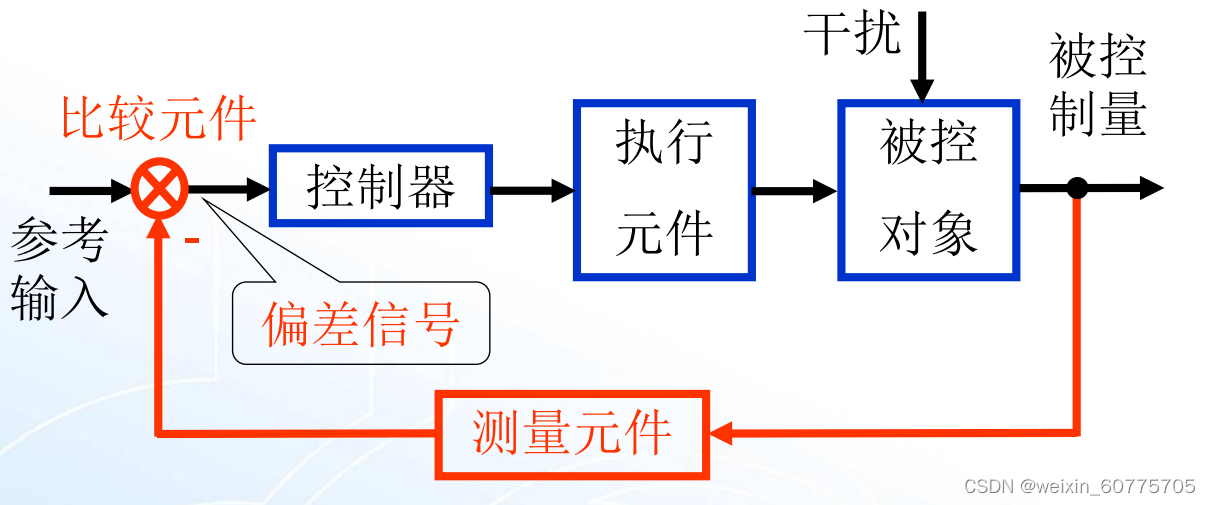
# 1. MATLAB复数简介**

MATLAB复数是表示具有实部和虚部的复数的特殊数据类型。它使用`complex`函数创建，语法为`complex(real_part, imaginary_part)`。例如，`complex(3, 4)`创建一个实部为3、虚部为4的复数。

复数在MATLAB中支持各种运算，包括加法、减法、乘法和除法。这些运算遵循复数运算的标准规则，其中`i`表示虚数单位。例如，`3 + 4i + 5 - 2i`计算为`8 + 2i`。

# 2. 复数在控制系统中的理论基础

### 2.1 复数的数学表示和运算

#### 2.1.1 复数的定义和表示

复数是一个包含实部和虚部的数字，通常表示为 `a + bi`，其中 `a` 是实部，`b` 是虚部，`i` 是虚数单位，满足 `i² = -1`。

复数可以用多种方式表示，包括笛卡尔形式（`a + bi`）、极坐标形式（`r∠θ`）和指数形式（`re^(iθ)`）。

#### 2.1.2 复数的加减乘除运算

复数的加减运算与实数类似，即实部与实部相加，虚部与虚部相加。乘除运算则需要用到虚数单位 `i` 的性质：

* `(a + bi) + (c + di) = (a + c) + (b + d)i`
* `(a + bi) - (c + di) = (a - c) + (b - d)i`
* `(a + bi) * (c + di) = (ac - bd) + (ad + bc)i`
* `(a + bi) / (c + di) = (ac + bd) / (c² + d²) + (bc - ad)i / (c² + d²)`

### 2.2 复数在控制系统中的意义

#### 2.2.1 复数表示系统传递函数

在控制系统中，传递函数通常用复数表示。传递函数是系统输出与输入之间的关系，可以用以下形式表示：

G(s) = N(s) / D(s)

其中 `s` 是复频率变量，`N(s)` 和 `D(s)` 是多项式。

#### 2.2.2 复数表示系统频率响应

复数也可以用来表示系统的频率响应。频率响应是系统输出对正弦输入的响应，可以用以下形式表示：

H(jω) = G(jω) = |H(jω)|∠∠H(jω)

其中 `jω` 是复频率，`|H(jω)|` 是幅度响应，`∠H(jω)` 是相位响应。

复数在控制系统中具有重要的意义，它可以表示系统的传递函数和频率响应，为系统分析和设计提供了有力的工具。

# 3. 复数在控制系统中的实践应用

复数在控制系统中具有广泛的实践应用，特别是在频率响应分析和控制系统设计中。

### 3.1 复数在频率响应分析中的应用

频率响应分析是控制系统分析和设计的重要工具。复数在频率响应分析中扮演着至关重要的角色，因为它可以表示系统的传递函数和频率响应。

#### 3.1.1 奈奎斯特图

奈奎斯特图是一种图形化工具，用于分析系统的稳定性和性能。它将系统的开环传递函数绘制在复数平面上，并通过评估图中的特定特征来确定系统的稳定性。

% 定义开环传递函数
num = [1];
den = [1, 2, 1];
G = tf(num, den);

% 绘制奈奎斯特图
figure;
nyquist(G);
title('奈奎斯特图');

**代码逻辑分析：**

* `tf` 函数用于创建传递函数对象 `G`，其中 `num` 和 `den` 分别表示传递函数的分子和分母。
* `nyquist` 函数绘制传递函数 `G` 的奈奎斯特图。

#### 3.1.2 波德图

波德图是另一种图形化工具，用于分析系统的频率响应。它将系统的开环传递函数绘制在两个图上：幅度-频率图和相位-频率图。

``