特征值问题解析:QR方法与原始特征值问题的关系
发布时间: 2024-03-31 01:02:56 阅读量: 53 订阅数: 61 

# 1. 特征值问题简介
- 1.1 特征值问题的定义与背景
- 1.2 特征值问题在科学计算中的重要性
# 2. QR方法概述
- 2.1 QR分解的基本原理与步骤
- 2.2 QR方法在特征值计算中的应用
# 3. 特征值问题的数学原理
在本章中,我们将深入探讨特征值问题的数学原理,包括其数学表达式和特征向量与特征值的关系。让我们一起来了解这些重要概念。
### 3.1 特征值问题的数学表达式
特征值问题通常可以表示为以下形式的线性代数方程:
对于一个n阶方阵A,存在一个标量λ和一个非零n维向量v,使得以下方程成立:
\[ Av = \lambda v \]
其中,λ是该矩阵A的特征值,v是对应于特征值λ的特征向量。
### 3.2 特征向量与特征值的关系
特征向量是在矩阵A作用下只发生伸缩变化的非零向量,特征值则是这种伸缩的比例系数。特征向量与特征值之间的关系可以用特征值问题的数学表达式来表示。
在实际计算中,我们通常通过求解特征值问题来找到矩阵的特征值和特征向量,这也是QR方法等算法的基础。
# 4. QR方法与原始特征值问题的联系
在这一章节中,我们将探讨QR方法与原始特征值问题之间的联系,以及QR方法如何用于解决原始特征值问题的具体方式。同时,我们还会对QR方法与传统特征值求解方法进行比较,以揭示QR方法的优势和局限性。让我们深入探讨如下内容:
### 4.1 QR方法如何用于解决原始特征值问题
特征值问题通常可以表示为矩阵 $A$ 的特征方程 $Ax = \lambda x$,其中 $A$ 是一个方阵,$x$ 是非零向量,$\lambda$ 是特征值。QR方法是一种数值求解特征值问题的方法,其基本思想是通过单位正交矩阵的递归因子分解,将矩阵 $A$ 转化为上三角矩阵 $R$,从而逐步求得矩阵 $A$ 的特征值。
具体步骤如下:
- 对给定的矩阵 $
 百万级
高质量VIP文章无限畅学
百万级
高质量VIP文章无限畅学
 千万级
优质资源任意下载
千万级
优质资源任意下载
 C知道
免费提问 ( 生成式Al产品 )
C知道
免费提问 ( 生成式Al产品 )
0
0
SW_孙维
开发技术专家
知名科技公司工程师,开发技术领域拥有丰富的工作经验和专业知识。曾负责设计和开发多个复杂的软件系统,涉及到大规模数据处理、分布式系统和高性能计算等方面。
专栏简介
本专栏将深入探讨Fortran编写QR方法求解特征值的各个方面。从简介QR分解在特征值求解中的基本原理开始,逐步介绍Fortran基础中如何进行QR分解,以及如何使用Householder变换实现QR方法。通过特征值问题解析,探讨QR方法与原始特征值问题的关系,并介绍如何优化QR方法以加速计算过程。进一步介绍Eigen库在Fortran中的应用,以及如何评估QR方法的数值稳定性。讨论利用Hessenberg矩阵优化QR方法,实例演练以及与LU分解的比较。同时也涉及将QR方法应用于并行计算,Shifted QR方法,迭代法与QR方法的关系,雅可比方法与QR方法的对比,广义特征值问题的拓展等内容。最后,探讨QR方法在图像处理中的应用,奇异值分解与QR分解的联系,以及QR算法在特征值求解中的新进展,旨在帮助读者深入了解QR方法在特征值求解中的实际应用与发展。
专栏目录
最低0.47元/天 解锁专栏
买1年送3月
 百万级
高质量VIP文章无限畅学
百万级
高质量VIP文章无限畅学
 千万级
优质资源任意下载
千万级
优质资源任意下载
 C知道
免费提问 ( 生成式Al产品 )
C知道
免费提问 ( 生成式Al产品 )
最新推荐
【系统兼容性深度揭秘】:Win10 x64上的TensorFlow与CUDA完美匹配指南
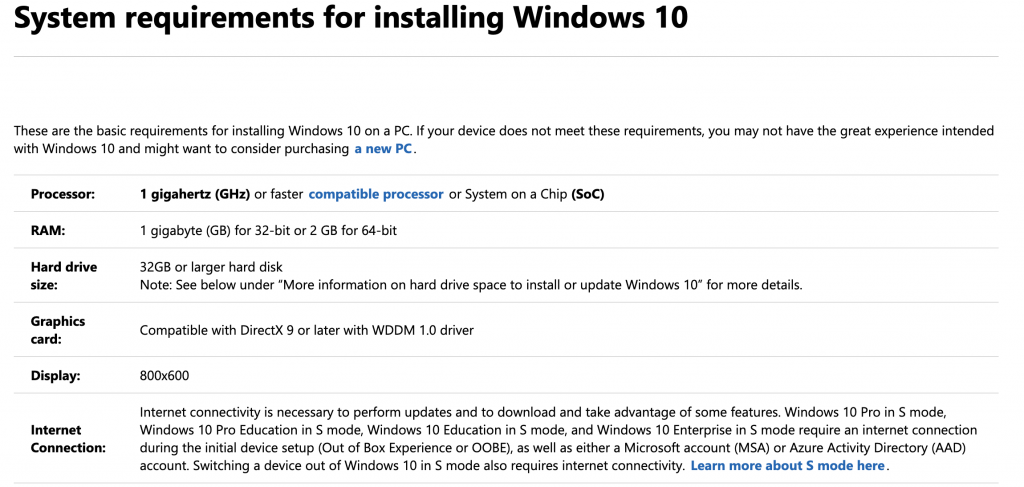
# 摘要
本文详细探讨了在深度学习框架中系统兼容性的重要性,并深入介绍了CUDA的安装、配置以及TensorFlow环境的搭建过程。文章分析了不同版本CUDA与GPU硬件及NVIDIA驱动程序的兼容性需求,并提供了详细的安装步骤和故障排除方法。针对TensorFlow的安装与环境搭建,文章阐述了版本选择、依赖
先农熵数学模型:计算方法深度解析

# 摘要
先农熵模型作为一门新兴的数学分支,在理论和实际应用中显示出其独特的重要性。本文首先介绍了先农熵模型的概述和理论基础,阐述了熵的起源、定义及其在信息论中的应用,并详细解释了先农熵的定义和数学角色。接着,文章深入探讨了先农熵模型的计算方法,包括统计学和数值算法,并分析了软件实现的考量。文中还通过多个应用场景和案例,展示了先农熵模型在金融分析、生物信息学和跨学科研究中的实际应用。最后,本文提出了
【24小时精通电磁场矩量法】:从零基础到专业应用的完整指南

# 摘要
本文系统地介绍了电磁场理论与矩量法的基本概念和应用。首先概述了电磁场与矩量法的基本理论,包括麦克斯韦方程组和电磁波的基础知识,随后深入探讨了矩量法的理论基础,特别是基函数与权函数选择、阻抗矩阵和导纳矩阵的构建。接着,文章详述了矩量法的计算步骤,涵盖了实施流程、编程实现以及结果分析与验证。此外,本文还探讨了矩量法在天线分析、微波工程以及雷达散射截面计算等不同场景的应用,并介绍了高频近似技术、加速技术和
RS485通信原理与实践:揭秘偏置电阻最佳值的计算方法
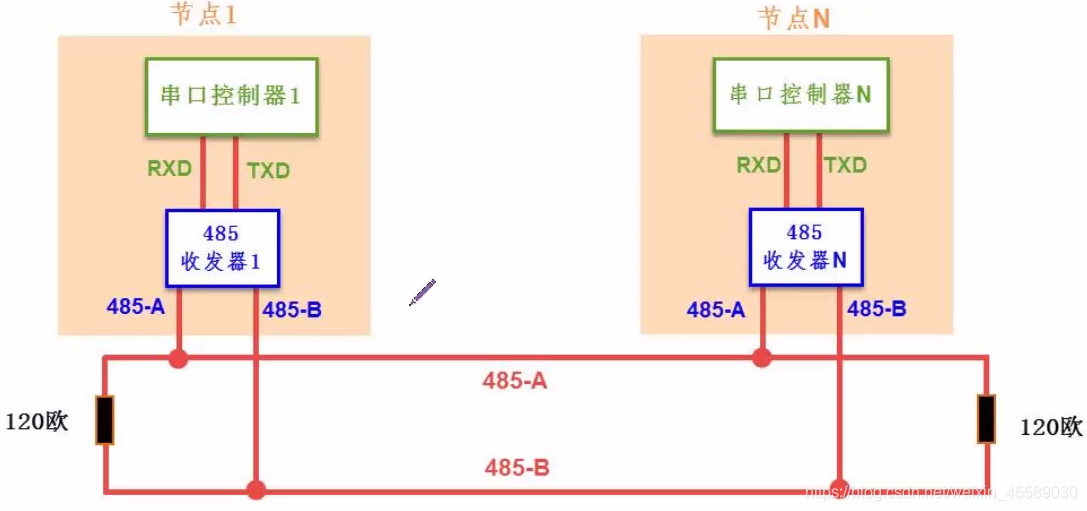
# 摘要
RS485通信作为一种广泛应用的串行通信技术,因其较高的抗干扰能力和远距离传输特性,在工业控制系统和智能设备领域具有重要地位。
【SOEM多线程编程秘籍】:线程同步与资源竞争的管理艺术

# 摘要
本文针对SOEM多线程编程提供了一个系统性的学习框架,涵盖多线程编程基础、同步机制、资源竞争处理、实践案例分析以及进阶技巧,并展望了未来发展趋势。首先,介绍了多线程编程的基本概念和线程同步机制,包括同步的必要性、锁的机制、同步工具的使用等。接着,深入探讨了资源竞争的识别、预防策略和调试技巧。随后
SRIO Gen2在嵌入式系统中的实现:设计要点与十大挑战分析

# 摘要
本文对SRIO Gen2技术在嵌入式系统中的应用进行了全面概述,探讨了设计要点、面临的挑战、实践应用以及未来发展趋势。首先,文章介绍了SRIO Gen2的基本概念及其在嵌入式系统中的系统架构和硬件设计考虑。随后,文章深入分析了SRIO Gen2在嵌入式系统中遇到的十大挑战,包括兼容性、性能瓶颈和实时性能要求。在实践应用方面,本文讨论了硬件设计、软件集成优化以及跨平台部署与维护的策略。最后,文章展望了SRI
【客户满意度提升神器】:EFQM模型在IT服务质量改进中的效果

# 摘要
本论文旨在深入分析EFQM模型在提升IT服务质量方面的作用和重要性。通过对EFQM模型基本原理、框架以及评估准则的阐述,本文揭示了其核心理念及实践策略,并探讨了如何有效实施该模型以改进服务流程和建立质量管理体系。案例研究部分强调了EFQM模型在实际IT服务中的成功应用,以及它如何促进服务创新和持续改进。最后,本论文讨论了应用EFQM模型时可能遇到的挑战,以及未来的发展趋势,包括
QZXing进阶技巧:如何优化二维码扫描速度与准确性?

# 摘要
随着移动设备和电子商务的迅速发展,QZXing作为一种广泛应用的二维码扫描技术,其性能直接影响用户体验。本文首先介绍了QZXing的基础知识及其应用场景,然后深入探讨了QZXing的理论架构,包括二维码编码机制、扫描流程解析,以及影响扫描速度与准确性的关键因素。为了优化扫描速度,文章提出了一系列实践策略,如调整解码算法、图像预处理技术,以及线程和并发优化。此外,本文还探讨了提升扫描准
【架构设计的挑战与机遇】:保险基础数据模型架构设计的思考

# 摘要
保险业务的高效运行离不开科学合理的架构设计,而基础数据模型作为架构的核心,对保险业务的数据化和管理至关重要。本文首先阐述了架构设计在保险业务中的重要性,随后介绍了保险基础数据模型的理论基础,包括定义、分类及其在保险领域的应用。在数据模型设计实践中,本文详细讨论了设计步骤、面向对象技术及数据库选择与部署
【AVR编程效率提升宝典】:遵循avrdude 6.3手册,实现开发流程优化
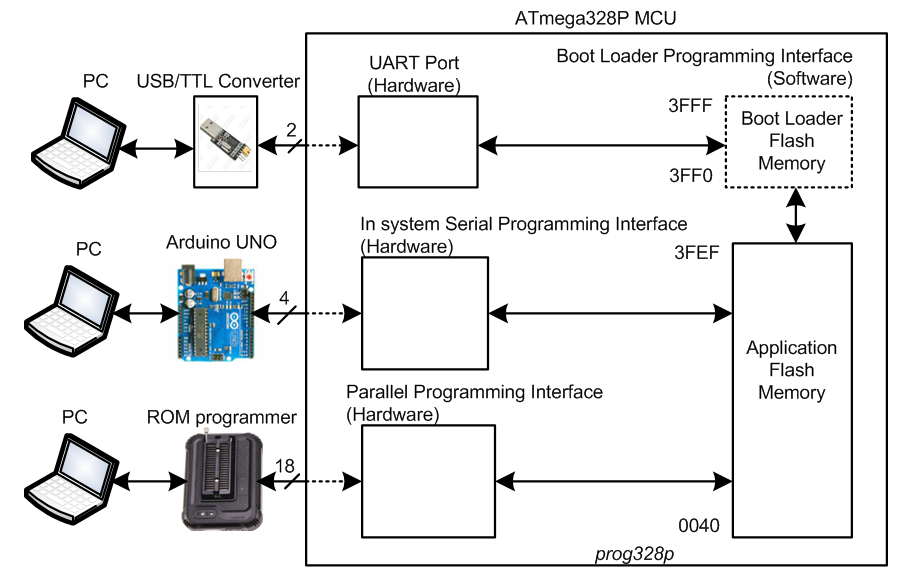
# 摘要
本文深入探讨了AVR编程和开发流程,重点分析了avrdude工具的使用与手册解读,从而为开发者提供了一个全面的指南。文章首先概述了avrdude工具的功能和架构,并进一步详细介绍了其安装、配置和在AVR开发中的应用。在开发流程优化方面,本文探讨了如何使用avrdude简化编译、烧录、验证和调
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



专栏目录
最低0.47元/天 解锁专栏
买1年送3月
 百万级
高质量VIP文章无限畅学
百万级
高质量VIP文章无限畅学
 千万级
优质资源任意下载
千万级
优质资源任意下载
 C知道
免费提问 ( 生成式Al产品 )
C知道
免费提问 ( 生成式Al产品 )
