MATLAB矩阵运算与机器学习：机器学习算法中的矩阵运算，揭秘算法背后的数学原理

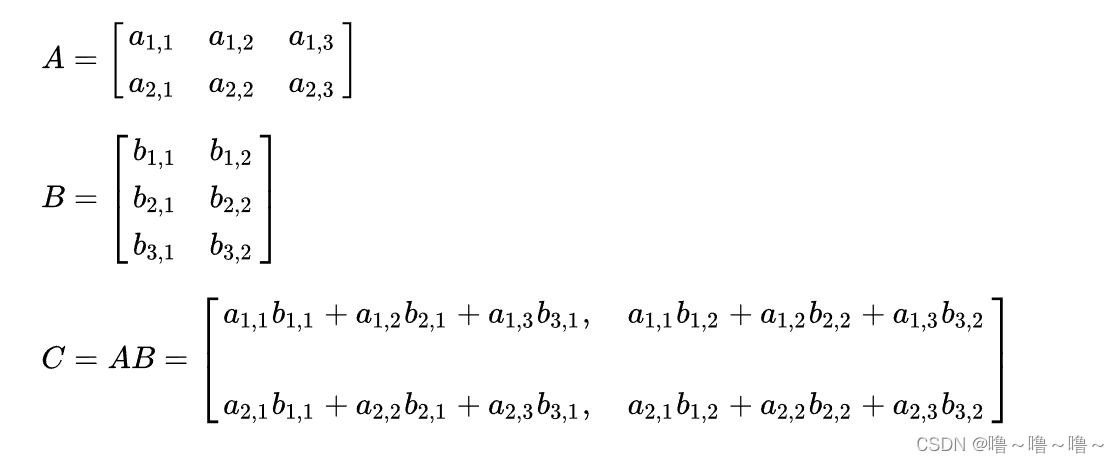
# 1. MATLAB矩阵运算基础

MATLAB是一种强大的编程语言，特别适合于矩阵运算。矩阵是一种数据结构，可以存储和操作大量数据。在MATLAB中，矩阵运算非常高效，并且提供了广泛的函数来执行各种操作。

本节将介绍MATLAB矩阵运算的基础知识，包括矩阵创建、访问元素、矩阵运算和矩阵函数。通过这些基础知识，您可以开始使用MATLAB进行更高级的矩阵运算，例如机器学习和数据分析。

# 2.1 矩阵分解与特征提取

### 2.1.1 奇异值分解（SVD）

奇异值分解（SVD）是一种将矩阵分解为三个矩阵的数学技术：

- **U：**左奇异向量矩阵，其列向量是 A 的左奇异向量。
- **Σ：**奇异值矩阵，是一个对角矩阵，其对角线元素是 A 的奇异值。
- **V：**右奇异向量矩阵，其列向量是 A 的右奇异向量。

**SVD 的数学表示：**

[U, S, V] = svd(A);

**代码逻辑分析：**

* `svd()` 函数接收一个矩阵 `A`，并将其分解为左奇异向量矩阵 `U`、奇异值矩阵 `S` 和右奇异向量矩阵 `V`。
* `U` 的列向量是 `A` 的左奇异向量，其长度为 `A` 的行数。
* `S` 是一个对角矩阵，其对角线元素是 `A` 的奇异值，奇异值是 `A` 的非负特征值。
* `V` 的列向量是 `A` 的右奇异向量，其长度为 `A` 的列数。

**参数说明：**

* `A：`要分解的矩阵。

### 2.1.2 主成分分析（PCA）

主成分分析（PCA）是一种降维技术，它通过找到数据中方差最大的方向来将高维数据投影到低维空间。

**PCA 的数学表示：**

[coeff, score, latent] = pca(X);

**代码逻辑分析：**

* `pca()` 函数接收一个数据矩阵 `X`，并返回：
* `coeff：`主成分载荷矩阵，其列向量是主成分。
* `score：`投影数据矩阵，其行向量是数据点在主成分上的投影。
* `latent：`方差矩阵，其对角线元素是主成分的方差。
* 主成分是数据中方差最大的方向，它们可以用来表示数据中的主要特征。
* 投影数据是数据点在主成分上的投影，它可以用来降维。

**参数说明：**

* `X：`要进行 PCA 的数据矩阵。

# 3. 机器学习算法中的矩阵运算实践

### 3.1 支持向量机（SVM）中的矩阵运算

#### 3.1.1 SVM的数学原理

支持向量机（SVM）是一种监督学习算法，用于分类和回归任务。其基本原理是将数据点映射到一个高维特征空间，并在该空间中寻找一个超平面，将不同类别的点分隔开来。

SVM的数学模型可以表示为：

max w^T x + b
s.t. y_i (w^T x_i + b) >= 1, i = 1, ..., n

其中：

* w 是超平面的权重向量
* x 是数据点
* b 是超平面的偏置
* y_i 是数据点的标签（+1 或 -1）

#### 3.1.2 SVM中的核函数

为了将数据点映射到高维特征空间，SVM使用核函数。核函数是一种将低维数据点映射到高维特征空间的函数，而无需显式地计算映射后的数据点。

常用的核函数包括：

* 线性核：K(x, y) = x^T y
* 多项式核：K(x, y) = (x^T y + c)^d
* RBF核：K(x, y) = exp(-γ ||x - y||^2)

### 3.2 决