掌握MATLAB优化算法：解决复杂优化问题，提升算法性能

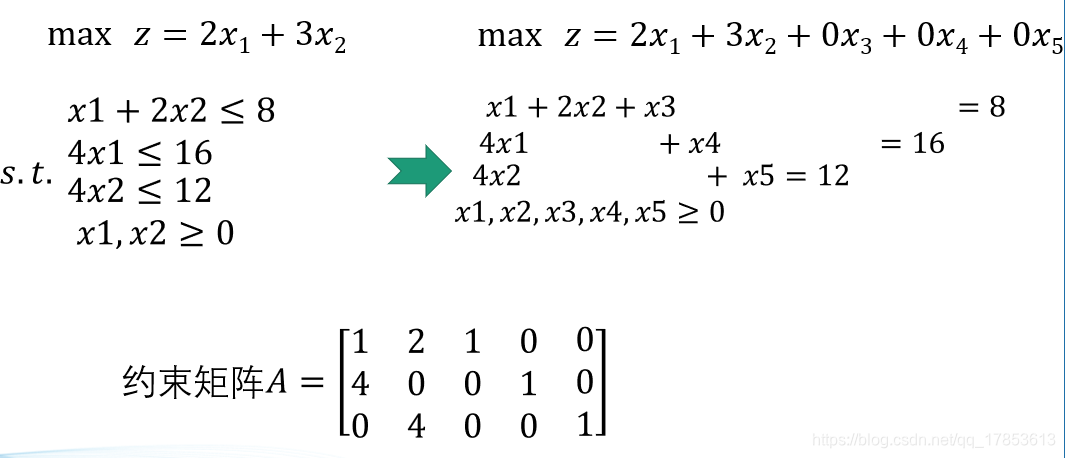
# 1. MATLAB优化算法概述**

优化算法是用于解决优化问题的数学工具，优化问题是指在给定约束条件下，寻找使目标函数达到最优值（最大值或最小值）的解。MATLAB提供了一系列强大的优化算法，可以高效地解决各种优化问题。

MATLAB优化算法的应用范围广泛，包括：

* **连续优化：**求解连续变量的目标函数，例如函数拟合、参数估计。
* **离散优化：**求解离散变量的目标函数，例如组合优化、排列优化。
* **约束优化：**求解满足约束条件的目标函数，例如线性规划、非线性规划。
* **多目标优化：**求解具有多个目标函数的目标函数，例如加权和法、NSGA-II算法。

# 2. MATLAB优化算法理论基础

### 2.1 优化问题类型和目标函数

优化问题是指在给定的约束条件下，寻找使目标函数达到最优（最小或最大）值的问题。优化问题可分为以下两类：

- **连续优化问题：**目标函数和约束条件都是连续的，变量可以取任意实数值。
- **离散优化问题：**目标函数或约束条件中至少有一个是离散的，变量只能取有限个离散值。

目标函数是优化问题中需要优化的函数，它表示要最小化或最大化的目标值。目标函数可以是线性、非线性、凸或非凸。

### 2.2 优化算法分类和原理

优化算法是用于求解优化问题的数学方法。优化算法可分为以下几类：

#### 2.2.1 梯度下降法

梯度下降法是一种迭代算法，它通过沿目标函数梯度方向移动来寻找最优值。梯度是目标函数在每个点处的导数向量，它表示目标函数在该点变化最快的方向。

梯度下降法的更新公式为：

x_{k+1} = x_k - α∇f(x_k)

其中：

- x_k 是第 k 次迭代的当前点
- x_{k+1} 是第 k+1 次迭代的更新点
- α 是学习率，控制步长大小
- ∇f(x_k) 是目标函数 f(x) 在点 x_k 的梯度

#### 2.2.2 牛顿法

牛顿法是一种二阶优化算法，它利用目标函数的二阶导数（海森矩阵）来加速收敛。牛顿法的更新公式为：

x_{k+1} = x_k - H(x_k)^{-1}∇f(x_k)

其中：

- H(x_k) 是目标函数 f(x) 在点 x_k 的海森矩阵

#### 2.2.3 遗传算法

遗传算法是一种基于自然选择和遗传学的启发式算法。它将候选解表示为染色体，并通过选择、交叉和变异等操作来生成新的解。遗传算法适用于离散优化问题和复杂非线性优化问题。

### 2.3 算法性能评价指标

优化算法的性能可以通过以下指标进行评价：

- **收敛速度：**算法达到给定精度所需迭代次数
- **收敛精度：**算法求得的最优值与真实最优值之间的误差
- **鲁棒性：**算法对初始值和参数设置的敏感性
- **计算复杂度：**算法所需的计算时间和空间资源

# 3. MATLAB优化算法实践应用

### 3.1 连续优化问题求解

连续优化问题是指求解一个连续函数的极值，即最大值或最小值。MATLAB提供了多种求解连续优化问题的函数，包括：

- `fminbnd`：一维有界优化
- `fminsearch`：多维无约束优化
- `fminunc`：多维有约束优化

#### 3.1.1 单变量优化

单变量优化问题是指求解一个一维函数的极值。MATLAB中可以使用`fminbnd`函数求解单变量优化问题。`fminbnd`函数的语法如下：

[x, fval] = fminbnd(fun, lower, upper)

其中：

- `fun`：一维函数的函数句柄
- `lower`：搜索下界
- `upper`：搜索上界

例如，求解函数 `f(x) = x^2 - 2x` 在区间 `[0, 1]` 上的最小值：

fun = @(x) x^2 - 2*x;
[x, fval] = fminbnd(fun, 0, 1);

#### 3.1.2 多变量优化

多变量优化问题是指求解一个多维函数的极值。MATLAB中可以使用`fminsearch`和`fminunc`函数求解多变量优化问题。

- `fminsearch`：多维无约束优化
- `fminunc`：多维有约束优化

`fminsearch`函数的语法如下：

[x, fval] = fminsearch(fun, x0)

其中：

- `fun`：多维函数的函数句柄
- `x0`：初始猜测值

例如，求解函数 `f(x, y) = x^2 + y^2` 在初始猜测值 `x0 = [1, 1]` 处的最小值：

fun = @(x) x(1)^2 + x(2)^2;
x0 = [1, 1];
[x, fval] = fminsearch(fun, x0);

`fminunc`函数的语法如下：

[x, fval] = fminunc(fun, x0, options)

其中：

- `fun`：多维函数的函数句柄
- `x0`：初始猜测值
- `options`：优化选项

例如，求解函数 `f(x, y) = x^2 + y^2` 在初始猜测值 `x0 = [1, 1]` 处的最小值，并设置最大迭代次数为 100：

fun = @(x) x(1)^2 + x(2)^2;
x0 = [1, 1];
options