SPSS与MATLAB效率对决：绘制置信区间的全面对比与优化策略

目录
1. 统计学中的置信区间概念解析

1.1 置信区间的定义与意义
1.2 置信区间的计算方法

2. SPSS在置信区间绘制中的应用

2.1 SPSS的基本操作和置信区间计算

2.1.1 SPSS界面和功能概述
2.1.2 数据导入与基本统计操作

2.2 SPSS绘制置信区间的详细步骤

2.2.1 选择合适的置信区间计算方法
2.2.2 输出结果的解读与注意事项

2.3 SPSS在置信区间应用中的优势与局限

2.3.1 SPSS用户界面友好性分析
2.3.2 SPSS在处理特定数据集的效率

解锁专栏，查看完整目录
参考资源链接：SPSS、Matlab与Sigmaplot绘制线性回归置信区间详解
1. 统计学中的置信区间概念解析
在统计学领域，置信区间是一个非常基础且重要的概念，是研究数据并进行推断统计的重要工具。简单来说，置信区间是对某个总体参数（如均值、比例等）的可能值的区间估计。它不仅可以帮助我们了解数据的分布情况，还能使我们在一定程度上把握对总体参数的估计准确性。
1.1 置信区间的定义与意义
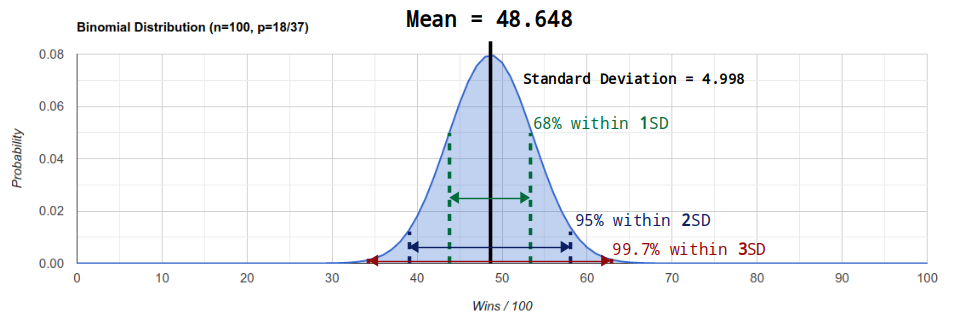
置信区间是由一个样本统计量（如样本均值）和一个围绕它的区间组成的，这个区间具有一定的置信水平，通常称为置信度。例如，当我们说95%的置信区间时，意味着如果我们从总体中反复抽取样本并计算置信区间，有95%的置信区间会包含总体参数的真实值。这个定义强调了置信区间的一个关键特性——它是一个概率表述，而非确定性结论。
1.2 置信区间的计算方法
计算置信区间通常涉及样本数据和一个概率分布（例如正态分布）。具体的计算方法取决于样本数据的分布特性和所需置信度。例如，对于大样本，我们通常使用样本标准误差和t分布来计算均值的置信区间；而对于二项分布比例的置信区间，我们会用到正态近似法或者精确的二项概率公式。
本章我们初步了解了置信区间的概念、意义和基本的计算方法。随后的章节将分别探讨SPSS和MATLAB在绘制置信区间中的应用和操作流程，以及这两种软件在实际使用中的优势和局限性。
2. SPSS在置信区间绘制中的应用
2.1 SPSS的基本操作和置信区间计算
2.1.1 SPSS界面和功能概述
SPSS（Statistical Package for the Social Sciences）是一款广泛应用于社会科学统计分析的软件。它提供了一系列的数据管理和分析工具，可以用于执行多种统计测试，包括置信区间的计算。用户界面直观易用，通过菜单栏、工具栏和数据视图窗口，用户可以轻松进行数据的输入、编辑以及后续的统计分析。
在功能上，SPSS涵盖了描述性统计、假设检验、相关与回归分析、多变量分析等多种统计方法。对于置信区间的计算，SPSS提供了一系列专门的命令和选项，用户无需编程即可快速得到结果。
2.1.2 数据导入与基本统计操作
数据导入是使用SPSS进行统计分析的第一步。SPSS支持多种数据格式的导入，如Excel、文本文件以及各种数据库格式。导入数据后，可以使用数据视图窗口对数据进行查看和编辑，如调整变量类型、设置缺失值等。
在数据准备完毕后，可以进行基本的描述性统计分析，以便了解数据的基本特征。SPSS中描述性分析选项位于“分析”菜单下的“描述统计”子菜单中。用户可以对单个变量或多变量同时进行描述性统计，获得均值、标准差、最小值、最大值等统计量。
2.2 SPSS绘制置信区间的详细步骤
2.2.1 选择合适的置信区间计算方法
在SPSS中，计算置信区间有多种方法，包括基于均值、比例、中位数等的置信区间计算。选择哪种方法取决于研究目标和数据的性质。例如，对于连续型数据，通常使用均值的置信区间；对于二项分布数据，则使用比例的置信区间。
选择计算方法的步骤如下：

在SPSS菜单栏中选择“分析”菜单，然后选择“描述统计” -> “探索”。
在弹出的对话框中，将目标变量添加到“因变量列表”框内。
点击“选项”按钮，然后在“统计”标签下勾选“置信区间”。默认情况下，置信区间为95%，用户可以根据需要更改置信水平。
点击“继续”和“确定”，SPSS将输出选定变量的置信区间。

2.2.2 输出结果的解读与注意事项
计算出的置信区间能够帮助我们了解统计量的估计精确度。例如，95%的置信区间意味着在多次重复抽样中，大约有95%的置信区间包含了总体参数的真实值。
输出结果的解读需要注意以下几个要点：

中心值：通常是均值或比例，表示估计的中心点。
置信限：表示置信区间的上下限，反映了估计的精确性。
置信水平：表示置信区间的可信度，常见的有95%和99%。

在使用置信区间时，需要注意样本量的大小、数据分布的形状以及潜在的抽样偏差等因素，这些都可能影响置信区间的准确性和解释。
2.3 SPSS在置信区间应用中的优势与局限
2.3.1 SPSS用户界面友好性分析
SPSS的用户界面设计遵循直观原则，新手用户可以无需阅读大量文档即开始使用。界面布局合理，常用功能按钮一目了然，且菜单选项逻辑清晰，便于用户根据统计需求找到对应的分析工具。
尽管如此，对于非统计专业的用户而言，理解统计分析的内部原理和结果的统计意义仍有一定挑战性。此外，SPSS的某些高级功能可能需要通过命令语法（Syntax）来实现，这对初学者而言可能不太友好。
2.3.2 SPSS在处理特定数据集的效率
SPSS在处理结构化数据和执行标准统计分析方面表现得相当出色，尤其是对于社会科学领域的大规模调查数据。在这些场景下，SPSS的高效性和强大的数据处理能力可以极大地简化研究者的工作量。
然而，当面对非结构化数