二相编码与多相编码综合比较:MATLAB仿真视角解析
发布时间: 2024-12-20 11:56:27 阅读量: 5 订阅数: 10 


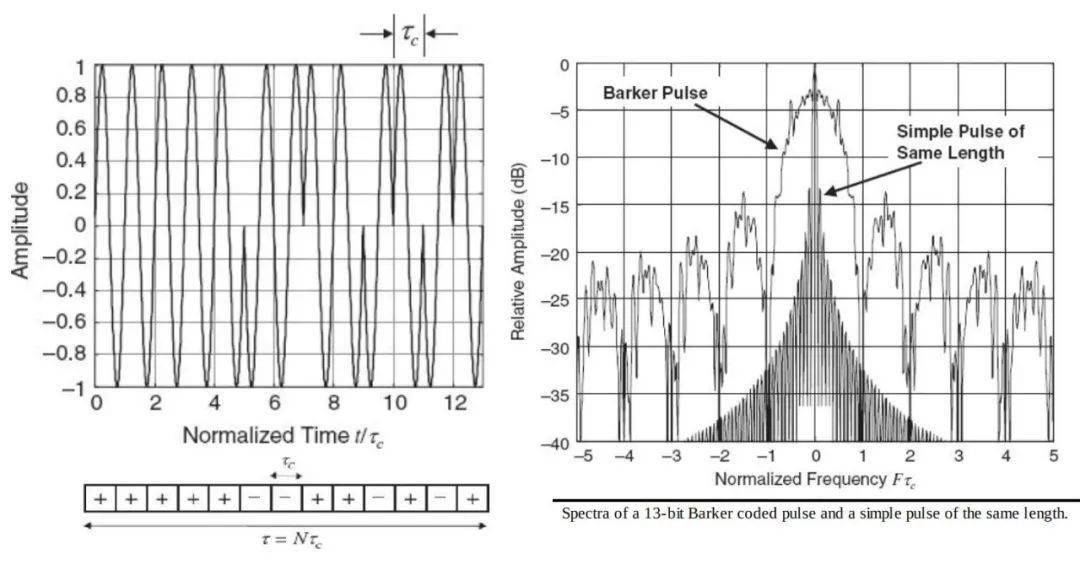
雷达二相编码和多相编码信号的matlab仿真研究
# 摘要
本论文旨在深入解析二相编码与多相编码的技术概念和原理,并通过MATLAB仿真环境对这两种编码技术进行对比分析。首先介绍了二相编码与多相编码的基本理论和数学模型,并探讨了它们在理论上的性能指标差异。接着,详细阐述了如何搭建MATLAB仿真环境,并准备相应的仿真实验案例。通过仿真实验,分析二相编码与多相编码在信号调制、解调及误码率方面的表现,并对结果进行了综合评价。最后,论文探讨了这些编码技术在现代通信领域的实际应用案例,并展望了编码技术在未来通信系统中的发展趋势,特别是与人工智能技术融合的可能性。
# 关键字
二相编码;多相编码;MATLAB仿真;信号调制;误码率分析;通信技术应用
参考资源链接:[Matlab仿真研究:二相编码与多相编码在雷达信号中的应用](https://wenku.csdn.net/doc/6412b7a4be7fbd1778d4b054?spm=1055.2635.3001.10343)
# 1. 二相编码与多相编码概念解析
## 1.1 编码技术的基本概念
编码技术是通信领域中用于提高数据传输效率、增强信号抗干扰能力的重要手段。在不同的应用场景中,编码技术表现出不同的特性与优势。理解编码技术的基本概念,对于深入探讨其在现代通信中的应用至关重要。
## 1.2 二相编码的特点
二相编码,又称为双相编码,是一种信号编码方式,它通过改变信号的相位来表示二进制的0和1。这种编码方式因其简单性和相对较高的传输速率,在早期的数字通信系统中被广泛采用。
## 1.3 多相编码的优势
多相编码则是在二相编码的基础上发展起来的,它使用了多个相位来编码数据,使得系统能够同时传输更多的信息。这种方法在带宽效率和信号功率谱密度方面通常表现更佳,尤其适合于现代高速数据传输的需求。
通过对比二相编码与多相编码,我们可以进一步探索编码技术的深层特性,并为优化通信系统的设计提供理论基础。接下来的章节将详细介绍这两种编码技术的理论基础和仿真实现。
# 2. 理论基础与编码原理
### 2.1 二相编码技术原理
#### 2.1.1 二相编码的定义与发展
二相编码,又称为双相编码(Biphase Encoding),是数字通信中的一种调制技术。二相编码的主要目的是为了确保数据传输的同步,并具有良好的抗干扰性能。其基本思想是用两个不同相位的信号元素来表示数字“0”和“1”。在二相编码中,可以是相位差180度的两种波形来代表二进制的两个逻辑状态,例如,一种是相位保持不变(代表逻辑“0”),另一种是相位反转(代表逻辑“1”)。
二相编码技术的发展可以追溯到早期的数字通信系统,当时是为了在传输中提供时间基准,确保接收端能够正确地解码发送的数据。随着技术的发展,二相编码被广泛应用于多种通信协议中,如曼彻斯特编码和差分曼彻斯特编码等。它们虽然都属于二相编码的范畴,但在具体实现上有所不同,有着各自的优点和应用场景。
#### 2.1.2 二相编码的数学模型
二相编码的数学模型可以基于傅里叶变换来分析。在理想情况下,如果一个二相编码系统使用了正弦波形,那么编码后的信号可以表示为一个连续的正弦波序列。信号的相位在每个比特周期的中间点发生跳变,根据比特值的不同而有不同的跳变规律。因此,二相编码的信号可以表示为:
```
s(t) = A * cos(ωt + φ(n)) for 0 ≤ t < T/2, n = 0
s(t) = A * cos(ωt + φ(n) + π) for T/2 ≤ t < T, n = 1
```
其中,`A`是振幅,`ω`是角频率,`T`是比特周期,`φ(n)`是第`n`个比特周期开始时的初始相位,`φ(n)`在连续的比特周期中是恒定的,但每次比特值变化时它会加上或减去`π`(即180度相位跳变)。
### 2.2 多相编码技术原理
#### 2.2.1 多相编码的定义与发展
多相编码(M-ary Phase Shift Keying, M-PSK)是数字通信中的一种调制方式,它将二进制数据映射到具有多个相位的信号上。常见的多相编码方式包括二相编码(即BPSK),四相编码(QPSK),八相编码(8-PSK)等。多相编码技术可以提供比二相编码更高的数据传输速率,因为它可以利用相位的不同状态来传输更多的信息。
多相编码技术的发展与无线通信技术的进步密切相关。随着无线频谱资源日益紧张,需要更高效的数据传输方式来提高频谱利用率。多相编码技术便是在这样的背景下得到了快速的发展和应用。特别是在卫星通信和移动通信中,多相编码技术的应用显著提升了通信系统的性能。
#### 2.2.2 多相编码的数学模型
多相编码的数学模型较二相编码更为复杂,因为它涉及到多个相位的状态。以QPSK为例,信号的相位可以是0度、90度、180度、270度四种状态,它们可以分别代表两个比特的不同组合(00、01、10、11)。数学上,QPSK信号可以表示为:
```
s(t) = A * cos(ωt + φ) if bit1 = 0 and bit2 = 0
s(t) = A * cos(ωt + φ + π/2) if bit1 = 1 and bit2 = 0
s(t) = A * cos(ωt + φ + π) if bit1 = 1 and bit2 = 1
s(t) = A * cos(ωt + φ + 3π/2) if bit1 = 0 and bit2 = 1
```
其中,`A`是振幅,`ω`是角频率,`φ`是初始相位,`bit1`和`bit2`代表两个比特位。
### 2.3 二相编码与多相编码的理论对比
#### 2.3.1 码元速率与带宽效率
二相编码和多相编码在码元速率和带宽效率方面存在显著差异。二相编码因为每个码元只有两个可能的状态,所以其码元速率较高。相对地,多相编码每个码元能够表示更多的信息位,因此在同等条件下,多相编码可以提供更高的数据传输速率。
但是,多相编码由于其相位状态的增加,在相位调制时需要更高的频率分辨率,进而影响到其带宽效率。此外,多相编码的信号更容易受到相位噪声的影响,这要求在设计多相编码系统时需要更精准的同步和更复杂的信号处理技术来保证性能。
#### 2.3.2 信号的功率谱分析
在信号的功率谱分析中,二相编码和多相编码显示出不同的特性。二相编码因为其恒定的包络特性,使得其功率谱较为集中,且在频带边缘的滚降率较快,这有助于抑制带外辐射,减少干扰。多相编码的功率谱通常更宽,并且由于其包络波动,使得其对放大器的线性要求较高,否则容易产生非线性失真,导致信号失真和频谱扩展。
为了更精确地分析二相编码和多相编码的功率谱特性,我们可以采用MATLAB软件进行仿真。下面是基于MATLAB的仿真代码示例:
```matlab
% 二相编码信号的功率谱仿真
t = (0:1/1000:1).'; % 采样时间向量
N = length(t); % 采样点数
data = randi([0 1], 1, N); % 随机生成二进制数据
biphase_signal = biphase_encode(data); % 二相编码信号
% 计算并绘制功率谱密度
[Pxx, f] = pwelch(biphase_signal, [], [], N, 1000);
plot(f, 10*log10(Pxx));
title('二相编码信号的功率谱密度');
xlabel('频率 (Hz)');
ylabel('功率/频率 (dB/Hz)');
% 多相编码信号的功率谱仿真(以QPSK为例)
qpsk_signal = qpsk_encode(data); % QPSK编码信号
[Pxx, f] = pwelch(qpsk_signal, [], [], N, 1000);
plot(f, 10*log10(Pxx));
title('QPSK编码信号的功率谱密度');
xlabel('频率 (Hz)');
ylabel('功率/频率 (dB/Hz)');
function encoded_signal = biphase_encode(data)
% 二相编码信号的生成函数
% 这里省略具体编码细节
end
function encoded_signal = qpsk_encode(data)
% QPSK编码信号的生成函数
% 这里省略具体编码细节
end
```
在这段代码中,我们使用了`pwelch`函数来计算信号的功率谱密度。通过比较不同编码方式的功率谱,我们可以看到二相编码与多相编码在信号传输效率和频谱使用方面的差异。请注意,上述代码中的`biphase_encode`和`qpsk_encode`函数需要根据具体的编码算法进行实现。
# 3. MATLAB仿真环境搭建
## 3.1 MATLAB基础与仿真工具箱
### 3.1.1 MATLAB软件概述
MATLAB是一种高性能的数值计算和可视化软件,广泛应用于工程计算、算法开发、数据分析和可视化等多个领域。它提供了一个交互式环境,以及一系列内置函数和工具箱,使得复杂算法的实现变得简单快捷。对于通信工程师而言,MATLAB不仅能够提供强大的仿真工具箱,还可以帮助开发者在设计和测试阶段对通信系统进行深入研究。
### 3.1.2 通信系统工具箱介绍
通信系统工具箱是MATLAB众多工具
0
0





