数字逻辑难点突破：第五版进阶学习者的必备指南


# 摘要
本文旨在系统复习数字逻辑基础，并深入探讨进阶数字逻辑理论，包括优化设计、状态机设计、时序分析等关键议题。通过对数字电路的逻辑简化、电路最小化、时序电路工作原理以及时钟域交叉等问题的分析，文章进一步阐述了逻辑仿真工具的使用、设计验证与故障分析以及测试向量生成的重要性。此外，本文还涵盖了数字逻辑实战项目的规划、实施、验证和总结，以及数字逻辑中的新技术如量子计算、FPGA技术和AI的交叉应用。最后，本文推荐了优质的学习资源和社区，为数字逻辑学习者提供全面的学习路径和交流平台。本文的目的是为读者提供一个全面、深入的数字逻辑知识框架，并指向实践应用和未来研究方向。

# 关键字
数字逻辑；电路优化；状态机设计；时序分析；逻辑仿真；量子计算；FPGA技术；人工智能；学习资源

参考资源链接：[欧阳星明《数字逻辑》课后答案详解：模拟与数字信号，电路分类](https://wenku.csdn.net/doc/1tmgj24acv?spm=1055.2635.3001.10343)
# 1. 数字逻辑基础复习

数字逻辑是计算机和电子系统设计的基础，它涉及了信号、电路和系统的设计与分析。在这一章节中，我们将快速回顾数字逻辑的关键概念。

## 1.1 二进制数和逻辑门基础

在数字逻辑领域，二进制数是最基础的表示方法，每个位（bit）要么是0要么是1。这种简单的表示法是构建更复杂电路的基石。

graph TD;
A[二进制数] --> B[0]
A --> C[1]

- **逻辑门** 是数字电路的基本单元，负责执行布尔逻辑运算。例如，AND门只在两个输入都是1时输出1。
- **非门（NOT）** 将输入信号取反。
- **或门（OR）** 在任一输入为1时输出1。
- **与门（AND）** 只在两个输入都为1时输出1。
- **异或门（XOR）** 当输入不同时输出1。

这些基础逻辑门构成了更复杂数字系统的骨架，它们之间的组合可实现各种逻辑功能。

## 1.2 逻辑表达式和真值表

**逻辑表达式** 是描述逻辑门如何根据输入信号组合输出结果的一种数学表示法。例如，\(A \land B\) 表示 A 和 B 的逻辑与。

graph TD;
A[逻辑表达式] --> B[与 (AND)]
A --> C[或 (OR)]
A --> D[非 (NOT)]
A --> E[异或 (XOR)]

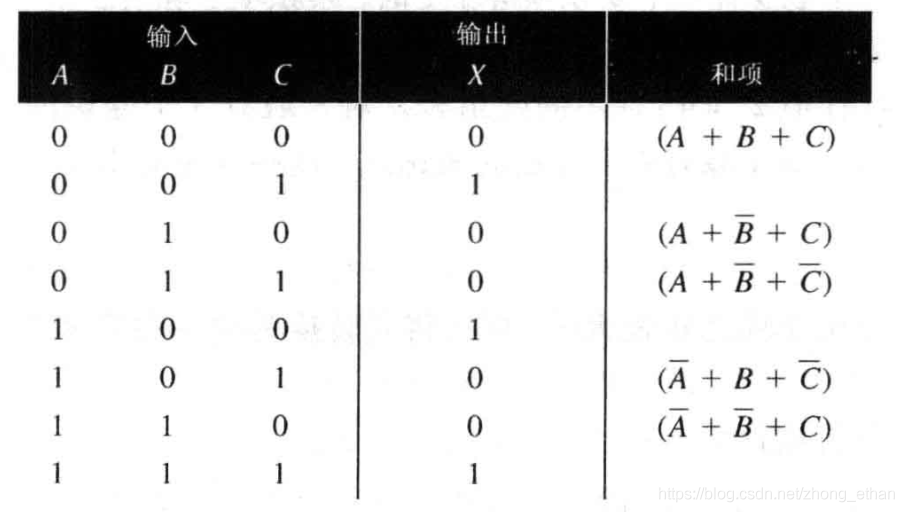
- **真值表** 是列出所有可能输入组合及其对应输出结果的表格。它展示了逻辑表达式的完整行为。

通过掌握逻辑门和逻辑表达式，我们能够构建和理解更高级的数字逻辑结构。这一基础复习将为后续章节中关于优化设计、状态机和时序分析的讨论打下坚实的基础。

# 2. 进阶数字逻辑理论详解

数字逻辑是现代电子设计的基石，随着技术的进步，我们对数字逻辑设计的理解需要不断深化。本章节深入探讨了进阶数字逻辑理论的多个方面，包括数字电路的优化设计、状态机与同步设计、以及数字逻辑中的时序分析。这些内容是数字逻辑设计者在面对复杂系统设计时必须掌握的核心概念。

## 2.1 数字电路的优化设计

数字电路设计的目标是实现既定的逻辑功能，同时达到性能最优、功耗最低、成本最低。优化设计是一个综合考量上述因素的过程，其中涉及的技术和方法很多，本节将重点介绍逻辑简化技术以及电路最小化的方法。

### 2.1.1 逻辑简化技术

在数字逻辑设计中，逻辑简化是最基本的优化步骤之一。它旨在减少组成电路的逻辑门数量，从而降低设计的复杂度和成本。逻辑简化技术的关键在于找到等价的逻辑表达式，这些表达式能用更少的逻辑门实现相同的功能。

最常用的逻辑简化方法是卡诺图（Karnaugh Map，K-map），它通过图形化的方式直观显示逻辑函数中变量之间的关系。通过合并相邻的1或0，可以得到最简逻辑表达式。

graph TD;
    A[卡诺图表示] --> B[1圈表示的项]
    B --> C[尽可能大的圈合并]
    C --> D[每个圈至少包含两个1]
    D --> E[相邻圈合并以减少圈的数量]
    E --> F[得到最简表达式]

在使用卡诺图进行逻辑简化时，需要注意以下几点：
1. 每个圈至少包含2的幂次个1（如2, 4, 8等），以便于合并简化。
2. 尽可能将1圈合并，以减少圈的数量。
3. 对于卡诺图中只有一个1的格子，可以使用“补0法”，即添加一个不存在的变量，这个变量在当前格子为0，其余为1。

### 2.1.2 电路的最小化

除了卡诺图，还可以使用奎因-麦克拉斯基（Quine-McCluskey）方法或者代数法进行电路最小化。这些方法虽然较为复杂，但能处理的逻辑变量数目较多，适合自动化工具实现。

代数法基于逻辑代数的规则，对逻辑表达式进行变换，消去冗余项。例如，利用德摩根定律、分配律和结合律等基本逻辑恒等式，可以对表达式进行重组，得到更简洁的等效表达式。

原始表达式: F = AB + BC
应用分配律: F = B(A + C)
简化结果: F = B

## 2.2 状态机与同步设计

在数字系统中，状态机是处理序列化事件和条件逻辑的重要组成部分。根据不同的要求，状态机可以是同步的也可以是异步的。理解这两者的差异对于设计高质量的数字系统至关重要。

### 2.2.1 有限状态机的概念和应用

有限状态机（Finite State Machine, FSM）由有限个状态、转移条件和输出动作组成。在任何给定的时间点，状态机都处于一个特定的状态，并根据输入信号进行状态转移。状态机广泛应用于各种数字系统，如处理器、存储控制器和通信协议中。

FSM 可以分为两大类：确定性有限状态机（Deterministic FSM，DFSM）和非确定性有限状态机（Nondeterministic FSM，NDFSM）。DFSM 中每个状态和输入的组合都有一个唯一的后继状态；而NDFSM则可能存在多个后继状态或没有后继状态。

在设计FSM时，状态分配至关重要，需要考虑到以下几点：
- 确保状态分配能够减少状态转移的复杂性。
- 尽可能使用二进制编码，以减少组合逻辑的复杂度。
- 避免相邻状态之间只有一个状态位变化，这可能会减少电路的抗干扰能力。

### 2.2.2 同步与异步状态机的区别

同步状态机的时钟信号是统一的，所有状态转移发生在时钟边沿的瞬间。这种设计可以更容易地满足时序要求，因为所有的逻辑动作都是在时钟控制下同步进行的。然而，同步设计对于时钟信号的质量和分布提出了较高的要求。

异步状态机不依赖于统一的时钟信号，其状态转移由输入信号的到达和稳定直接触发。异步状态机能够更好地处理快速事件，但设计复杂度较高，且容易受到信号传播延迟的影响，产生竞争和冒险问题。

graph TD;
    A[状态机类型] --> B[同步状态机]
    A --> C[异步状态机]
    B --> D[时钟边沿触发]
    C --> E[输入信号触发]
    D --> F[设计简单、时序容易控制]
    E --> G[响应快速、但设计复杂]
    F --> H[时钟信号质量要求高]
    G --> I[避免竞争和冒险]

## 2.3 数字逻辑中的时序分析

时序分析是数字逻辑设计的核心环节，它保证系统在不同的工作条件下依然能够可靠地运行。时序电路依赖于时钟信号，因此其分析和设计要比组合逻辑更为复杂。

### 2.3.1 时序电路的工作原理

时序电路包含存储元件（如触发器），能够记忆状态信息。触发器通过时钟信号的边沿将输入信号存储为状态，这些状态在下一个时钟边沿到来之前保持