深入理解闭环控制的精髓：STM32 PID控制算法详解

# 1. 闭环控制的基础理论

闭环控制是一种反馈控制系统，它通过测量系统输出并将其与期望输出进行比较来控制系统。该比较产生的误差信号被用来调整系统输入，从而将输出保持在期望值附近。

闭环控制系统由三个主要组件组成：传感器、控制器和执行器。传感器测量系统输出并将其转换为电信号。控制器比较传感器信号和期望值，并产生一个误差信号。执行器接收误差信号并将其转换为系统输入的变化。

闭环控制系统可以提供比开环控制系统更好的精度和稳定性。这是因为闭环系统能够检测和纠正输出中的任何偏差。

# 2. PID控制算法的原理和设计

### 2.1 PID算法的数学模型

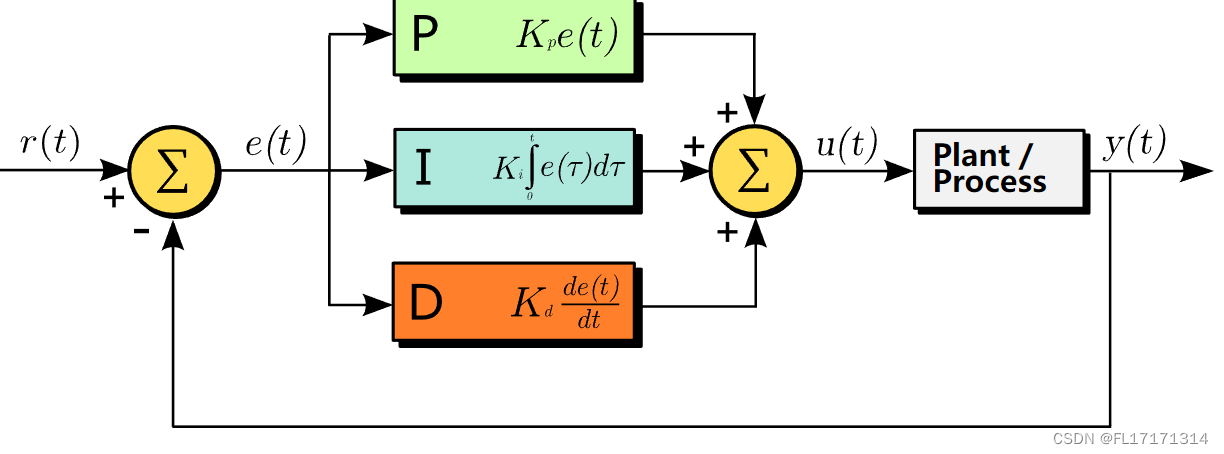
PID控制算法是一种反馈控制算法，其基本原理是根据偏差（误差）信号的比例、积分和微分项来计算控制输出。PID算法的数学模型如下：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* `u(t)` 为控制输出
* `e(t)` 为偏差信号（误差）
* `Kp` 为比例增益
* `Ki` 为积分增益
* `Kd` 为微分增益

#### 2.1.1 比例项（P）

比例项（P）根据偏差信号的当前值进行控制。其作用是快速响应偏差，减少稳态误差。比例增益`Kp`越大，响应越快，但稳定性越差。

#### 2.1.2 积分项（I）

积分项（I）根据偏差信号的过去值进行控制。其作用是消除稳态误差，提高控制精度。积分增益`Ki`越大，稳态误差越小，但响应速度越慢。

#### 2.1.3 微分项（D）

微分项（D）根据偏差信号的变化率进行控制。其作用是预测偏差的变化，提高控制稳定性。微分增益`Kd`越大，稳定性越好，但响应速度越慢。

### 2.2 PID算法的参数整定

PID算法的参数整定至关重要，直接影响控制系统的性能。常见的参数整定方法有：

#### 2.2.1 Ziegler-Nichols方法

Ziegler-Nichols方法是一种基于阶跃响应的经验公式法。其步骤如下：

1. 将PID算法的积分和微分增益设置为0，即`Ki = 0`、`Kd = 0`。
2. 施加一个阶跃输入信号，观察系统响应。
3. 记录系统响应的上升时间`Tu`和峰值时间`Tp`。
4. 根据`Tu`和`Tp`，计算PID算法的增益参数：

Kp = 0.6 * Tu / Tp
Ki = 1.2 * Kp / Tp
Kd = 0.075 * Kp * Tp

#### 2.2.2 阶跃响应法

阶跃响应法是一种基于阶跃响应的试错法。其步骤如下：

1. 施加一个阶跃输入信号，观察系统响应。
2. 根据系统响应的过冲量、上升时间和稳定时间，调整PID算法的增益参数。
3. 重复步骤1和2，直到系统响应达到满意的效果。

#### 2.2.3 频率响应法

频率响应法是一种基于频率响应的分析法。其步骤如下：

1. 对系统施加一个正弦输入信号，并测量系统输出的幅值和相位响应。
2. 根据系统频率响应的增益裕度和相位裕度，调整PID算法的增益参数。
3. 重复步骤1和2，直到系统频率响应达到满意的效果。

# 3.1 STM32的硬件架构和外设

#### 3.1.1 微控制器架构

STM32微控制器基于ARM Cortex-M内核，具有以下特点：

- 高性能：主频高达168MHz，浮点运算单元（FPU）
- 低功耗：多种低功耗模式，包括睡眠、停止和待机模式
- 丰富的外设：包括定时器、ADC、DAC、UART、SPI、I2C等
- 内置存储器：包括Flash、SRAM和EEPROM

STM32微控