【提升SATSCAN分析精度】：数据预处理与质量控制的专业指南


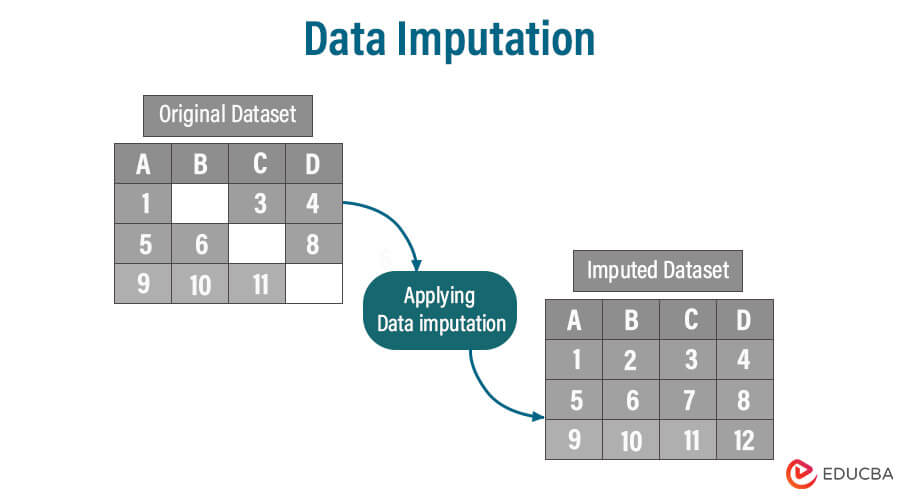
# 摘要
SATSCAN分析是一种空间统计方法，广泛用于探测地理信息系统（GIS）中的疾病聚集现象。本文重点阐述了数据预处理的重要性以及提高SATSCAN分析精度的策略。文章详细介绍了数据预处理的理论基础，包括数据收集、清洗、变换、归一化以及降维技术。同时，探讨了质量控制在数据分析中的理论与实践，包括一致性、完整性检查以及异常值处理。本文还分析了在SATSCAN分析中实施质量控制的方法，误差分析、模型验证及结果解释，并通过实际案例研究展现了数据预处理与质量控制在提升SATSCAN分析精度中的应用。最后，文章展望了SATSCAN分析技术未来的发展趋势，以及其在不同领域的扩展潜力和所面临的数据隐私与伦理问题。

# 关键字
SATSCAN分析；数据预处理；质量控制；异常值处理；模型验证；跨学科研究

参考资源链接：[SaTScan软件：空间时间统计分析工具](https://wenku.csdn.net/doc/6412b76fbe7fbd1778d4a4a0?spm=1055.2635.3001.10343)
# 1. SATSCAN分析与数据预处理的重要性

在现代数据分析和统计软件中，SATSCAN分析作为一种时空数据分析工具，特别在处理时空数据集时展示出其卓越的功能。但在深入探讨SATSCAN分析之前，我们必须先了解数据预处理的重要性。数据预处理是数据分析和挖掘流程中一个至关重要的环节，它直接影响到后续分析的准确性和可靠性。良好的数据预处理能够最大限度地减少噪音和异常值对分析结果的影响，确保数据分析模型能在理想状态下运行。在本章中，我们将探讨为什么SATSCAN分析需要重视数据预处理，以及数据预处理如何影响最终分析的结果。

## 2.1 数据收集与清洗

### 2.1.1 数据收集的方法和要点

数据收集是数据预处理的第一步，而在这个阶段的关键是选择合适的数据收集方法，并确保所收集的数据能够有效代表研究问题。数据收集方法可以是手动的，如问卷调查或观察，也可以是通过各种在线和离线渠道进行的数据抓取。要点包括确定数据来源的可靠性和一致性，以及收集数据时对隐私和安全的关注。

# 示例代码：使用Python进行简单的网页数据抓取
import requests
from bs4 import BeautifulSoup

url = 'http://example.com/data'
response = requests.get(url)
soup = BeautifulSoup(response.content, 'html.parser')
data = []
for item in soup.find_all('target_tag'):
    data.append(item.text)

### 2.1.2 数据清洗技术与策略

数据清洗的目的是识别和修正或删除数据集中的错误和不一致性。这包括处理缺失值、修正格式错误、去除重复记录等。采用适当的数据清洗技术可以大大提升数据分析的效率和质量。策略上，数据清洗通常包括自动化清洗和手动审查两个阶段。

# 示例代码：使用Pandas库处理缺失值
import pandas as pd

df = pd.read_csv('data.csv')
df.fillna(method='ffill', inplace=True)  # 前向填充缺失值

## 2.2 数据变换与归一化

### 2.2.1 数据变换的必要性与方法

数据变换是将原始数据转换为适合分析的形式。这可能包括将分类数据转换为数值形式、数据聚合、以及应用数学函数等。数据变换的必要性在于它能够改善模型性能，并且有助于后续的数据解释。

### 2.2.2 归一化处理的目的与实施步骤

归一化处理是调整数据范围至同一尺度的过程，其主要目的是消除不同特征间的量纲影响，保证各特征在分析模型中具有相同的权重。在实施归一化之前，必须先理解数据分布，选择合适的归一化方法，如最小-最大归一化或z-score标准化。

# 示例代码：使用sklearn库对特征进行z-score标准化处理
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X = scaler.fit_transform(X)  # X是一个特征矩阵

## 2.3 数据降维技术

### 2.3.1 主成分分析（PCA）原理与应用

主成分分析（PCA）是一种常用的数据降维技术，其核心思想是通过线性变换将数据映射到较低维度的子空间中，同时保留数据的主要信息。PCA在数据可视化和噪声过滤方面表现尤为突出。

### 2.3.2 其他降维技术概述

除了PCA，还有诸如线性判别分析（LDA）和t-SNE等降维技术。每种方法都有其特点和适用场景，比如t-SNE特别适合高维数据的可视化。选择合适的降维技术，能有效提升数据分析的可解释性和模型的预测精度。

# 示例代码：使用PCA进行数据降维
from sklearn.decomposition import PCA

pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X)  # X是需要降维的特征矩阵

本文的剩余章节将继续深入探索数据预处理的不同方面，并讨论如何应用这些理论和技术于SATSCAN分析中，以及如何通过质量控制方法提升分析精度。

# 2. 数据预处理的理论基础

### 2.1 数据收集与清洗
#### 2.1.1 数据收集的方法和要点
在数据分析的初期阶段，数据收集是一个至关重要的步骤。正确的方法和要点可以帮助我们收集到高质量、符合研究目的的数据。数据收集可以分为两种主要类型：一手数据收集和二手数据收集。一手数据通常指的是直接从源头获取的数据，例如通过调查问卷、实验观测等方式。而二手数据则是指已经存在并被收集过的数据，比如公开的数据库、政府发布的统计资料等。

数据收集需要关注的要点包括：
1. **目的性**：明确数据收集的目标，为后续分析工作定位。
2. **全面性**：确保数据覆盖所有相关的变量，避免重要信息的遗漏。
3. **准确性**：收集的数据需要真实可靠，误差应尽可能减小。
4. **时效性**：收集的数据应该反映当前的情况，以保持分析结果的时效性。

为了实现上述目标，可以使用多种工具和技术，例如：
- **在线调查工具**（如SurveyMonkey或Google表单）来设计问卷并收集数据。
- **APIs**（应用程序接口）用来从各种在线服务中抓取数据。
- **爬虫技术**以自动化的方式从网站上提取信息。

#### 2.1.2 数据清洗技术与策略
数据清洗是识别并处理数据集中不一致、错误、重复或不完整数据的过程。这个步骤能够显著提高数据分析的准确性和可靠性。数据清洗的基本策略包括：

- **识别异常值**：通过统计测试、可视化图表或数据挖掘技术，找出数据集中的异常值或离群点。
- **处理缺失值**：对于缺失的数据，可以采用删除、填充、预测等多种方法。删除是最直接的方法，但可能会导致信息的大量丢失；而填充可以使用均值、中位数、众数或基于模型的预测。
- **纠正错误**：当发现错误数据时，应该根据数据的来源和性质采取不同的修正方法。可能包括手动修正错误、使用数据清洗工具或编写自定义脚本来自动化修正过程。
- **统一格式**：确保所有数据遵循相同的格式，以消除由于格式不一致而导致的潜在错误。

下面是一个使用Python进行数据清洗的简单示例代码：

import pandas as pd

# 加载数据集
data = pd.read_csv('data.csv')

# 处理缺失值：填充
data.fillna(data.mean(), inplace=True)

# 处理异常值：例如，我们将年龄范围限制在18至65岁之间
data = data[(data['age'] >= 18) & (data['age'] <= 65)]

# 统一格式：将所有的日期数据转换为标准格式
data['date'] = pd.to_datetime(data['date'], format='%Y-%m-%d')

# 保存清洗后的数据
data.to_csv('clean_data.csv', index=False)

通过上述清洗步骤，数据集已经为后续分析做好了准备，提高了数据质量。

### 2.2 数据变换与归一化
#### 2.2.1 数据变换的必要性与方法
数据变换是指为了改进数据分布、增强模型性能、消除变量间的依赖性以及提高计算效率，而对数据进行一系列变换的过程。它包括但不限于数据缩放、离散化、变量转换等。

数据变换的必要性主要体现在以下几点：
- **提高模型的泛化能力**：通过数据变换可以减少模型对数据的敏感性，避免过拟合。
- **简化模型结构**：对数据进行变换可使模型结构更加简单，便于理解和解释。
- **提高计算效率**：适当的数据变换可以使算法的计算过程更加高效，特别是对于距离计算依赖型的算法。

常用的数据变换方法包括：
- **标准化（Standardization）**：将数据按比例缩放，使之落入一个小的特定区间，常用的是均值为0，标准差为1。
- **归一化（Normalization）**：将数据按比例缩放到一个范围，通常为0到1。
- **对数转换（Log Transformation）**：对数据进行对数变换，常用于处理具有重尾分布的数据。

例如，对于均值和标准差的标准化操作，可以使用如下公式：
\[ X' = \frac{X - \mu}{\sigma} \]
其中，\( X \) 是原始数据，\( \mu \) 是均值，\( \sigma \) 是标准差，\( X' \) 是标准化后的数据。

#### 2.2.2 归一化处理的目的与实施步骤
归一化处理的主要目的是使数据落入到一个具体的区间，通常是 [0, 1] 或 [-1, 1]。这样做的好处包括：
- **消除不同量纲的影响**：当数据由不同量纲或数量级时，归一化可以消除不同量纲的影响，使得模型更加关注数据的相对比例，而不是绝对值。
- **加快算法的收敛速度**：归一化后的数据可以加速很多算法的训练过程，特别是在使用基于梯度的优化方法时。

下面是一个Python中的归一化处理示例：

from sklearn.preprocessing import MinMaxScaler

# 加载数据
X = [[2100], [2200], [2300], [4000], [6000]]

# 初始化归一化对象
scaler = MinMaxScaler