【窗函数应用深度探究】：滑动平均滤波器的窗函数方法揭秘


# 摘要
窗函数方法在信号处理领域发挥着重要作用，其理论基础涉及数学定义、分类、特性以及在频域和时域中的应用。本论文首先介绍了窗函数的基本概念和在信号处理中的作用，然后详细阐述了窗函数在滑动平均滤波器设计中的应用，包括其对滤波器性能的影响和参数优化。进阶应用方面，讨论了多重窗函数技术及其优化策略，如降低旁瓣电平和增强主瓣宽度。最后，论文对窗函数应用的挑战进行了分析，并展望了该技术的未来发展趋势和在新兴领域的应用潜力。

# 关键字
窗函数方法；信号处理；滑动平均滤波器；频域分析；性能优化；数字信号处理软件

参考资源链接：[数字信号处理：滑动平均滤波器详解及特点](https://wenku.csdn.net/doc/78osurgcem?spm=1055.2635.3001.10343)
# 1. 窗函数方法简介

在数字信号处理领域，窗函数方法是一种重要的技术，它通过在信号的两端截取有限长度的信号段，来减少信号处理中出现的频谱泄漏问题。这种技术能够在时域内对信号进行局部化处理，从而在频域内对信号的频谱进行平滑和控制。

简单来说，窗函数就像是一副眼镜，能够帮助我们更清晰地观察信号的细节。通过选择合适的窗函数，我们可以根据信号处理的需求，优化时域和频域的性能，例如提高频率分辨率，减少旁瓣干扰，或实现更快的信号衰减。

本章将简要介绍窗函数方法的基本概念，并在后续章节中深入探讨其理论基础和应用，帮助读者更好地理解和掌握这一关键技术。

# 2. 窗函数的理论基础

## 2.1 窗函数的数学定义

### 2.1.1 窗函数的基本概念

在信号处理领域，窗函数是一种数学工具，它用于在时域上对信号进行截断和加权，以控制频域内频谱泄露和旁瓣电平。其基本形式是对一个无限长的信号进行截取，通过乘以一个有限长度的窗函数来实现。这种方法可以防止由于信号截断而产生的频谱泄露现象，从而改善信号的频域特性。

窗函数的概念可以简化为以下数学表达式：

设原始信号为 x(t)，窗函数为 w(t)，窗函数的长度为 T，窗函数截取的信号 x_w(t) 可以表示为：

x_w(t) = x(t) * w(t), 其中 0 <= t < T

通过应用窗函数，信号的频谱将会根据窗函数的类型呈现特定的形状和特性，例如矩形窗会产生最宽的主瓣但较高的旁瓣，而汉宁窗等具有更优的旁瓣抑制性能。

### 2.1.2 窗函数的分类与特性

窗函数按照其频域特性和时域形状，可以分为多种类型，如矩形窗、汉宁窗、汉明窗、布莱克曼窗等。每种窗函数都有其独特的优势和局限性，以及各自的数学表达式和频谱特性。

矩形窗：

矩形窗是最简单的窗函数形式，表达式如下：

w(t) = 1, 0 <= t < T

矩形窗在频域内表现为最宽的主瓣宽度，但同时伴随较高的旁瓣电平。在实际应用中，矩形窗可能在旁瓣引起的频率泄露上表现不佳。

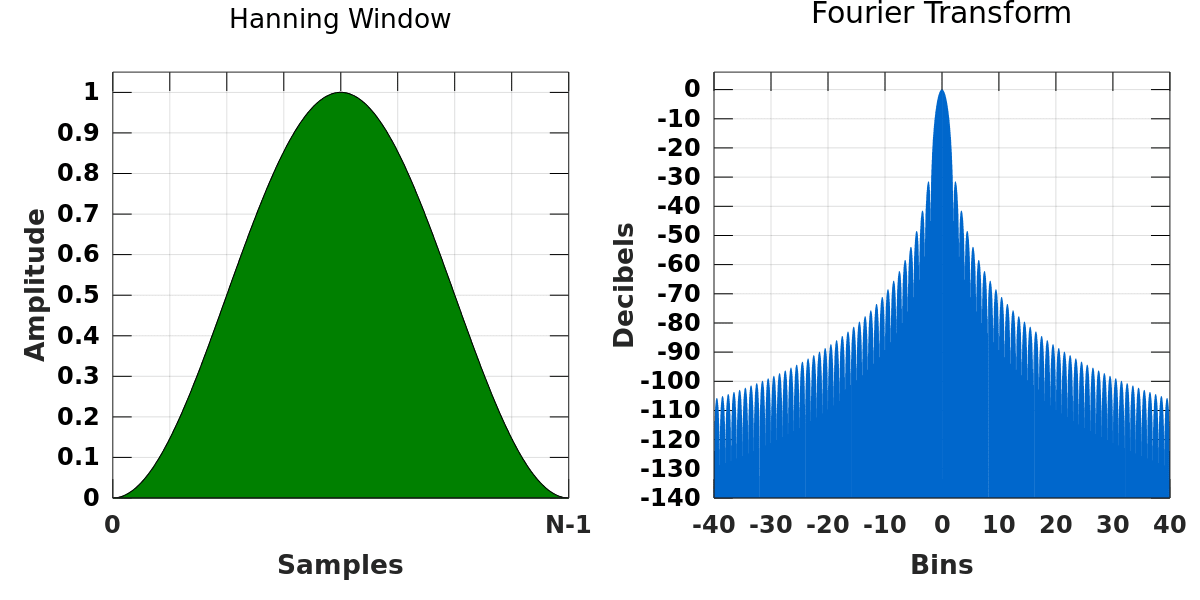
汉宁窗：

汉宁窗的表达式为：

w(t) = 0.5 - 0.5 * cos(2πt / T), 0 <= t < T

汉宁窗相比矩形窗在频域上的旁瓣电平更低，主瓣宽度较宽。在时域上，汉宁窗的过渡带宽度适中，是一种常用的窗函数。

上述窗函数只是其中的两个例子，实际上每种窗函数的设计都旨在在时域和频域之间找到一个合适的平衡点，以满足不同的应用需求。

## 2.2 窗函数在信号处理中的作用

### 2.2.1 频域分析中的窗函数应用

在频域分析中，窗函数的使用是为了获得信号频率成分的更准确估计。当处理有限长度的信号时，直接进行傅里叶变换会导致频谱泄露，即信号的实际频率成分会分散到相邻的频率上。窗函数通过在信号的两端逐渐减小到零的方式，可以减少这种泄露。

例如，在进行语音信号处理时，对一个语音帧应用窗函数，可以得到该帧信号的准确频率估计，从而进行更有效的编码或分析。

### 2.2.2 时域和频域分辨率的权衡

窗函数在改善频域泄露的同时，也会对信号的时域分辨率产生影响。例如，矩形窗具有最佳的时域分辨率，但其频域特性较差；而汉宁窗和其他更平滑的窗函数在频域有较好的抑制旁瓣的性能，却以牺牲时域分辨率为代价。

在实际应用中，需要根据信号的特定要求来选择窗函数，确保在时域和频域分析中取得最佳的权衡。例如，如果分析的信号包含快速变化的成分，可能需要选择具有更好时域分辨率的窗函数。

## 2.3 窗函数的选择原则

### 2.3.1 根据应用场景选择窗函数

在选择窗函数时，需要根据应用场景的具体需求来决定。例如：

- 如果信号的时域特性更重要，如在语音识别中，可以考虑使用时域分辨能力更强的窗函数。
- 如果信号的频域特性更重要，如在分析具有窄带干扰的信号时，应当选用频域泄露较少的窗函数。

### 2.3.2 常见窗函数的性能比较

不同窗函数在频域内具有不同的旁瓣抑制能力和主瓣宽度，以下是几种常见窗函数的性能比较：

- 矩形窗：主瓣最宽，旁瓣最高。
- 汉宁窗：较宽的主瓣，中等旁瓣电平。
- 汉明窗：更窄的主瓣，较低的旁瓣电平。
- 布莱克曼窗：非常窄的主瓣，最低的旁瓣电平，但过渡带较宽。

选择合适的窗函数，就是在这些窗函数的频域特性之间进行权衡，以适应不同的处理需求和性能要求。在实际应用中，通常需要进行实验和分析，以找到最佳的窗函数。

接下来的章节会继续探讨窗函数在滑动平均滤波器中的应用和优化策略。

# 3. 滑动平均滤波器的实现与应用

滑动平均滤波器（Moving Average Filter, MA Filter）是一种基本的低通滤波器，广泛应用于噪声过滤、数据平滑处理和趋势分析等领域。本章节将深入探讨滑动平均滤波器的工作原理，以及如何将窗函数应用于该滤波器来改善其性能。

## 3.1 滑动平均滤波器的基本原理

### 3.1.1 滑动平均滤波器的工作机制

滑动平均滤波器通过计算一系列连续数据点的平均值来过滤噪声。简言之，它将一组数据中的最新输入与前几个输入进行平均，以产生输出。此操作是一种简单而有效的线性滤波技术。

在实现滑动平均滤波器时，通常采用一个固定大小的数据窗口。数据窗口中的每个元素都会对最终的平均值产生影响，而每个新数据点都会使窗口滑动，从而更新平均值。滑动平均可以是简单滑动平均（Simple Moving Average, SMA）或加权滑动平均（Weighted Moving Average, WMA）。在SMA中，所有数据点权重相等；而在WMA中，更靠近