MATLAB取整指南：floor、ceil、round函数详解

# 1. MATLAB取整函数概述

MATLAB中提供了多种取整函数，用于将浮点数转换为整数。这些函数包括floor、ceil和round。取整函数的目的是将浮点数舍入到最接近的整数，并返回结果。

取整函数在数值计算中非常有用，例如四舍五入、控制小数点位数和舍入误差分析。它们还可以用于数据处理的优化和算法的应用。

# 2. 取整函数的理论基础

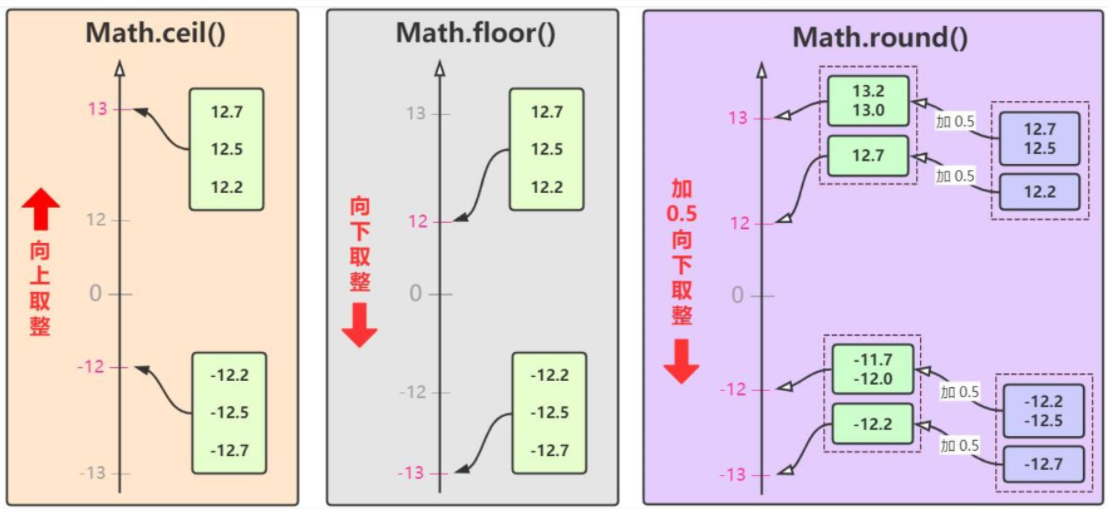
### 2.1 取整的概念和分类

**取整**是指将一个实数转换为一个整数的过程。取整函数根据其取整规则的不同，可以分为以下两类：

- **截断取整**：将实数的小数部分舍弃，得到一个不大于该实数的整数。
- **四舍五入取整**：将实数的小数部分四舍五入到最接近的整数。

### 2.2 取整函数的数学原理

**截断取整**的数学原理如下：

floor(x) = max{n ∈ Z | n ≤ x}

其中，`floor(x)`表示实数`x`的截断取整结果，`Z`表示整数集合。

**四舍五入取整**的数学原理如下：

round(x) = n，其中n是使得|x - n|最小的整数

其中，`round(x)`表示实数`x`的四舍五入取整结果。

**代码块：**

x = 3.14;
floor_result = floor(x);  % 截断取整
round_result = round(x);  % 四舍五入取整

disp(['截断取整结果：', num2str(floor_result)]);
disp(['四舍五入取整结果：', num2str(round_result)]);

**逻辑分析：**

上述代码中，`floor(x)`和`round(x)`分别对实数`x`进行了截断取整和四舍五入取整。`floor_result`和`round_result`分别存储了取整结果。

**参数说明：**

- `x`：要取整的实数
- `floor(x)`：`x`的截断取整结果
- `round(x)`：`x`的四舍五入取整结果

# 3. MATLAB取整函数的实践应用

### 3.1 floor函数的用法和实例

floor函数用于对浮点数进行向下取整，即将浮点数舍入到最接近的较小的整数。其语法格式为：

y = floor(x)

其中：

- `x`：输入的浮点数或浮点数数组。
- `y`：输出的向下取整后的整数或整数数组。

**实例：**

>> x = 3.14
>> y = floor(x)
y = 3

### 3.2 ceil函数的用法和实例

ceil函数用于对浮点数进行向上取整，即将浮点数舍入到最接近的较大的整数。其语法格式为：

y = ceil(x)

其中：

- `x`：输入的浮点数或浮点数数组。
- `y`：输出的向上取整后的整数或整数数组。

**实例：**

>> x = 3.14
>> y = ceil(x)
y = 4

### 3.3 round函数的用法和实例

round函数用于对浮点数进行四舍五入，即将浮点数舍入到最接近的整数。其语法格式为：

y = round(x)

其中：

- `x`：输入的浮点数或浮点数数组。
- `y`：输出的四舍五入后的整数或整数数组。

**实例：**

>> x = 3.14
>> y = round(x)
y = 3

**注意：**

当浮点数小数点后为0.5时，round函数会根据以下规则进行四舍五入：

- 如果浮点数为偶数，则舍入到偶数整数。
- 如果浮点数为奇数，则舍入到奇数整数。

**实例：**

>> x = 3.5
>> y = round(x)
y = 4

>> x = 4.5
>> y = round(x)
y = 4

# 4. 取整函数在数值计算中的应用

### 4.1 四舍五入的实现

四舍五入是将小数转换为整数时常用的方法。MATLAB 中没有专门的四舍五入函数，但可以通过取整函数组合实现四舍五入。

% 四舍五入到整数
x = 3.14159265;
y = round(x);
disp(y)  % 输出：3

% 四舍五入到小数点后两位
z = round(x, 2);
disp(z)  % 输出：3.14

### 4.2 小数点位数的控制

MATLAB 中的取整函数还可以用于控制小数点位数。

% 保留小数点后两位
x = 123.456789;
y = round(x, 2);
disp(y)  % 输出：123.46

% 保留小数点后零位
z = round(x, 0);
disp(z)  % 输出：123

### 4.3 舍入误差的分析

取整操作会引入舍入误差，即取整后的值与原始值之间的差值。舍入误差的大小取决于取整函数的类型和取整位数。

下表总结了不同取整函数的舍入误差：

| 函数 | 舍入误差 |
|---|---|
| floor | 总是负数 |
| ceil | 总是正数 |
| round | 正负交替 |

在数值计算中，需要考虑舍入误差的影响，尤其是当取整操作涉及大量数据时。

#### 代码示例

% 分析 floor 函数的舍入误差
x = [1.1, 1.5, 2.1, 2.5, 3.1];
y = floor(x);
error = x - y;
disp(error)  % 输出：[-0.1, -0.5, -0.1, -0.5, -0.1]

% 分析 ceil 函数的舍入误差
x = [1.1, 1.5, 2.1, 2.5, 3.1];
y = ceil(x);
error = x - y;
disp(error)  % 输出：[0.1, 0.5, 0.1, 0.5, 0.1]

% 分析 round 函数的舍入误差
x = [1.1, 1.5, 2.1, 2.5, 3.1];
y = round(x);
error = x - y;
disp(error)  % 输出：[0.1, 0.5, -0.1, -0.5, 0.1]

# 5. 取整函数的进阶技巧

### 5.1 取整函数的组合使用

取整函数可以组合使用，以实现更复杂的取整需求。例如，可以将 `floor` 函数和 `ceil` 函数结合起来，实现四舍六入五取偶。具体做法是：

x = 1.5;
y = floor(x + 0.5);  % 四舍六入五取偶

### 5.2 取整函数在数据处理中的优化

取整函数在数据处理中可以起到优化作用。例如，在对大数据进行统计分析时，可以先对数据进行取整，然后再进行计算。这样可以减少计算量，提高效率。

data = randn(1e6, 1);  % 产生100万个随机数
data_int = round(data);  % 对数据进行取整
mean_int = mean(data_int);  % 计算取整后数据的均值

### 5.3 取整函数在算法中的应用

取整函数在算法中也有广泛的应用。例如，在二分查找算法中，取整函数可以用来计算待查找元素在有序数组中的索引。

function index = binary_search(arr, target)
    low = 1;
    high = length(arr);
    while low <= high
        mid = floor((low + high) / 2);  % 取整计算中间索引
        if arr(mid) == target
            index = mid;
            break;
        elseif arr(mid) < target
            low = mid + 1;
        else
            high = mid - 1;
        end
    end
    if low > high
        index = -1;  % 未找到目标元素
    end
end