精通电阻网络计算：电压和电流的5大基本原理与方法


# 摘要
电阻网络是电路理论中的基础构件，对于理解和分析电路至关重要。本文首先概述了电阻网络的基础知识，然后深入探讨了其基本原理，包括欧姆定律、基尔霍夫定律以及等效电阻的计算方法。接着，本文详细阐述了电压与电流在电阻网络中的计算，重点分析了分压与分流原理以及超额定律和电桥平衡的应用。此外，本文介绍了多种电阻网络的分析方法，如网孔分析法、节点电压法及混合方法，并对其高级技巧进行了解读，包含非线性电阻和功率计算以及稳态与瞬态分析。最后，通过实际应用案例，展示了电阻网络在电路设计和故障诊断中的具体运用。本文旨在为读者提供一个全面理解电阻网络的框架，并强调其在工程实践中的实用价值。

# 关键字
电阻网络；欧姆定律；基尔霍夫定律；等效电阻；电压与电流计算；电路分析方法

参考资源链接：[倒T型电阻网络D/A转换器的工作原理与应用](https://wenku.csdn.net/doc/8577ysg86f?spm=1055.2635.3001.10343)
# 1. 电阻网络的基础知识概述

电阻网络是电子电路设计中的核心概念之一，它是由两个或多个电阻器通过一定的结构连接而成的网络系统。本章将简要介绍电阻网络的基础知识，为进一步深入探讨其原理和计算方法打下坚实的基础。

## 1.1 电阻网络的定义
电阻网络是由多个电阻组成，按照特定的方式连接在一起，以实现电压分配、电流分配或其他电子功能的电路结构。它可以是简单的串联和并联组合，也可以是复杂的多层网络。

## 1.2 电阻网络的重要性
在电子工程和电路分析中，电阻网络不仅用于计算电路中的电压、电流值，还广泛应用于信号处理、电源管理、传感器接口等领域。掌握电阻网络的基本知识对于电子工程师和电路设计师至关重要。

## 1.3 电阻网络的分类
电阻网络可以根据连接方式分为串联电阻网络、并联电阻网络以及更复杂的混联电阻网络。理解不同网络的分类有助于分析其行为和特性，从而进行有效的电路设计和优化。

电阻网络作为电路分析的基础，其功能和特性是后续章节深入探讨的核心，因此本章为读者提供了电阻网络的初步认识和重要性概述，为深入学习后续章节内容奠定了基础。

# 2. 电阻网络的基本原理

## 2.1 欧姆定律与电阻网络

### 2.1.1 欧姆定律的理论基础

欧姆定律是电阻网络分析的核心原理之一，它表明在一定温度下，通过一个导体的电流与该导体两端的电压成正比，与导体的电阻成反比。数学表达式为：V=IR，其中V表示电压（伏特），I表示电流（安培），R表示电阻（欧姆）。

欧姆定律不仅适用于单个电阻，还适用于由多个电阻构成的网络。在复杂网络中，不同路径上的电流和电压可能会有所不同，但每个电阻上的电压与电流的比值仍遵循欧姆定律。这一点为我们在分析电阻网络时提供了重要依据。

### 2.1.2 欧姆定律在电阻网络中的应用

在电阻网络中，我们经常需要计算不同节点间的电压差或是各支路的电流分配。应用欧姆定律可以帮助我们建立方程组，通过求解方程组来得到未知的电压或电流值。

例如，在一个含有多个电阻的串联网络中，欧姆定律允许我们用一个等效电阻R_eq来替换整个网络，并且能够简单地使用V=IR_eq来计算总电流。当网络更为复杂时，欧姆定律结合基尔霍夫定律为构建方程组提供了基础。

## 2.2 基尔霍夫定律

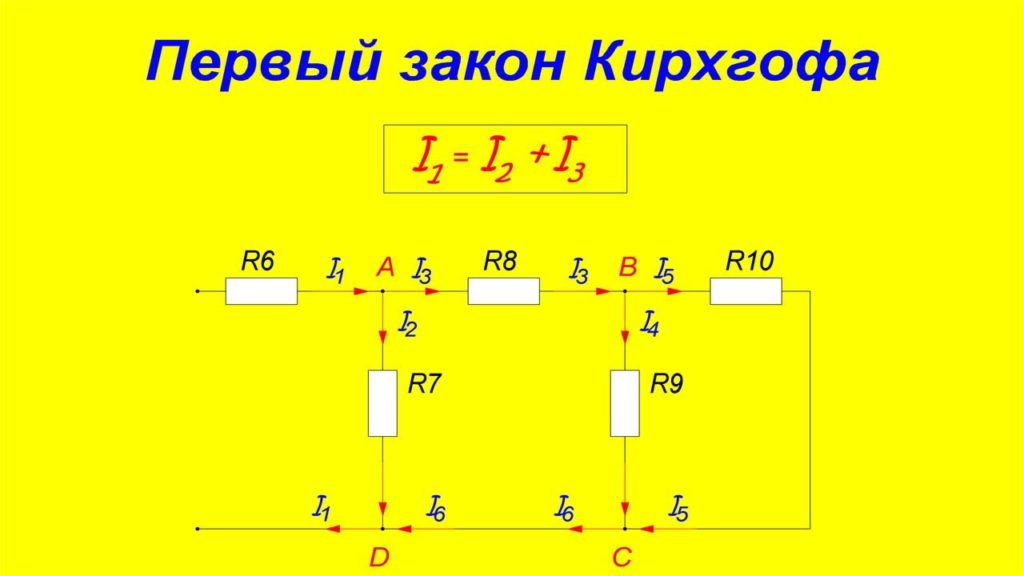
### 2.2.1 基尔霍夫电流定律(KCL)

基尔霍夫电流定律（KCL）表明在任何电路节点上，流入节点的电流总和等于流出节点的电流总和。KCL可以表示为：
\[ \sum_{k=1}^{n} I_k = 0 \]
其中，\(I_k\) 表示流入或流出节点的第k个电流。

在电阻网络中，应用KCL可以帮助我们确定节点间的电流关系，是电路分析中不可或缺的部分。例如，对于一个有三个分支流入和一个分支流出的节点，我们可以写成I1+I2+I3-I4=0。

### 2.2.2 基尔霍夫电压定律(KVL)

基尔霍夫电压定律（KVL）指出，在一个闭合回路中，沿着回路方向，电压的代数和等于零。数学表达式为：
\[ \sum_{j=1}^{m} V_j = 0 \]
其中，\(V_j\) 表示回路中第j个电压降。

在应用KVL时，必须注意电压降的方向。以顺时针方向为正方向，逆时针方向则为负方向。例如，对于一个包含电阻和电源的回路，我们可以将电压降和电源电压值代入KVL方程。

## 2.3 等效电阻的计算方法

### 2.3.1 串联和并联电阻的等效计算

串联和并联是电阻网络中最基本的连接方式，它们的等效电阻计算方法简单而重要。

串联电阻的等效电阻计算公式为：
\[ R_{eq} = R_1 + R_2 + ... + R_n \]

并联电阻的等效电阻计算公式为：
\[ \frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + ... + \frac{1}{R_n} \]

其中\(R_1, R_2, ..., R_n\)是组成网络的各个电阻值。

### 2.3.2 复杂网络的等效电阻求解技巧

对于更复杂的电阻网络，求解等效电阻通常涉及转换简化网络为只有单一串联或并联形式的等效模型。这通常需要运用欧姆定律、KCL和KVL，以及电阻串联并联的基本规则。

简化技巧包括：
- 提取公共节点，将网络简化为多电阻串联或并联。
- 应用Y-Δ变换，将某些复杂的电阻组合形式转换成更简单的形式。
- 使用节点分析法和网孔分析法来分别计算节点电压和网孔电流，从而求得等效电阻。

以下是Y-Δ变换的示例代码块，以阐释如何应用它来简化电阻网络：

def Y_to_Delta(Y11, Y12, Y22, Y33):
    # 假设Y11, Y12, Y22, Y33是Y形网络中对应电阻的电导值
    R1 = (Y11 * Y22 + Y11 * Y33 + Y22 * Y33) / Y12
    R2 = (Y11 * Y22 + Y11 * Y33 + Y22 * Y33) / Y12
    R3 = (Y11 * Y22 + Y11 * Y33 + Y22 * Y33) / Y12
    return R1, R2, R3

# 示例Y-Δ变换计算
Y11, Y12, Y22, Y33 = 1/10, 1/15, 1/15, 1/20
R1, R2, R3 = Y_to_Delta(Y11, Y12, Y22, Y33)
print("Δ形网络的电阻值为：", R1, R2, R3)

在该代码块中，我们定义了一个函数Y_to_Delta用于将Y形网络转换为等效的Δ形网络。然后，我们输入Y形网络的电导值，输出转换后的Δ形网络的电阻值。通过这一转换，复杂网络的等效电阻求解变得更加简单明了。

在下一节中，我们将继续探讨如何利用这些基本原理进行电压与电流的计算，以实现对电阻网络深入的理解。

# 3. 电阻网络中的电压与电流计算

电阻网络中的电压与电流计算是电路分析的核心内容之一。理解这些基本概念不仅可以帮助我们设计和分析电路，还能够让我们在遇到电路故障时迅速定位问题。本章将深入探讨电压分压与分流原理，以及超额定律与电桥平衡的应用。

## 3.1 电压分压与分流原理

电压分压和分流是电阻网络中普遍存在的现象，它们在电路设计和故障排除中起着至关重要的作用。

### 3.1.1 分压原理及其应用

分压原理是指在串联电路中，电压会按照电阻的比例分配。例如，两个串联的电阻R1和R2分别承载V1和V2的电压，那么总电压V等于V1加V2，且满足V1/V2 = R1/R2。

flowchart LR
A[电压源V] -->|R1| B[节点A]
B -->|R2| C[地]
A --> C

在上述示例中，如果R1和R2串联接入一个电压源V，那么节点A和地之间的电压将根据电阻值的不同而分配。

#### 分压原理的计算步骤

1. 确定电路中的总电压V和各个电阻的阻值。
2. 应用欧姆定律，计算出流过各个电阻的电流。
3. 使用欧姆定律，将电流与各个电阻值相乘，计算出各自的电压降。
4. 最后，根据电路的具体连接方式，找出需要计算的节点间电压。

### 3.1.2 分流原理及其应用

分流原理指的是在并联电路中，电流会按照电阻的倒数比例分配。在并联电阻网络中，如果R1和R2并联连接，它们共同承载电流I，流过R1和R2的电流分别为I1和I2，那么满足I1/I2 = R2/R1。

flowchart LR
A[电流源I] --> B[节点A]
A --> C[节点B]
B -->|R1| D[地]
C -->|R2| D

在该并联电路中，电流I被分配为I1和I2，分别流过R1和R2。

#### 分流原理的计算步骤

1. 确定电路中的总电流I和各个电阻的阻值。
2. 利用欧姆定律计算各个分支上的电压。
3. 应用欧姆定律和并联电路的特性，计算出流经各个电阻的电流。
4. 最终确定每个电阻上的电流分配情况。

## 3.2 超额定律与电桥平衡

超额定律和电桥平衡是更高级的电路分析方法，它们在精确测量电阻和设计精密电子设备中有着广泛的应用。

### 3.2.1 超额定律的理论和实践

超额定律是一个关于电桥电路的分析工具。它可以帮助我们理解当电桥平衡时，电桥的两边电位相等，因此流过检流计的电流为零。

flowchart LR
A[电压源V] -->|R1| B[节点A]
B -->|Rx| C[节点B]
A -->|R2| D[节点D]
D -->|R3| C
C --> E[检流计]

在这个电路中，当Rx满足R1/R2 = R3/Rx时，电桥达到平衡状态。

#### 超额定律的应用实例

超额定律的一个典型应用是在惠斯通电桥中测量未知电阻。当电桥平衡时，可以通过其他三个已知电阻的值来确定未知电阻Rx的值。

### 3.2.2 电桥平衡原理及其在测量中的应用

电桥平衡是电桥电路中的一个状态，此时通过电桥的两个分支的电位差为零，因此流过电桥中间的电流也为零。这可以用于精密测量电阻值，如使用惠斯通电桥或开尔文双电桥。

flowchart LR
A[电压源V] -->|R1| B[节点A]
B -->|Rx| C[节点B]
A -->|R2| D[节点D]
D -->|R3| C
C --> E[检流计]

在上面的电桥电路中，当电桥处于平衡状态时，可以通过调节Rx或R3的阻值使电位差为零。

#### 电桥平衡原理的计算步骤

1. 设置并测量电桥两端的电压。
2. 逐步改变未知电阻Rx或可变电阻R3，直至电桥达到平衡（检流计读数为零）。
3. 使用电桥平衡条件公式，通过已知电阻的值来解算未知电阻Rx。

在本章中，我们深入探讨了电阻网络中电压与电流的计算原理和方法。下一章将介绍电阻网络的分析方法，包括网孔分析法和节点电压法，它们为复杂电阻网络的分析提供了强有力的工具。

# 4. 电阻网络的分析方法

## 4.1 网孔分析法

### 4.1.1 网孔电流法的理论基础

网孔分析法是一种在复杂电路分析中应用广泛的计算方法，它的核心在于将电路中的每一个独立回路定义一个网孔电流。这种方法是基于基尔霍夫电压定律（KVL），通过应用KVL于每个网孔，可以得到一组方程。网孔电流法允许工程师避免处理电路中各个元件之间的相互作用，而是将注意力集中在网孔上，简化了分析过程。

每个网孔电流代表通过该网孔的电流假设路径。通过给定的网孔电流，可以求解电路中任意位置的电压和电流。假设每个网孔电流为一个未知数，然后使用KVL来建立方程组，通过解这些方程组即可求出网孔电流，进而确定电路中所有其他电压和电流。

### 4.1.2 网孔分析法的计算步骤与实例

网孔分析法的计算步骤如下：

1. 标识电路中的所有独立网孔，并为每个网孔定义一个网孔电流，通常用顺时针方向。
2. 应用KVL于每个网孔，列出方程。对于包含电源的网孔，电压源的方向需考虑其极性。
3. 将所有网孔方程组合成一个线性方程组。
4. 解这个线性方程组，求出网孔电流。
5. 使用网孔电流计算电路中其他未知量，如节点电压、分支电流等。

#### 例题解析

考虑以下电路：

      +V1
      /|
     / |
    /  |
   +---+---+ R1
   |    |
  R2   R3
   |    |
   +---+---+
      |
      V2

这里我们假设电路有两个网孔，因此会有两个网孔电流I1和I2。我们使用KVL对每个网孔建立方程：

对于网孔1：
V1 - R1 * I1 - R2 * (I1 - I2) = 0

对于网孔2：
R2 * (I2 - I1) - R3 * I2 - V2 = 0

解这个线性方程组，可以得到网孔电流I1和I2的值。然后通过I1和I2进一步求解电路中其他电压和电流。

## 4.2 节点电压法

### 4.2.1 节点电压法的原理解析

节点电压法，又称节点分析法，是另一种分析复杂电路的方法。它基于基尔霍夫电流定律（KCL），适用于计算电路节点之间的电压差。节点电压法通过选择节点并为每个节点分配一个电压值，然后建立一组基于这些节点电压的方程，来求解电路中的未知电压。

节点电压法的关键在于理解电流流入和流出节点的概念。电流流入节点时，相当于电流从参考点（通常是地线）流到该节点；电流流出节点时，相当于电流从该节点流向参考点。电流和电压之间的关系通过欧姆定律建立。

### 4.2.2 应用节点电压法解决复杂网络问题

应用节点电压法的步骤如下：

1. 标识电路的所有节点，并选择一个节点作为参考节点（通常为地线）。
2. 为每个非参考节点分配一个未知数作为节点电压。
3. 应用KCL于每个非参考节点，列出方程。注意电流源方向以及电流流入和流出节点的区别。
4. 将所有节点方程组合成一个线性方程组。
5. 解这个线性方程组，求出所有节点的电压。
6. 使用节点电压计算电路中其他未知量，如分支电流等。

#### 例题解析

假设有一个三个节点的电路，节点1连接到电源V1，节点2和节点3连接到电阻R1、R2和R3。我们要找节点2和节点3相对于节点1的电压。

使用KCL，我们可以为节点2和节点3建立方程：

节点2:
(V2 - V1)/R1 + (V2 - V3)/R2 = 0

节点3:
(V3 - V2)/R2 + (V3 - V1)/R3 = 0

其中，V2和V3是节点2和节点3相对于节点1的电压。通过解这个方程组，我们可以求出V2和V3，进一步可以计算出电路中其他各点的电压和电流。

## 4.3 混合方法与案例分析

### 4.3.1 结合网孔分析法和节点电压法

在某些电路分析中，单独使用网孔分析法或节点电压法可能不足以解决问题，或者计算过程过于复杂。混合方法，即结合使用网孔分析法和节点电压法，可以发挥两者的优势，从而更高效地解决复杂电路问题。通常情况下，这种结合方法特别适用于计算含有多重电源和电阻的电路。

### 4.3.2 复杂电路的混合方法应用实例

例如，考虑一个包含数个电源和复杂连接的电路。通过选择适当的节点和网孔，并为它们分别建立方程组，我们可以得到两个独立的线性方程系统。然后可以通过以下步骤结合这两个系统：

1. 将网孔方程和节点方程组并列。
2. 调整方程组，使得节点电压方程和网孔电流方程相互补充。
3. 重新组织方程组，消除重复变量。
4. 解这个结合后的方程组，求出所有未知的节点电压和网孔电流。
5. 计算电路中其他电压和电流值。

由于混合方法结合了两种分析方法的优点，因此在某些情况下可以减少未知量的数量，并简化整个分析过程。特别是当电路结构复杂，单独使用任一方法都很困难时，这种方法尤其有用。

经过上文对电阻网络的分析方法的介绍，我们可以看出，对于复杂电路的分析，选择合适的分析方法能够有效地简化问题，并得到所需的电路参数。通过上述的理论和应用实例，读者应该能够掌握网孔分析法、节点电压法以及它们的混合应用，为解决实际电路问题打下坚实的基础。

# 5. 电阻网络计算的高级技巧

## 5.1 非线性电阻与功率计算

### 5.1.1 非线性电阻特性的理解

非线性电阻是指电阻值随电压或电流的变化而变化的元件。这类电阻在电路中的行为更加复杂，因为其不能简单地使用欧姆定律（V=IR）来描述。常见的非线性电阻包括热敏电阻、光敏电阻和变阻器等。非线性电阻的伏安特性曲线通常是非线性的，意味着在电压和电流之间不存在一个固定的乘积关系。理解非线性电阻的特性对于分析包含此类元件的电阻网络至关重要。

在设计和分析含有非线性电阻的电路时，通常需要借助图表、模拟软件或非线性方程来获取更精确的结果。在实际应用中，非线性电阻可用于温度传感器、电流限制器、电压调节器等。

### 5.1.2 功率在电阻网络中的计算方法

在电阻网络中，功率的计算同样关键，尤其当涉及非线性电阻时。功率的计算公式为：

\[ P = V \times I \]

对于线性电阻，使用欧姆定律可以轻易地计算功率。然而，对于非线性电阻，必须使用实际测量或已知的非线性关系来计算功率。功率计算的准确性对于电路设计的效率和可靠性至关重要。

例如，在电路设计中，需要估算非线性负载下的功率耗散，以确保散热措施足够，并避免过热。在功率控制电路中，非线性电阻可以用来降低通过某些敏感组件的功率，从而保护这些组件免受损坏。

## 5.2 稳态与瞬态分析

### 5.2.1 电阻网络的稳态分析

稳态分析是在电路达到稳定工作状态后的性能评估。在稳态条件下，电路中的电压和电流不随时间变化，网络中的能量存储元件如电容和电感不起作用。电阻网络的稳态分析通常关注于确定在恒定负载和输入条件下的电压、电流和功率分布。

在稳态分析中，可以使用欧姆定律和基尔霍夫定律对网络进行分析。稳态分析对于理解和设计电源供应、加热器、稳压器等应用至关重要。在实际应用中，稳态分析可以帮助工程师优化电路设计，确保在预期的负载条件下电路表现符合设计要求。

### 5.2.2 电阻网络的瞬态响应及其计算

瞬态分析涉及电路从一个稳态到另一个稳态的过渡期间的行为分析。在这一期间，电路中的电压和电流将随时间变化，能量存储元件将起主要作用。分析瞬态响应对于设计开关电路、脉冲发生器和其他时序敏感的电路非常重要。

瞬态分析的计算通常更为复杂，需要使用微分方程。在计算瞬态响应时，会使用初始条件和电路元件的特性（如电阻、电容和电感的阻抗特性）来求解电路方程。在瞬态分析中，可能需要借助于计算机模拟软件来获得精确的结果，因为手动计算通常只适用于简单的电路和简单的脉冲响应。

在实际应用中，瞬态分析可以帮助工程师预测电路在诸如电源开启、负载变化、脉冲信号输入等条件下的性能。这对于确保电路的稳定性和可靠性至关重要。

### 示例代码块

假设我们要模拟一个含有非线性电阻（例如热敏电阻）的简单电路的瞬态行为。我们可以使用SPICE软件（一种电路仿真工具）来进行模拟。以下是一个SPICE仿真文件的代码片段：

* 瞬态分析示例
.tran 1us 10ms
.include /path/to/resistor_model.cir

X1 1 2 RMODEL
RMODEL N+ N- R_THERM
R_THERM 1k 500 300
V1 1 0 DC 5V

.end

在这段代码中，`.tran` 命令用于指定仿真时间范围，`.include` 引入了热敏电阻的模型文件，`X1` 是电路中的非线性电阻元件，`RMODEL` 是实例化热敏电阻的标识，`R_THERM` 定义了热敏电阻的温度相关参数，`V1` 为电路提供直流电压。

请注意，本例中的代码是高度简化的，实际的模拟工作会更复杂，需要包含热敏电阻的详细模型参数，并可能需要更详细的电路结构和更长的仿真时间。通过运行仿真，我们可以得到电路中电压、电流随时间变化的波形图，从而分析电路的瞬态行为。

### 表格展示

为了更好地展示不同类型的电阻特性，下面的表格简要地总结了几种常见的非线性电阻的特性和应用：

| 非线性电阻类型 | 特性描述 | 典型应用 |
| -------------- | ------------ | ------------ |
| 热敏电阻 | 电阻随温度变化而变化 | 温度传感器，过电流保护 |
| 光敏电阻 | 电阻随光照强度变化而变化 | 光强度检测，自动调光系统 |
| 变阻器 | 可调节的电阻值 | 音量控制器，电流调节器 |

这个表格提供了对于非线性电阻类型和它们应用的快速了解，便于工程师在设计电路时根据需求选择适当的电阻类型。

### 流程图展示

下面是一个描述电阻网络中稳态与瞬态分析流程的mermaid流程图：

graph LR
    A[开始分析] --> B[确定电路类型]
    B --> C{是稳态分析吗?}
    C -- 是 --> D[应用欧姆定律和基尔霍夫定律]
    D --> E[计算稳态参数]
    C -- 否 --> F[应用微分方程]
    F --> G[进行瞬态模拟]
    G --> H[获取瞬态响应数据]
    E --> I[分析稳态结果]
    H --> I[分析瞬态结果]
    I --> J[优化电路设计]
    J --> K[结束分析]

这个流程图清晰地展示了电阻网络分析的决策流程，从稳态到瞬态分析的转变，以及最后如何基于分析结果优化电路设计。

## 5.2 非线性电阻与功率计算

### 5.2.1 非线性电阻特性的理解

非线性电阻是指那些其电阻值随电压或电流的变化而变化的电阻器。在电阻网络中，非线性电阻的出现使得计算变得更为复杂，因为它们不遵循欧姆定律 V=IR，其中电压与电流成线性关系。相反，非线性电阻的伏安特性曲线往往是弯曲的，表明电阻值随电压或电流的变化而变化。

理解非线性电阻的特性对于在复杂电路中进行准确的计算至关重要。一些常见的非线性电阻包括：

- **热敏电阻 (Thermistors)**: 其电阻值随温度显著变化，用于温度传感器。
- **光敏电阻 (Photoresistors)**: 其电阻值随光照强度变化，用于光强度控制。
- **变阻器 (Varistors)**: 它们能够承受高电压，并在一定电压范围内改变它们的电阻值，用于过压保护。

### 5.2.2 功率在电阻网络中的计算方法

功率计算在任何电气网络中都是一个核心概念。在非线性电阻网络中，功率 P 的计算公式依然为 P = V × I，但是由于非线性电阻的伏安关系并非线性，所以不能简单地将电压 V 和电流 I 直接相乘来计算功率。功率的计算往往需要依赖于电阻随电压或电流变化的具体关系。

举个例子，如果一个非线性电阻的伏安特性是已知的，即电阻值 R 对应的电压 V 已知，那么可以使用积分的方法来计算功率消耗。公式可以表达为：

\[ P = \int_{0}^{V} \frac{V}{R(V)} dV \]

其中 R(V) 是电压 V 下电阻的阻值。这种积分运算通常需要借助数学软件或数值计算方法来完成。理解这种计算的原理对于解决实际电路问题至关重要，尤其是在设计电源和控制电路时。

### 代码块与参数说明

在实际应用中，工程师常常需要对含有非线性电阻的电路进行仿真以分析其性能。例如，使用MATLAB或者Python中的SciPy库可以方便地进行数值积分计算。下面是一个使用Python进行非线性电阻功率计算的示例代码：

import scipy.integrate as spi

# 假设我们知道非线性电阻的伏安特性函数
def v_from_i(V):
    # 这里是根据非线性电阻特性定制的函数
    # 例如，使用多项式逼近真实的伏安特性曲线
    # 在实际情况下，可能需要从数据中拟合此函数
    return a*V**3 + b*V**2 + c*V + d

# 计算功率的函数
def calculate_power(V_min, V_max):
    # 通过数值积分计算功率
    power, _ = spi.quad(lambda V: V / v_from_i(V), V_min, V_max)
    return power

# 假定非线性电阻在电压 V_min 和 V_max 下工作
V_min = 1
V_max = 10

# 计算功率
power = calculate_power(V_min, V_max)
print(f"计算得到的功率为: {power} watts")

在这个代码示例中，我们假设了一个非线性电阻的伏安特性函数 `v_from_i`，然后通过 `calculate_power` 函数使用数值积分方法来计算在一定电压范围内的功率消耗。这为工程师提供了一种在不依赖于简化模型的情况下，精确计算复杂电路中功率的方法。

在进行这种计算时，选择合适的积分区间（`V_min` 和 `V_max`）是非常关键的，它需要基于实际电路的工作范围来决定。注意，参数 `a`、`b`、`c`、`d` 是根据实际电路特性确定的，这里只是作为示例。

### 逻辑分析

本节我们主要讨论了非线性电阻网络中功率计算的高级技巧。由于非线性电阻的特性，不能简单地使用欧姆定律来计算功率，而需要采用更复杂的数值方法，例如积分计算。在实际应用中，工程师必须对电路中的非线性元件有深入的理解，以确保电路设计能够满足性能要求。

理解非线性电阻的特性，并能够精确计算其在电路中的功率消耗，对于确保电路的高效能和可靠性至关重要。特别是对于电源电路、温度控制电路等，在这些应用中，非线性电阻的性能直接影响整个系统的稳定性和响应速度。

通过实际的代码实现，我们能够看到如何在电路仿真和分析中应用这些高级技巧。此类仿真工具和数值方法能够帮助工程师设计更稳健、更精确的电路，并在电路设计初期阶段识别潜在的问题。此外，对于现有电路的故障诊断和优化，这些高级技巧同样具有极大的价值。

在下一节中，我们将探讨电阻网络中的稳态与瞬态分析，进一步深化我们对于电路行为的理解，特别是在电路响应变化时如何分析和预测其性能。

# 6. 电阻网络的实际应用案例

电阻网络作为电子电路的基础构建模块，广泛应用于电子设计与故障诊断中。本章节将通过具体案例探讨电阻网络在实际中的应用和故障处理。

## 6.1 电路设计中的电阻网络应用

在电路设计阶段，电阻网络可作为信号分压器、滤波器、电流限制器等多种功能的角色。

### 6.1.1 设计简单的电阻网络电路

设计一个简单的电阻网络电路通常涉及选择合适的电阻值以满足特定的电压或电流分配需求。例如，设计一个分压器来为一个运算放大器提供参考电压。

graph TD
    A[输入电压] -->|V_in| B[电阻R1]
    B --> C[电阻R2]
    C -->|V_out| D[输出电压]
    B -->|V_drop| E[地]

这里，R1和R2的值根据所需的V_out来确定：

V_out = V_in * (R2 / (R1 + R2))

### 6.1.2 电阻网络在电子设备中的实际应用

在许多电子设备中，如电源适配器、信号调节电路和数字逻辑电路，电阻网络作为电路的组成部分，用于提供精确的电压和电流控制。例如，LED驱动电路中使用电阻网络来限制电流，防止LED过热损坏。

## 6.2 电阻网络故障诊断与修复

电阻网络故障可能由多种原因引起，包括元件老化、过载、短路等。

### 6.2.1 常见的电阻网络故障类型

以下是一些常见的电阻网络故障类型及其可能的原因：

- 开路故障：由于物理损伤、焊接不良或过载导致的导线断裂。
- 短路故障：由于导电异物、潮湿或元件损坏导致电路中出现非预期的导电路径。
- 参数漂移故障：由于长时间使用或环境变化导致电阻值的改变。

### 6.2.2 故障诊断与修复的策略与方法

故障诊断过程应该系统且有序。例如，在诊断一个疑似短路的电阻网络时，可以使用多用电表测量电阻值，与设计规格进行对比。如果电阻值远低于预期，可能存在短路。

flowchart LR
    A[开始检测] --> B[使用多用电表检测电阻值]
    B --> C[电阻值是否正常?]
    C -->|是| D[无故障]
    C -->|否| E[检查电路板]
    E --> F[是否发现短路迹象?]
    F -->|是| G[修复短路]
    F -->|否| H[更换损坏电阻]
    G --> I[重新检测]
    H --> I[重新检测]
    I --> J{重新检测是否通过?}
    J -->|是| D
    J -->|否| B

修复策略包括替换损坏的电阻、重新焊接接点、清洗或替换潮湿损坏的电路板等。在修复完成后，应重新进行测试以确保故障已被彻底修复。

通过这些具体的案例，我们可以更深入地理解电阻网络的实际应用，以及在实际工作中遇到故障时如何进行诊断与修复。在下一章节中，我们将探讨电阻网络的高级计算技巧，包括处理非线性电阻和瞬态分析等内容。