【向量推动现代计算】：向量知识在三维建模和游戏开发中的革命性应用


# 摘要
向量计算是计算机图形学、游戏开发、物理模拟和许多其他领域的核心组成部分。本文深入探讨了向量在三维建模、游戏开发以及进阶技术主题中的理论基础和应用实践。通过对向量在几何构建、图形渲染、模型简化、游戏物理、AI行为建模和界面设计中的角色进行分析，本文展示了向量技术如何提高性能和精确性。进一步地，探讨了向量编程、GPU加速、虚拟现实、增强现实技术与向量技术的结合，并分析了向量技术未来的发展趋势，如向量在计算机视觉和深度学习中的应用。最后，通过案例分析，本文提供了向量应用的策略和教训，揭示了向量技术在实际场景中的有效性和创新点。

# 关键字
向量计算；三维建模；游戏开发；并行计算；虚拟现实；深度学习

参考资源链接：[高中数学知识笔记大全.pdf](https://wenku.csdn.net/doc/6401ad08cce7214c316ee0b1?spm=1055.2635.3001.10343)
# 1. 向量计算的理论基础

## 1.1 向量概念及其重要性
向量是数学中一种基础而强大的工具，其不仅能表示具有大小和方向的量，还涉及到多个科学与工程领域的核心计算。在计算机图形学、物理模拟、数据分析等众多领域，向量计算都是不可或缺的基础，为复杂的多维问题提供了简洁而高效的解决途径。

## 1.2 向量的基本运算
向量计算包括向量的加减乘除，以及标量与向量之间的运算。例如，两个向量相加或相减是通过对应分量的运算得到新向量；向量与标量相乘则是每个分量乘以该标量。这些基本操作是进行更复杂数学运算的基础。

## 1.3 向量在几何空间中的应用
向量的运算可以推广到几何空间中的点、线、面的表示和变换。例如，使用向量可以方便地表达平面方程，进行线性变换以及在三维空间中描述物体的位置和方向。这一理论基础是后续章节中三维建模和游戏开发中向量技巧应用的基石。

# 2. 三维建模中的向量应用

### 2.1 向量在几何构建中的作用

#### 2.1.1 点、线、面的向量表示

在三维空间中，点、线、面是构成几何形体的基础元素。通过向量表示这些元素，可以更精确地进行计算和分析。每一个几何体的位置、方向和形状都可以通过向量坐标和向量运算来表达。

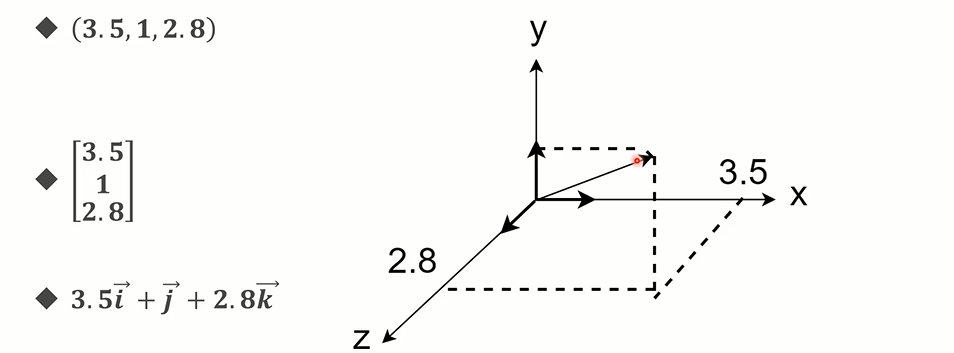
点在三维空间中可以表示为一个三元组 (x, y, z)，其中x, y, z分别表示该点在三个坐标轴上的位置。线可以通过两个点来定义，这两个点可以构成一个向量，表示线的方向和长度。而面通常由三个不共线的点定义，这三个点构成的向量可以确定面的法向量，从而确定面的方向。

例如，给定两个点 P1(x1, y1, z1) 和 P2(x2, y2, z2)，连接这两点的线可以表示为向量 P1P2 = [x2 - x1, y2 - y1, z2 - z1]。面可以由点 P1、P2 和 P3 构成，三个向量 P1P2、P2P3 和 P3P1 可以确定面的方向。

#### 2.1.2 向量运算在几何变换中的应用

几何变换是三维建模中的一个核心概念，主要包括平移、旋转和缩放。向量运算在这些变换中起到了关键作用。通过向量加法可以实现平移，而旋转可以通过矩阵乘法与向量的组合来实现。

- **平移**：平移变换可以简单地通过向量加法实现。假设存在一个点 P 和向量 V，平移后的新点 P' 可以通过 P' = P + V 来计算。

  # Python 示例代码，表示向量平移
  P = [x, y, z]  # 原始点坐标
  V = [dx, dy, dz]  # 平移向量
  P_prime = [P[i] + V[i] for i in range(3)]  # 平移后的点坐标

- **旋转**：在三维空间中，旋转通常需要使用旋转矩阵，该矩阵可以与向量相乘以实现旋转效果。例如，绕 Z 轴旋转一个角度 theta 可以用下面的旋转矩阵 Rz(θ) 与向量相乘。

  import numpy as np
  theta = np.radians(45)  # 旋转角度转换为弧度
  Rz = np.array([
      [np.cos(theta), -np.sin(theta), 0],
      [np.sin(theta), np.cos(theta), 0],
      [0, 0, 1]
  ])
  V = np.array([x, y, z])  # 向量坐标
  V_rotated = np.dot(Rz, V)

平移和旋转是三维图形编程中最常见的变换，它们通过向量运算变得简单而直观。在渲染管线中，这些变换可以用来对模型进行动态的位置和方向调整。

### 2.2 向量与三维图形渲染技术

#### 2.2.1 光线追踪与向量计算

光线追踪是一种通过追踪虚拟光线在三维场景中的传播来生成图像的技术。光线与物体表面的交互，如反射、折射和阴影，都需要复杂的向量计算来实现。每一个光线都可以表示为从相机出发的向量，物体表面与光线的交点可以表示为另一个向量。光线追踪算法通过向量运算来计算光线路径、交点和相关属性。

graph LR
A[开始光线追踪] --> B[定义视点向量]
B --> C[从视点向量发射光线]
C --> D[计算光线与物体交点]
D --> E[确定交点处的光照]
E --> F[渲染最终图像]

光线与物体的交点通过解光线方程和物体表面方程得到。例如，若物体为平面，其表面方程为 Ax + By + Cz + D = 0，那么交点可以通过求解光线方程和平面方程来得到。对于复杂曲面，通常需要数值方法来求解交点。

#### 2.2.2 纹理映射与向量插值

纹理映射是将二维纹理图片应用到三维模型表面的过程，它是增加模型视觉效果的重要技术。在纹理映射中，模型表面的每一个点需要根据其在纹理上的对应点来计算纹理坐标。这一过程通常需要利用向量插值技术来实现。

向量插值可以在两个已知的向量间生成一个连续变化的向量序列。在纹理映射中，利用插值技术可以计算出物体表面上任一点的纹理坐标。例如，线性插值（lerping）用于在两个顶点间进行插值，而双线性插值（bilinear interpolation）用于在纹理的四个顶点间进行插值。

def lerp(v1, v2, t):
    """
    线性插值函数
    :param v1: 向量1
    :param v2: 向量2
    :param t: 插值参数[0, 1]
    :return: 插值结果
    """
    return v1 + t * (v2 - v1)

纹理映射与向量插值是提高渲染质量和效果的重要手段，它们通过向量计算来实现高度真实感的视觉效果。

### 2.3 向量优化算法在模型简化中的应用

#### 2.3.1 几何简化与顶点聚类

在三维建模和渲染中，为了减少计算量和提高渲染速度，常常需要对模型进行简化。几何简化技术能够减少模型中不必要的细节，而顶点聚类是一种有效的简化方法。在顶点聚类过程中，使用向量距离和向量运算来判断哪些顶点可以合并或者删除。

顶点聚类算法中一个关键步骤是基于向量距离的合并条件判断。通过计算两个顶点向量间的欧几里得距离，可以确定它们是否足够接近而可以被视为同一顶点。聚类算法会将距离小于特定阈值的顶点合并，从而减少模型的复杂度。

def distance(v1, v2):
    """
    计算两个三维向量间的欧几里得距离
    :param v1: 向量1
    :param v2: 向量2
    :return: 距离值
    """
    return np.linalg.norm(np.array(v1) - np.array(v2))

在进行顶点聚类时，通常还需要考虑顶点的法向量，以确保简化操作不会对模型的表面特性产生不良影响。通过向量运算来优化模型，可以在保持模型外观的前提下显著减少模型的复杂性。

#### 2.3.2 实时渲染的优化策略

实时渲染是游戏和虚拟现实应用中不可或缺的技术。为了在有限的硬件资源下达到流畅的渲染效果，实时渲染系统会采用多种优化策略，包括剔除（Culling）、层级细节（LOD）技术和遮挡剔除（Occlusion Culling）。

剔除是实时渲染中的一种常见优化技术，其目的是减少不必要的渲染计算。通过向量运算来判断物体是否在摄像机视野内，或者物体间是否有遮挡关系。例如，视锥剔除（Frustum Culling）通过计算物体与视锥体的位置关系来确定是否渲染该物体。

层级细节（LOD）技术则是根据物体与摄像机的距离来动态调整物体的细节程度。距离摄像机近的物体使用高细节模型，距离远的物体使用低细节模型，这可以显著减少渲染的计算量。在LOD技术中，向量运算用于计算物体位置与摄像机距离，以决定物体的细节级别。

def calculate_distance_to_camera(vertices, camera_position):
    """
    计算顶点到摄像机的距离
    :param vertices: 顶点坐标列表
    :param camera_position: 摄像机位置
    :return: 顶点到摄像机的距离列表
    """
    return [np.linalg.norm(np.array(vertex) - np.array(camera_position)) for vertex in vertices]

实时渲染的优化是一个复杂的问题，涉及到多种技术的综合应用。通过向量运算来优化渲染性能是提升用户体验的关键因素之一。

# 3. 游戏开发中的向量技巧

## 3.1 向量在游戏物理中的应用
### 3.1.1 动力学模拟与向量分析
在游戏开发中，物理模拟是创造真实体验的关键元素之一。通过向量的使用，开发者可以模拟物体在空间中的运动，包括速度、加速度、力的施加等。向量分析在动力学模拟中非常关键，因为它可以帮助开发者以数学的方式描述和计算物体的运动特性。

向量在动力学中的应用例子之一是牛顿运动定律的实现。在游戏中模拟一个物体的运动，需要考虑质量、施加的力和产生的加速度，其关系可以表示为 `F = m*a`，其中 `F` 是力向量，`m` 是物体的质量，`a` 是加速度向量。通过这个简单的公式，我们能够计算物体在受到不同力时的运动状态。

要实现这一功能，游戏物理引擎通常会包含向量数学库，该库会提供一系列的向量操作函数，比如向量加法、减法、点乘、叉乘等，以支持复杂的物理模拟。

#### 示例代码块
假设我们要模拟一个飞船在二维空间中的受力运动，可以通过以下代码片段来进行基本的向量计算：

#include <iostream>
#include <cmath> // 引入数学库，用于计算向量角度

struct Vector2D {
    double x, y;
    // 向量加法
    Vector2D operator+(const Vector2D& other) const {
        return {x + other.x, y + other