【时间序列数据处理】：动态数据处理的10大技巧


# 摘要
本文系统地探讨了时间序列数据处理和预测的全面知识体系。首先介绍了时间序列数据处理的基础概念和重要性，接着深入讨论了数据预处理技巧，包括数据清洗、标准化与转换以及频率转换。第三章聚焦于特征提取方法，包括统计特征分析、信号处理方法和模型驱动的特征。在第四章中，我们构建了多种时间序列预测模型，从传统方法到机器学习和深度学习技术。第五章展示了时间序列数据在不同领域的实战应用。最后，第六章展望了时间序列分析的高级技巧、软件工具以及未来的发展趋势，强调了集成方法和不确定性量化的重要性。本文为研究者和实践者提供了时间序列分析的完整指南，旨在提高数据处理的效率和预测的准确性。

# 关键字
时间序列数据；数据预处理；特征提取；预测模型；实战应用；不确定性量化

参考资源链接：[马利科夫判据与阿卑-赫梅特法：系统误差的精确识别](https://wenku.csdn.net/doc/6rnrxsx3hq?spm=1055.2635.3001.10343)
# 1. 时间序列数据处理概念

在进行时间序列分析之前，了解其核心概念至关重要。时间序列数据是一系列按照时间顺序排列的观测值，它反映了某一变量随时间变化的趋势、周期性和随机性。这些数据可以是一秒一次的高频数据，也可以是年度数据，它们广泛应用于经济学、金融学、环境科学等领域。

时间序列分析的目的是为了从历史数据中提取有用信息、预测未来走势或者识别数据中蕴含的模式。这通常包括数据的预处理、特征提取、模型构建以及模型验证等步骤。在这一过程中，处理者需要熟悉各种统计和机器学习技术，并能合理选择和使用相应的工具和方法。

在本章中，我们将介绍时间序列数据的基本概念，以及如何将数据组织成可分析的格式。这包括理解时间序列数据的基本属性，如平稳性、季节性和趋势，以及如何检查数据的一致性和完整性。此外，我们还将探讨时间序列数据的种类和应用场景，为后续深入分析打下坚实的基础。

# 2. 时间序列数据的预处理技巧

在分析和预测时间序列数据之前，必须进行彻底的数据预处理。预处理的目标是清理数据，使其更适合于建模过程。本章将详细介绍时间序列数据清洗、标准化和转换的技巧。

### 2.1 数据清洗

数据清洗是时间序列分析中不可或缺的步骤，它包括处理缺失值和检测及修正异常值。

#### 2.1.1 缺失值处理方法

缺失值是在数据集中未记录的值，可能是由于各种原因，如数据采集故障或记录损坏。处理缺失值的方法有多种：

- **删除含有缺失值的记录**：如果缺失值很少，直接删除这些记录通常不会造成太大问题。不过，这样做可能会导致丢失有用的信息，特别是当数据集较小时。
- **填充缺失值**：可以使用之前观测值的平均数、中位数、众数，或者基于模型的预测来填补缺失值。这种方法特别适用于时间序列数据，因为它可以保持数据的顺序性。例如，使用前一个观测值填充，称为“前向填充”，使用后一个观测值填充，称为“后向填充”。
下面是一个使用Python填充缺失值的示例代码：

  import pandas as pd
  import numpy as np

  # 创建一个带有缺失值的时间序列DataFrame
  data = pd.Series([10, 12, np.nan, 14, 15, np.nan, 17])

  # 使用前向填充方法填充缺失值
  data_filled_forward = data.fillna(method='ffill')

  # 使用后向填充方法填充缺失值
  data_filled_backward = data.fillna(method='bfill')

  print(data_filled_forward)
  print(data_filled_backward)

在这个例子中，`fillna`函数与`method`参数用于指定填充方法。`ffill`代表前向填充，`bfill`代表后向填充。代码逻辑中，我们首先创建了一个包含NaN（代表缺失值）的时间序列数据，然后分别展示了如何应用前向和后向填充技术。

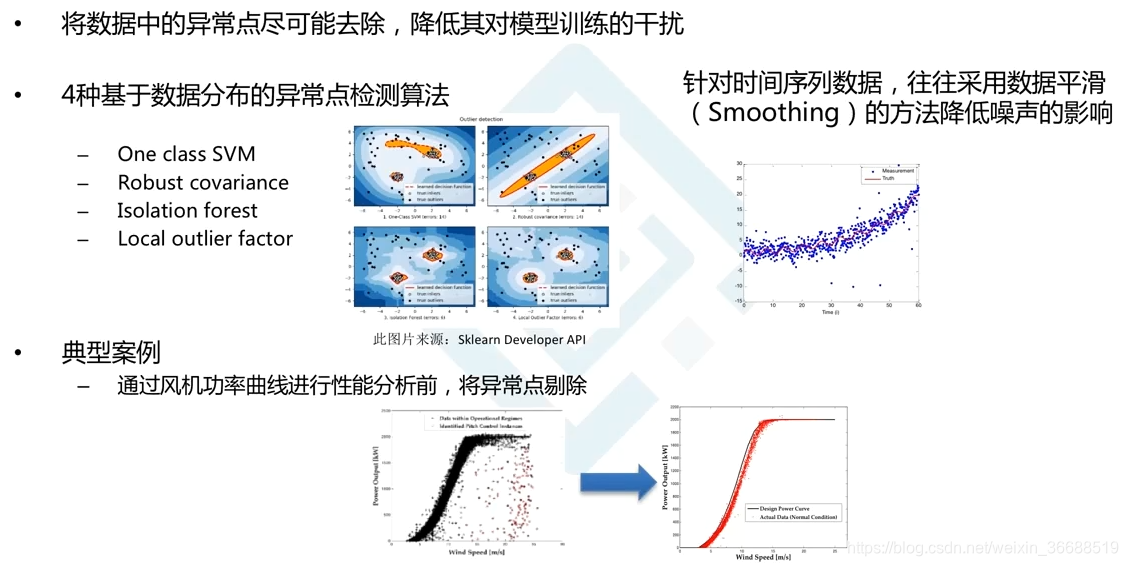
#### 2.1.2 异常值检测与修正

异常值是明显偏离数据集其他观测值的值。异常值可能是错误，也可能是数据中的真实变异，但它们可能会对分析结果产生重大影响。

- **异常值检测**：检测异常值常用的方法包括标准差方法（比如，认为超过均值加减3倍标准差的值为异常），箱线图（位于IQR之外的值通常被认为是异常值），以及基于模型的方法。
- **异常值修正**：一旦检测到异常值，就需要决定如何处理它们。简单的处理方式是用缺失值处理方法替换异常值，或者使用基于模型的方法进行调整。

### 2.2 数据标准化与转换

数据标准化和转换是将数据转换成更适合进行分析和建模的过程。

#### 2.2.1 数据归一化技术

数据归一化是将数据按比例缩放，使之落入一个小的特定区间。常见的数据归一化技术是将数据缩放到[0,1]区间内，也称为最小-最大归一化。

  from sklearn.preprocessing import MinMaxScaler
  import numpy as np

  # 生成一组数据
  data = np.array([100, 200, 300, 400, 500])

  # 初始化归一化器
  scaler = MinMaxScaler()
  # 对数据进行归一化处理
  normalized_data = scaler.fit_transform(data.reshape(-1,1))
  print(normalized_data)

在这个例子中，我们使用了`MinMaxScaler`函数，将数据缩放到[0,1]区间内。`fit_transform`方法先拟合数据，然后进行转换。最终输出归一化后的数据。

#### 2.2.2 数据转换的数学方法

数据转换包括对原始数据进行数学操作，比如对数转换、平方根转换、倒数转换等，目的是将数据转换为更适合分析的形式，如使数据更接近正态分布。

### 2.3 时间序列的频率转换

时间序列的频率转换是指改变数据的时间序列频率，例如从日数据转换为月数据。

#### 2.3.1 重采样与插值技术

重采样是改变数据频率的过程。对于时间序列数据，这通常意味着将数据从一个频率转换到另一个频率。插值技术用于在重采样过程中填充新创建的时间点。

import pandas as pd
import numpy as np

# 创建一个日期范围和一个随机数据
data = pd.Series(np.random.randn(100), index=pd.date_range('20200101', periods=100))

# 将日数据转换为月数据
monthly_data = data.resample('M').mean()

# 重采样后插入缺失值
monthly_data_filled = monthly_data.interpolate(method='linear')

print(monthly_data)
print(monthly_data_filled)

在这个例子中，我们首先创建了一个日数据集，然后使用`resample`方法将其转换为月数据。默认情况下，`resample`会对数据进行平均值计算，以得到新的频率数据。接着，使用`interpolate`方法对重采样后的数据进行插值，这里采用了线性插值法。

#### 2.3.2 分解与重构时间序列

时间序列分解是将时间序列分解为趋势、季节性和周期性成分的过程。重构则是将这些分解后的部分重新组合成原始时间序列的过程。

下面是一个分解和重构时间序列数据的示例：

from statsmodels.tsa.seasonal import seasonal_decompose

# 创建一个正弦波数据，模拟季节性时间序列
data = pd.Series(np.sin(np.arange(0, 10, 0.1)*2*np.pi) + np.random.normal(0, 0.5, 100))

# 分解时间序列
decomposition = seasonal_decompose(data, model='additive')

# 分解出的趋势、季节性和残差
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid

# 重构时间序列
reconstructed = trend + seasonal + residual

print(reconstructed.head())

在这个例子中，我们使用`seasonal_decompose`函数，通过加法模型分解出趋势、季节性和残差。然后，我们简单地将这些成分相加，以重构原始的时间序列。这种方法可用于识别和理解数据中的不同成分，从而对时间序列进行更好地分析和预测。

# 3. 时间序列数据的特征提取

## 3.1 统计特征分析

### 3.1.1 常用统计量的计算方法

时间序列数据的统计特征分析是从数据中提取有用信息的重要步骤。常用统计量包括均值（mean）、中位数（median）、标准差（standard deviation）、偏度（skewness）和峰度（kurtosis）。这些统计量可以帮助我们从不同角度理解数据的分布特征。

均值提供了数据集的中心位置，而标准差衡量了数据的离散程度。偏度描述了分布的不对称性，正偏度表示数据的尾部向右延伸，负偏度则相反。峰度则是衡量数据分布尖峭或平坦的程度，高峰度表示数据集中出现了更多的极端值。

在Python中，可以使用`numpy`库来快速计算这些统计量。例如，计算一个时间序列数据集的均值、标准差和偏度的代码如下：

import numpy as np

# 假设 time_series 是一个时间序列数据集
time_series = np.array([12, 15, 13, 17, 18, 14, 19])

# 计算均值、标准差和偏度
mean_value = np.mean(time_series)
std_dev = np.std(time_series)
skewness = np.skew(time_series)

print(f"均值: {mean_value}")
print(f"标准差: {std_dev}")
print(f"偏度: {skewness}")

在实际应用中，可以使用类似的方法来探索数据集，找出数据集的潜在特征和规律。

### 3.1.2 趋势、季节性和周期性分析

时间序列的分解通常关注于识别数据中的趋势（trend）、季节性（seasonality）和周期性（cyclicity）成分。

趋势代表了数据随时间的长期变动方向，例如，随着时间的推移，销售额可能呈现上升或下降的趋势。季节性指的是周期性重复出现的模式，例如，每个星期的销售模式可能在工作日与周末之间有所不同。周期性则是指非固定频率的波动，往往与经济周期或其他长周期事件相关。

分析这些成分通常需要采用特定的统计方法，如移动平均线（Moving Average）和季节性分解时间序列（Seasonal Decomposition of Time Series, STL）。例如，使用Python中的`statsmodels`库进行时间序列的季节性分解：

import statsmodels.api as sm

# 假设 monthly_data 是按月记录的数据集
monthly_data = np.array([13, 15, 13, 17, 18, 14, 19, 16, 14, 15, 17, 18])

# 使用 STL 进行季节性分解
decomposition = sm.tsa.seasonal_decompose(monthly_data, model='additive', period=12)
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid

# 输出分解结果
print(f"趋势成分: {trend}")
print(f"季节性成分: {seasonal}")
print(f"残差: {residual}")

通过这种分解，我们能够更好地理解时间序列数据的行为，并为后续的预测和分析工作奠定基础。

## 3.2 信号处理方法

### 3.2.1 离散傅里叶变换（DFT）应用

离散傅里叶变换（Discrete Fourier Transform, DFT）是一种将时域信号转换为频域表示的方