【降噪系统架构全解】:LMS算法在多麦克风配置中的核心地位


基于LMS算法的多麦克风降噪系统.rar
摘要
本文综述了LMS算法在降噪系统中的应用,并探讨了其理论基础、系统架构以及优化策略。文中首先介绍了自适应滤波器和LMS算法的原理,阐述了其工作机制及数学模型,并讨论了标准LMS算法的变种与性能优化。接着,文章聚焦于多麦克风降噪技术,深入分析了其声学原理、LMS算法在多麦克风系统中的具体应用,以及实际案例分析。第四章详细描述了降噪系统的设计与实现,包括硬件和软件设计、LMS算法的实现技术以及系统集成与测试。最后,文章展望了LMS算法在通信、生物医学工程等其他领域的应用前景,并对算法的未来发展趋势和改进方向进行了预测。本文为理解LMS算法的原理、应用及优化提供了全面的参考,对促进降噪技术的发展具有重要意义。
关键字
LMS算法;自适应滤波器;降噪系统;多麦克风技术;系统集成;实时性优化
参考资源链接:基于LMS算法的多麦克风语音降噪实现
1. 降噪系统架构概述
在探讨降噪系统的工作原理之前,了解其架构是非常重要的。降噪系统架构是一个多层次、多组件的结构,它通常包括信号采集、预处理、滤波处理和后处理等多个部分。架构的核心在于将噪声抑制到最小,同时尽量保持或提高信号的原始质量。
1.1 系统架构组件
降噪系统架构由以下基本组件构成:
- 信号采集模块:通常使用麦克风或其他传感器来接收声音信号。
- 预处理模块:处理初始信号,包括放大、滤波和转换信号格式等。
- 滤波处理模块:这是降噪系统的核心,使用不同的算法例如LMS(最小均方)算法对噪声进行消除。
- 后处理模块:优化经过滤波处理的信号,例如进行降噪后的质量评估。
1.2 系统工作流程
从信号采集到输出,降噪系统的工作流程是连贯的:
- 信号采集:首先,从环境或设备中采集到含有噪声的原始信号。
- 预处理:进行必要的信号增强和特征提取,准备滤波处理。
- 滤波处理:运用LMS算法或其它降噪算法从信号中去除或减少噪声。
- 后处理:最终处理和优化滤波后的信号,准备输出或存储。
通过这种多层次的处理流程,降噪系统能有效减少不需要的背景噪声,而保留有用信号的清晰度。在后续章节中,我们将深入探讨LMS算法及其在降噪系统中的应用,以及如何优化整个降噪过程。
2. LMS算法理论基础
2.1 自适应滤波器原理
2.1.1 自适应滤波器的定义与功能
自适应滤波器是一种动态系统,它可以根据输入信号的特性自动调整自身的参数,以达到优化某一性能指标的目的。在降噪系统中,自适应滤波器的主要功能是通过不断的调整其内部参数来最小化误差信号,即实际接收到的声音信号与期望信号之间的差异。
自适应滤波器通常由以下几部分组成:
- 输入信号:即系统需要处理的原始信号,例如环境噪声和语音信号的混合。
- 参考信号:通常是一个或多个辅助输入,可以是噪声信号或其他已知信号,用以协助滤波器进行学习和调整。
- 误差信号:输入信号与经过滤波器处理后的信号之差。
- 滤波器系数(权重):自适应滤波器的关键参数,通过调整这些系数可以控制滤波器的性能。
- 更新算法:负责根据误差信号调整滤波器系数以达到学习目的的算法,例如最小均方(LMS)算法。
2.1.2 自适应滤波器的数学模型
自适应滤波器的数学模型可以用来描述其工作原理。一个简单的自适应滤波器模型通常可以表示为:
- ( x(n) ):在时间步 ( n ) 的输入信号。
- ( d(n) ):在时间步 ( n ) 的参考信号。
- ( y(n) ):在时间步 ( n ) 的输出信号,是输入信号与滤波器系数的加权和。
- ( e(n) ):在时间步 ( n ) 的误差信号,表示为 ( e(n) = d(n) - y(n) )。
- ( w(n) ):在时间步 ( n ) 的滤波器系数向量。
滤波器的输出 ( y(n) ) 可以通过以下公式计算:
[ y(n) = \sum_{i=0}^{M-1} w_i(n) x(n-i) ]
其中,( M ) 是滤波器的阶数,( w_i(n) ) 是时间步 ( n ) 的第 ( i ) 个系数。
误差信号 ( e(n) ) 用于驱动更新过程,它反馈到滤波器中以更新系数 ( w_i(n) ),使 ( e(n) ) 最小化。
2.2 LMS算法原理详解
2.2.1 LMS算法的工作机制
最小均方(LMS)算法是最简单的自适应滤波算法之一。它的工作机制主要基于最速下降法,通过最小化误差信号的均方值来调整滤波器系数。LMS算法的核心思想是利用当前误差信息来估计梯度,并用这个估计来更新滤波器系数。
LMS算法的基本步骤如下:
- 初始化滤波器系数 ( w(0) )。
- 对于每一个时间步 ( n = 0, 1, 2, … ),计算输出信号 ( y(n) )。
- 计算误差信号 ( e(n) = d(n) - y(n) )。
- 利用误差信号更新滤波器系数 ( w(n+1) = w(n) + \mu e(n) x(n) ),其中 ( \mu ) 是步长参数。
- 重复步骤2至4直至系数收敛或达到某个停止准则。
2.2.2 LMS算法的数学表达和稳定性分析
从数学角度讲,LMS算法的目标是最小化下面的均方误差(MSE)函数:
[ J(w) = E\left[|e(n)|^2\right] = E\left[|d(n) - y(n)|^2\right] ]
其中 ( E ) 表示期望值。在LMS算法中,我们通过迭代的方式来近似这个过程。系数更新公式可以看作是MSE函数在 ( w(n) ) 处的负梯度方向上的一个步骤。
关于LMS算法的稳定性,其稳定性取决于步长参数 ( \mu )。如果步长太大,滤波器可能会变得不稳定,即系数会在最优解附近震荡而不是收敛。相反,如果步长太小,滤波器的收敛速度会非常慢。步长参数的选择对LMS算法的性能至关重要。
2.3 LMS算法的变种与优化
2.3.1 标准LMS与变种算法对比
标准LMS算法是自适应滤波中最基本的算法,但随着研究的深入,许多变种算法被提出来解决特定问题。例如:
- 归一化LMS (NLMS):自动调整步长 ( \mu ),使其与输入信号的功率成比例,改善了收敛速度与稳定性。
- 变换域LMS: 在频域中进行自适应滤波,可以更快地处理高阶滤波器。
- 子带LMS: 将信号分解到多个子带进行处理,能够有效减少计算量。
每种变种算法都有其优缺点,并且它们的设计目标也各有不同,有的是为了提高收敛速度,有的是为了减少计算复杂度。
2.3.2 LMS算法的性能优化策略
为了进一步提高LMS算法的性能,可以采取以下策略:
- 初始化策略: 使用合适的方法初始化滤波器系数可以加快收敛速度,例如使用小的随机值或基于信号统计特性进行初始化。
- 步长调整: 可以动态调整步长 ( \mu ) 以在收敛速度和稳定性之间进行权衡。
- 正则化技术: 在更新规则中加入正则化项可以防止过拟合,尤其是在数据量有限的情况下。
- 并行处理: 利用多核处理器或专用硬件加速LMS算法的计算,可以显著提高处理速度。
通过这些优化策略,可以针对不同的应用场景和性能要求定制LMS算法的实现,从而达到更好的降噪效果。
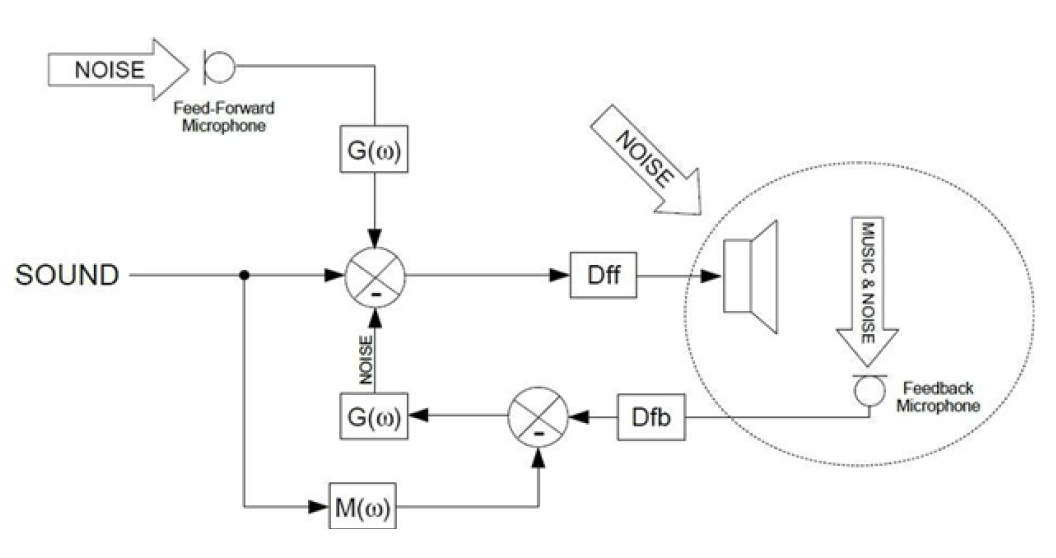
3. 多麦克风降噪技术
3.1 多麦克风配置的声学原理
3.1.1 声波的传播与麦克风阵列效应
在解释声波在空间中的传播和多麦克风阵列效应之前,我们首先需要理解声波的基本特性。声波是一种机械波,它通过介质传播时,介质的分子会发生振动,并以波动的形式传递能量。在自由场环境下,声波会以球面波的形式向外扩散,其能量随着距离的增加而衰减。
麦克风阵列通过空间上分布的多个麦克风捕捉声音信号,利用各麦克风接收到的声波之间的时差和强度差,实现对声源的定位、跟踪以及声场的分析。阵列效应的关键在于利用这些差分信息来区分直达声和反射声,从而抑制环境噪声并提高目标信号的清晰度。
为了更好地理解麦克风阵列效应,我们使用一个简单的两麦克风系统来说明。当两个麦克风被放置在一定距离上时,它们会分别接收到来自声源的直达波,以及由周围环境反射的反射波。通过比较两个麦克风接

































