【最新趋势】：MATLAB与艾伦方差结合的MEMS陀螺仪噪声分析方法

# 1. MEMS陀螺仪技术概述

## 1.1 MEMS陀螺仪的工作原理
MEMS陀螺仪是一种利用微电子机械系统(Micro-Electro-Mechanical Systems, MEMS)技术制造的微型陀螺仪。其基本原理基于科里奥利力。当一个振动质量在运动时，如果设备受到角速度的影响，那么质量将会受到一个垂直于其速度和旋转轴的科里奥利力的作用。这个力会导致振动质量相对于支撑结构产生位移，通过检测这个位移，就能测得角速度。

## 1.2 MEMS陀螺仪的关键技术指标
MEMS陀螺仪的关键技术指标包括测量范围、灵敏度、分辨率、零点偏移、温度敏感性等。测量范围决定了陀螺仪能够测量的最大角速度；灵敏度则是指对角速度变化的敏感程度；分辨率是区分两个连续不同角速度的能力；零点偏移指的是在无输入的情况下测量值与理论零值的偏差；温度敏感性涉及陀螺仪输出随温度变化的程度。

## 1.3 MEMS陀螺仪的应用领域
由于其体积小、功耗低、成本低廉以及易于批量制造等特点，MEMS陀螺仪被广泛应用于消费电子、汽车、航空航天、机器人等领域。例如，用于手机的姿势控制、车辆的稳定系统、飞机的飞行控制以及机器人的平衡与导航等。随着技术的进步，MEMS陀螺仪在精度和可靠性上不断取得突破，其应用范围也在持续扩大。

# 2. 艾伦方差理论基础

## 2.1 艾伦方差的定义和数学模型

### 2.1.1 艾伦方差的数学公式解释

艾伦方差（Allan Variance），通常表示为σy(τ)，是一种用于评估时间频率稳定性的统计工具。艾伦方差提供了一种衡量频率或时间稳定性的方法，特别是在分析高精度时频信号，如原子钟或高精度振荡器的稳定性和噪声特性时非常有用。其数学公式定义为：

![艾伦方差公式](***

这里，y(τ)表示在时间间隔τ内的平均值，τ为采样间隔，T为总的测量时间，k为从1到T/τ的整数。σy(τ)计算了不同时间间隔τ下的平均频率偏差的标准差。

### 2.1.2 艾伦方差在噪声分析中的应用

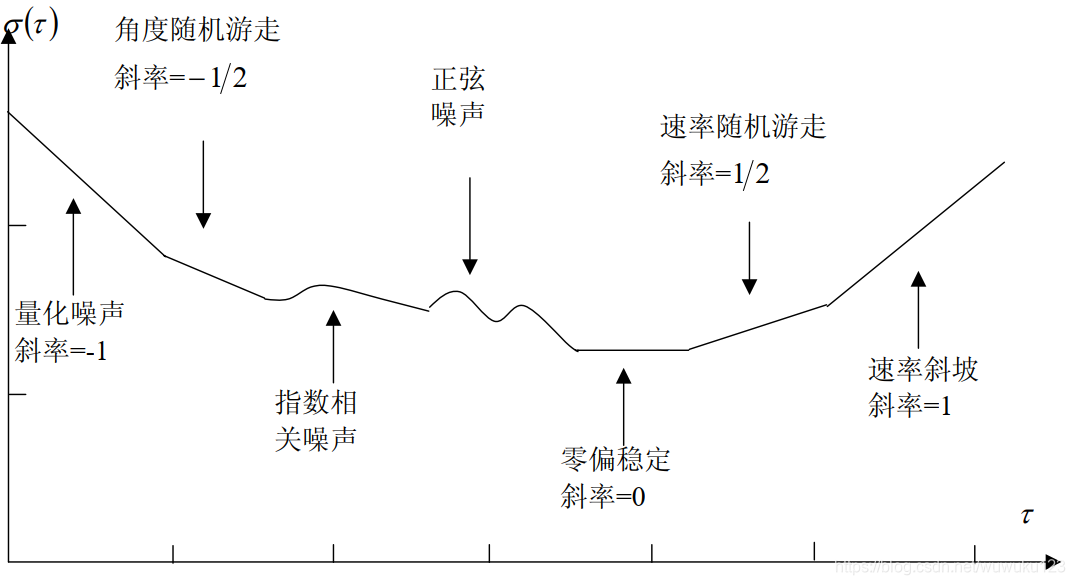
在噪声分析领域，艾伦方差允许我们区分并量化不同的噪声类型。例如，它可以帮助我们区分随机游走频率噪声、白相位噪声、闪变噪声等。通过艾伦方差图，我们可以识别出设备在不同时间尺度下的噪声特性，这对于设备设计和优化非常重要。

## 2.2 艾伦方差的计算方法

### 2.2.1 传统计算方法

传统上，艾伦方差的计算是基于观测到的频率或时间间隔数据。计算步骤通常包括：

1. 选择一个时间间隔τ，并计算所有可能的时间区间内平均频率值y(τ)。
2. 使用上式计算各个τ值下的艾伦方差。
3. 改变τ值，重复步骤1和2，绘制艾伦方差与τ的关系图。

### 2.2.2 MATLAB实现的优化计算步骤

使用MATLAB计算艾伦方差，我们可以利用内置的函数或编写自定义函数来实现。以下是使用MATLAB进行艾伦方差计算的步骤：

1. 收集频率数据：首先，我们获取MEMS陀螺仪的频率输出数据。
2. 数据预处理：数据可能需要预处理，例如去除异常值、进行平滑或滤波处理。
3. 编写计算艾伦方差的MATLAB函数：这个函数将根据公式递归计算不同τ下的σy(τ)。
4. 运行函数并绘制结果：将计算得到的艾伦方差数据绘制成图表，以分析设备的噪声特性。

下面是一个MATLAB代码块示例，该代码用于计算艾伦方差并绘制结果：

function allanvariance = allan_variance(data, taus)
    allanvariance = zeros(length(taus), 1);
    for i = 1:length(taus)
        tau = taus(i);
        allanvariance(i) = sum((data(2:end) - data(1:end-1)).^2) / (2 * (length(data) - 1) * tau^2);
    end
end

% 示例使用
% 假设data为时间序列数据，taus为一系列时间间隔
data = ...; % MEMS陀螺仪的频率输出数据
taus = [1, 10, 100, 1000]; % 预定义的时间间隔序列
allanvariance = allan_variance(data, taus);

% 绘制艾伦方差图
loglog(taus, allanvariance);
xlabel('Time Interval (s)');
ylabel('Allan Variance');
title('Allan Variance Plot');

## 2.3 艾伦方差分析的局限性与挑战

### 2.3.1 现有方法的局限性

尽管艾伦方差分析是一种强大的工具，但它也存在局限性。首先，它依赖于大量的稳定数据点，这对于快速变化的系统来说可能是一个挑战。其次，艾伦方差只能揭示某些类型的噪声，并不能区分所有可能的噪声源。

### 2.3.2 面临的挑战与未来发展方向

面对的挑战主要集中在如何进一步优化艾伦方差算法以适应更复杂的数据集，以及如何结合其他分析方法来增强噪声识别能力。未来的发展方向可能包括：

- 发展更加精细的噪声识别和分类算法。
- 将艾伦方差与其他统计方法结合，如小波变换或模糊逻辑。
- 利用机器学习和深度学习技术提高噪声分析的自动化和准确性。

# 3. MATLAB在MEMS陀螺仪噪声分析中的应用

MEMS陀螺仪作为导航、稳定和测量应用中的核心组件，其噪声特性直接影响设备的精确度和可靠性。噪声分析是评价MEMS陀螺仪性能的关键步骤，而MATLAB作为强大的数学计算和工程分析软件，为噪声分析提供了便捷而强大的工具。本章将详细讨论MATLAB在MEMS陀螺仪噪声分析中的应用。

## 3.1 MATLAB环境与工具箱介绍

### 3.1.1 MATLAB的安装和配置

MATLAB（Matrix Laboratory）是一款高性能的数值计算环境和第四代编程语言，广泛应用于数据分析、可视化、算法开发等领域。安装MATLAB的过程相对简单，用户仅需从MathWorks官方网站下载安装包，根据安装向导完成安装。安装完成后，需要进行配置以确保软件正常运行，包括设置环境变量、安装额外的工具箱等。

### 3.1.2 MATLAB中的信号处理工具箱

信号处理工具箱是MATLAB的核心扩展包之一，它提供了丰富的信号处理函数，覆盖了从信号的生成、分析到过滤、频谱分析等各个阶段。对于MEMS陀螺仪噪声分析而言，这些工具箱中的函数可以帮助工程师快速完成信号的时域分析、频域分析以及噪声特性评估等任务。

## 3.2 MATLAB处理MEMS陀螺仪数据的方法

### 3.2.1 数据预处理技巧

在进行噪声分析之前，需要对M