摘要
关键字
1. NURBS曲线积分计算基础
- 1.1 NURBS曲线数学基础
- 1.2 积分计算的数学模型
2. ```
第二章：云计算框架的理论架构

云计算-NURBS曲线相关积分量的计算.pdf

摘要

本文详细探讨了NURBS曲线积分计算在云计算框架中的应用基础、架构设计、实践搭建以及优化策略。首先介绍了NURBS曲线积分计算的数学基础及其在云计算框架理论架构中的原理。接着，文章阐述了云计算框架的设计原则、系统架构与技术选型，并详细说明了实践搭建过程中的部署环境准备、NURBS积分计算服务实现和性能调优。此外，还提出了NURBS曲线积分计算的优化策略，包括算法优化、资源管理和故障恢复与数据备份。最后，文章通过分析行业应用场景和成功案例，展望了云计算框架在未来面临的技术发展趋势、挑战和应对策略。

关键字

NURBS曲线；积分计算；云计算框架；性能调优；资源管理；故障恢复

参考资源链接：NURBS曲线积分计算：面积与弧长研究

1. NURBS曲线积分计算基础

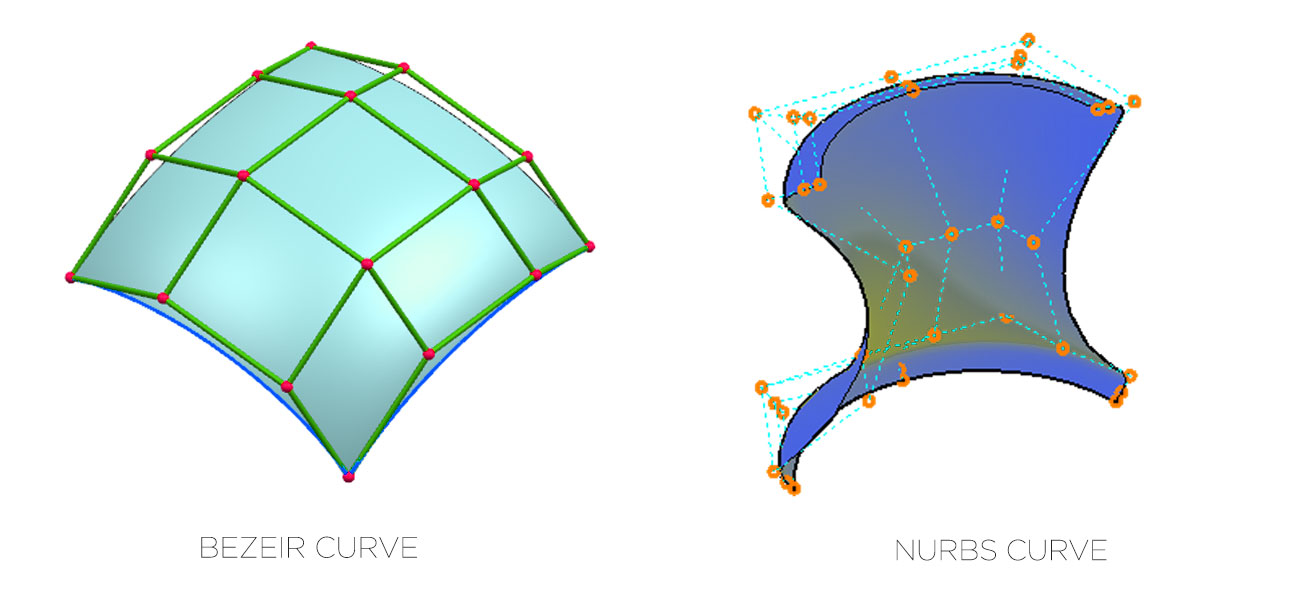
在现代工程和设计领域，非均匀有理B样条（NURBS）曲线积分计算是不可或缺的一部分，尤其在处理复杂的几何形状时。NURBS提供了一种灵活的数学模型，允许精确表示曲线、曲面，甚至是更复杂的自由形式的几何结构。积分计算是NURBS曲线解析中的核心，它涵盖了从基本的面积计算到更复杂的几何属性求解。

1.1 NURBS曲线数学基础

NURBS曲线是一种基于控制点的参数曲线，通过权重和节点向量的调整可以精确控制曲线的形状。数学表达式通常为：

1.2 积分计算的数学模型

在NURBS的上下文中，积分计算通常涉及对曲线上的特定函数进行积分。例如，我们可能会对曲线上的特定段落求面积或质量分布。在技术层面，这涉及到将曲线划分为小段并使用数值积分方法进行计算。例如，辛普森法则(Simpson’s rule)和高斯积分(Gaussian quadrature)都是常用的数值积分方法。一个简单的积分示例代码如下：

import numpy as np
# 定义一个函数，比如 NURBS 曲线的密度函数
def density_function(x):
    return x**2
# 使用辛普森法则计算定积分
def simpson_rule(a, b, n, func):
    h = (b - a) / n
    x = np.linspace(a, b, n + 1)
    y = func(x)
    S = h/3 * (y[0] + 4 * np.sum(y[1:-1:2]) + 2 * np.sum(y[2:-2:2]) + y[-1])
    return S
# 计算区间 [a, b] 上的定积分
a = 0
b = 1
n = 100  # 分割区间数量
integral = simpson_rule(a, b, n, density_function)
print("积分结果:", integral)

这个简单的代码示例展示了如何用辛普森法则近似计算一个简单函数的定积分。在实际应用中，NURBS曲线积分计算会更复杂，涉及更多的数学和编程技巧。通过理解基础，我们可以逐步深入到更高级的应用和优化技术。

2. ```

第二章：云计算框架的理论架构

云计算技术已经成为现代IT架构不可或缺的一部分，它的设计原则和系统架构对性能、可扩展性和维护性都有着深远的影响。本章将深入探讨云计算框架的设计原则、系统架构以及技术选型的诸多细节，展示云计算框架如何适应不同业务需求的挑战。

2.1 NURBS曲线积分算法原理

NURBS曲线积分算法是云计算框架中经常遇到的一类算法问题。理解其原理对于云计算框架的设计至关重要。

2.1.1 NURBS曲线数学基础

NURBS（Non-Uniform Rational B-Spline）是一种用于计算机图形学中描述复杂曲面的数学模型。它由一系列控制点定义，通过非均匀理性B样条曲线来表示。计算NURBS曲线的积分是评估曲线上某一部分的几何属性（如长度、面积等）的关键步骤。在云计算环境中，这项任务可能需要处理海量的数据点，因此算法的效率至关重要。

2.1.2 积分计算的数学模型

积分计算在NURBS曲线处理中一般通过数值方法实现，如高斯-勒让德（Gauss-Legendre）积分或者辛普森（Simpson）积分法。在云计算框架中，如何有效地分配计算资源和优化算法执行，是设计高性能积分计算服务时需要考虑的。

2.2 云计算框架的设计原则

云计算框架的设计需要遵循一系列原则，以确保服务的可靠性、弹性和可管理性。

2.2.1 云计算技术概述

云计算技术的核心在于提供按需的资源供应和服务交付。它涉及资源池化、虚拟化、自动化管理和服务接口等多个方面。设计云计算框架时，需要考虑如何将这些技术整合以满足多样化的用户需求。

2.2.2 框架设计中的关键考虑因素

云计算框架的设计应考虑到服务的可伸缩性、安全性、性能以及成本效率。框架设计者需要平衡这些因素，以提供一个高性能且用户友好的云服务环境。

2.3 系统架构与技术选型

一个高效的云计算框架需要一个结构合理的系统架构，并选择适当的技术栈和工具。

2.3.1 架构组件与服务

云计算框架的架构通常包括计算、存储、网络等基础资源层，以及服务管理层、用户接口层等。每个组件都应该设计成可以独立伸缩，以便更好地适应不同的工作负载。

2.3.2 技术栈和工具的选择

技术栈的选择会影响系统的整体性能和运维复杂度。例如，可以选择Kubernetes作为容器编排工具，以实现自动化部署和管理。同时，还需要考虑监控、日志记录、安全、身份验证和授权等工具的集成。


# 3. 云计算框架的实践搭建
在理解了云计算框架的理论架构和NURBS曲线积分计算基础之后，本章节将聚焦于如何将这些概念转化为实践，并搭建一个切实可用的云计算框架。我们将逐步探讨从硬件资源的配置到软件环境的搭建，再到具体服务实现及性能调优的全过程。
## 3.1 部署环境准备
部署环境的准备工作是云计算框架搭建的基础，它涉及到硬件资源的配置和软件环境的搭建。
### 3.1.1 硬件资源的配置
硬件资源的配置需要根据云计算框架的规模和预期负载进行合理规划。通常包括以下几个方面：
- **服务器配置**：包括CPU、内存、存储和网络接口卡等，需根据工作负载的计算密集型或I/O密集型特点进行选择。
- **存储解决方案**：可采用传统的SAN/NAS存储或更为现代的分布式存储系统，考虑数据冗余和高可用性。
- **网络设计**：网络带宽、交换机、路由器等设备的选择要确保低延迟和高吞吐量，以满足大量并发请求的需求。
在实际操作中，可利用虚拟化技术将物理资源抽象化，以提高资源利用率和灵活性。
### 3.1.2 软件环境的搭建
软件环境的搭建包括操作系统、中间件、开发工具和监控工具的安装与配置。对于云计算框架来说，以下软件是关键部分：
- **操作系统选择**：Linux是大多数云环境的首选，以其稳定性和社区支持而闻名。
- **容器化技术**：Docker容器和Kubernetes集群管理系统是构建微服务架构的基石。
- **编程语言和框架**：根据服务需求选择合适的编程语言和Web框架，如Python、Go、Java等。
- **数据库和缓存系统**：选择适当的数据库（如MySQL、MongoDB）和缓存系统（如Redis），以支持高效的数据访问和存储。
例如，创建一个基于Python Flask的简单Web服务，可以使用Docker容器进行封装，确保应用的可移植性和一致性。
```bash
# Dockerfile 示例代码块
FROM python:3.8-slim
WORKDIR /usr/src/app
COPY requirements.txt ./
RUN pip install --no-cache-dir -r requirements.txt
COPY . .
CMD [ "python", "./app.py" ]

该代码块说明了如何创建一个Docker镜像来部署一个Python应用，其中requirements.txt列出了所有必需的Python库。

3.2

最低0.47元/天解锁专栏

买1年送1年

点击查看下一篇

百万级高质量VIP文章无限畅学

千万级优质资源任意下载

C知道免费提问 ( 生成式Al产品 )

构建高效NURBS曲线积分计算：云计算框架的设计与实施细节

摘要

关键字

1. NURBS曲线积分计算基础

1.1 NURBS曲线数学基础

1.2 积分计算的数学模型

2. ```

第二章：云计算框架的理论架构