【射频通信的幕后英雄】：相敏检波在无线信号处理中的关键角色


# 摘要
射频通信技术在无线信号处理领域具有核心作用，而相敏检波作为其关键技术之一，广泛应用于无线通信系统中。本文首先介绍了射频通信的基础知识和相敏检波的理论基础，包括其定义、工作原理、数学模型及信号分析。随后，文章探讨了相敏检波在无线信号处理中的实际应用，例如无线信号的解调和还原、提升信号传输质量，以及其硬件实现的挑战与优化方法。此外，本文还对相敏检波在现代通信系统，如5G和物联网通信中的高级应用进行了阐述，并对未来发展和潜在挑战进行了预测和分析。最后，文章总结了相敏检波的重要性，并对其未来的发展方向提出了展望。

# 关键字
射频通信；相敏检波；信号处理；无线通信；硬件设计；未来趋势

参考资源链接：[相敏检波电路-(幅值调制信号的解调)](https://wenku.csdn.net/doc/6412b640be7fbd1778d460fb?spm=1055.2635.3001.10343)
# 1. 射频通信基础

射频通信是现代无线通信不可或缺的一部分，它覆盖了从微波到毫米波的宽广频段。在深入探讨相敏检波之前，有必要先了解射频通信的基础知识。射频信号因其传输速度快、覆盖范围广而被广泛应用于各种通信系统中，例如无线局域网(Wi-Fi)、蜂窝移动通信、卫星通信等。

## 1.1 射频信号的特征
射频信号是电磁波的一种形式，其频率范围通常在300kHz到300GHz之间。在通信系统中，射频信号承载着信息，通过调制技术在不同的频率、相位或幅度上携带数据。

## 1.2 射频通信的工作原理
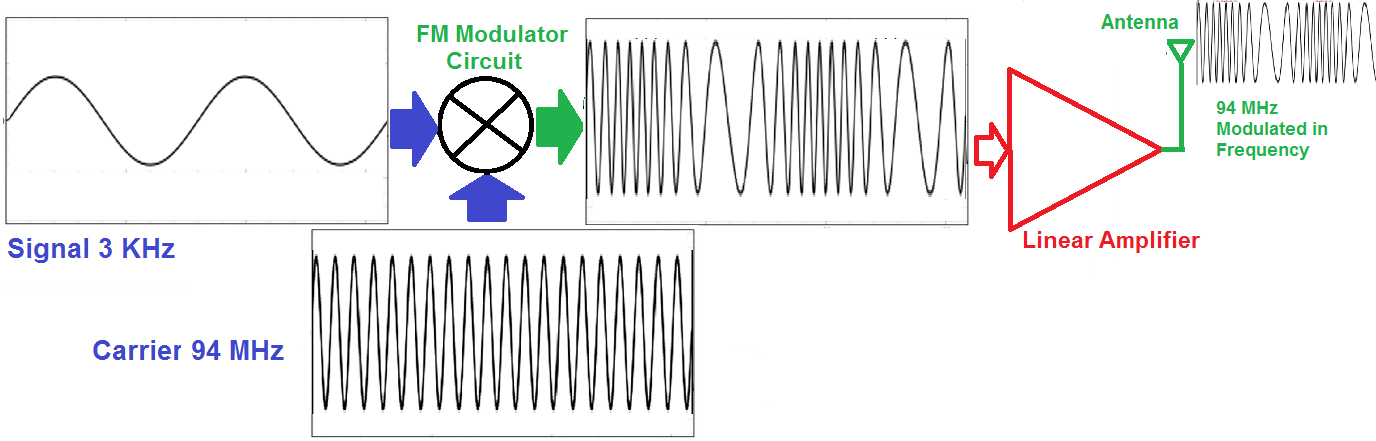
在射频通信中，信息通过调制过程嵌入到载波信号中。调制技术的选用基于通信需求，常见的调制方式包括调幅(AM)、调频(FM)和调相(PM)。调制后的信号通过发射机发送，接收机再将其解调还原成原始信息。

## 1.3 射频通信系统的关键组件
射频通信系统包括天线、调制器、发射机、接收机、解调器等部分。天线负责发送和接收射频信号，调制器和发射机负责将信息信号调制到高频载波上，而接收机和解调器则执行相反的过程。

射频通信是相敏检波技术应用的前提，理解这些基础知识是后续章节深入探讨相敏检波的前提条件。

# 2. 相敏检波的理论基础

### 2.1 相敏检波的定义和工作原理
#### 2.1.1 相敏检波的定义

相敏检波是一种信号处理技术，主要用于提取调制信号中的信息。它依据输入信号和参考信号之间的相位关系来检测和放大特定频率成分的信号。这一过程通常涉及到将调制信号与一个参考信号（本地振荡器信号）相乘，然后通过低通滤波器来获得调制信号的包络或基带信息。相敏检波在无线通信、雷达系统和锁相环等领域有着广泛的应用。

#### 2.1.2 相敏检波的工作原理

相敏检波的过程可以分为以下几个步骤：

1. **信号乘法**：首先，输入的调制信号与一个本地振荡器（LO）产生的参考信号进行相乘。这个参考信号通常是未调制的正弦波，并且与调制信号有着相同的频率但不同的相位。

2. **信号过滤**：相乘之后，得到的产物通过一个低通滤波器（LPF）。低通滤波器的作用是移除乘积信号中的高频分量，保留与原始调制信号相对应的频率分量。这个步骤是相敏检波的关键，因为它决定了最终能够提取的信息内容。

3. **信号提取**：通过低通滤波后的信号是原始调制信号的包络表示，包含了调制信号的全部信息。根据输入信号和本地振荡器信号的相位差，输出信号可以是原始调制信号的原信号、反相信号或者它们的组合。

### 2.2 相敏检波的数学模型和信号分析
#### 2.2.1 相敏检波的数学模型

为了更深入地理解相敏检波的工作原理，我们可以构建一个简单的数学模型来模拟这一过程。假设一个调制信号可以表示为：

\[ m(t) = A_m \cos(2\pi f_m t + \phi_m) \]

其中，\( A_m \) 是调制信号的振幅，\( f_m \) 是调制信号的频率，而 \( \phi_m \) 是调制信号的初始相位。本地振荡器信号表示为：

\[ l(t) = A_l \cos(2\pi f_l t + \phi_l) \]

其中，\( A_l \) 是本地振荡器信号的振幅，\( f_l \) 是本地振荡器信号的频率，而 \( \phi_l \) 是本地振荡器信号的初始相位。这两个信号相乘，我们得到：

\[ x(t) = m(t) \times l(t) = A_m A_l \cos(2\pi f_m t + \phi_m) \cos(2\pi f_l t + \phi_l) \]

利用三角恒等变换，\( x(t) \) 可以被进一步简化，之后通过低通滤波器我