Delta-Sigma调制器设计必知：模拟电路与量化噪声处理


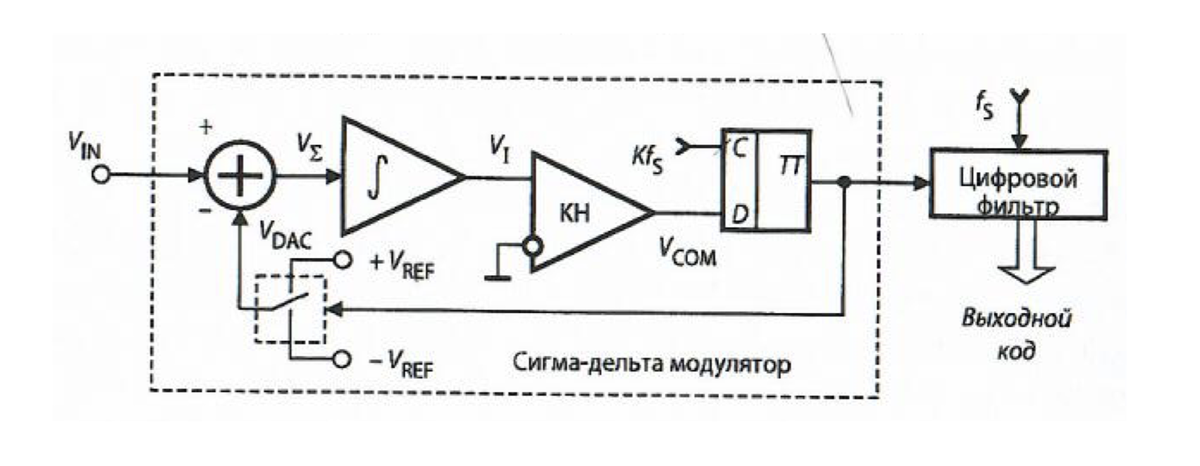
# 摘要
Delta-Sigma调制器作为高性能的模拟至数字转换技术，在音频处理、通信以及数据采集系统等领域有着广泛的应用。本文首先概述了Delta-Sigma调制器的基本原理和作用，然后详细讨论了模拟电路设计基础，包括信号与系统分类、设计原则、模拟滤波器设计及其调制解调技术。进而，文章深入分析了量化噪声的理论基础及其与信号处理的关系，并探讨了高级量化噪声处理技术。在设计实践部分，本文介绍了调制器设计流程、实现细节和优化技巧，以及实验验证与调试方法。最后一章着眼于Delta-Sigma调制器的现代应用，探讨其在音频与通信领域的应用案例，数据采集系统的性能评估及芯片级集成的挑战与发展方向。

# 关键字
Delta-Sigma调制器；模拟电路设计；量化噪声；数字信号处理；数据采集系统；芯片集成

参考资源链接：[Delta-Sigma调制详解：从入门到精通](https://wenku.csdn.net/doc/6412b484be7fbd1778d3fdba?spm=1055.2635.3001.10343)
# 1. Delta-Sigma调制器概述

Delta-Sigma调制器是一种高效的信号处理技术，广泛应用于高精度模拟信号的转换。通过超量化的噪声整形，它在数字音频设备、无线通信和传感器接口中发挥着关键作用。Delta-Sigma调制器的基本工作原理是通过差分编码和积分处理来提高信号的精度，从而减少量化误差并达到更高的信噪比。

在这一章节中，我们将从Delta-Sigma调制器的起源、工作原理和其在现代电子系统中的应用背景开始，逐步深入理解其结构和功能。此外，我们将探讨它如何通过过采样和噪声整形技术来提高信号质量，以及它与其他调制技术相比的优势所在。本章节旨在为读者提供一个全面的理解框架，为深入研究后续章节做好铺垫。

# 2. 模拟电路基础与设计

### 2.1 模拟电路基本概念

#### 信号与系统的分类

在模拟电路设计中，信号与系统的分类是基础。信号可以分为模拟信号和数字信号两种。模拟信号是连续的，能够在时间上和振幅上连续取值。数字信号则是离散的，时间和振幅上的取值都是经过量化的。

系统按照其处理信号的方式来分类，可以分为线性系统和非线性系统。线性系统遵循叠加原理，即系统的输出对于输入信号的线性组合等于这些信号分别输入系统时输出的线性组合。而非线性系统则不满足这一原理。在设计模拟电路时，通常需要保证电路的线性度，以满足信号处理的需求。

在设计模拟电路时，必须熟悉信号与系统的分类以及它们之间的相互作用。这有助于选择合适的电路拓扑和元件，以实现预期的电路功能。

### 2.2 模拟滤波器设计

#### 滤波器的类型和应用

滤波器是模拟电路中非常重要的组件之一，用于允许特定频率的信号通过而阻碍其它频率信号。常见的滤波器类型包括低通、高通、带通和带阻滤波器。

低通滤波器允许低于某一截止频率的信号通过，而阻止高于该截止频率的信号。高通滤波器则相反，阻止低于截止频率的信号。带通滤波器允许某一特定频率范围内的信号通过，而带阻滤波器则阻止这一频率范围内的信号。

模拟滤波器在电子设备中有着广泛的应用，比如在音频处理设备中用来去除噪声，或者在通信设备中用于频率选择。

#### 滤波器设计的具体步骤

设计一个模拟滤波器通常包括以下几个步骤：

1. **需求分析**：首先确定滤波器的类型（低通、高通、带通、带阻），以及通带和阻带的要求。
2. **选择滤波器类型**：根据需求分析的结果选择合适的滤波器类型。
3. **确定电路拓扑**：根据所需的滤波性能选择适当的电路拓扑结构，如巴特沃斯、切比雪夫、贝塞尔等。
4. **计算元件值**：使用滤波器设计的数学公式和设计图表，计算电路中所需的电阻、电容和电感等元件的数值。
5. **电路仿真**：在仿真软件中搭建电路模型，验证设计的滤波器是否符合预期性能。
6. **实际搭建与测试**：在实验板上搭建实际电路，并使用仪器进行测试，确保电路在实际条件下能够正常工作。

### 2.3 模拟信号的调制与解调

#### 调制技术的基本原理

调制是通过改变某一信号（载波）的某些特性（幅度、频率、相位）来传递另一信号信息的过程。在模拟信号调制中，最常见的是幅度调制（AM）、频率调制（FM）和相位调制（PM）。

幅度调制是通过改变载波的幅度来表示信息信号的幅度。频率调制则是改变载波的频率来传递信息。相位调制通过改变载波的相位来传递信息。这些调制技术使得信号能够在无线电波中高效传输，是通信系统设计的核心部分。

#### 解调技术的应用实例

解调是调制过程的逆过程，目的是从已调制的信号中提取出原始信息。解调器是实现解调的关键组件。

一个应用实例是无线通信接收机中的超外差解调器。它通过将接收到的调制信号转换为一个固定的中频信号来简化信号处理，从而实现对原始信息的恢复。超外差解调器的一个关键优势是能够在较宽的频率范围内进行有效接收，使得单个接收机能够覆盖多个频段。

在设计解调电路时，通常需要考虑到信号的灵敏度、选择性和动态范围等因素，以及如何最大化信噪比。实际电路设计中，解调器的实现通常包括放大器、混频器、滤波器和检波器等组件。

在这一章节中，我们详细探讨了模拟电路的基本概念、滤波器设计以及调制与解调技术，为理解更高级的信号处理技术打下了坚实的基础。接下来的章节将深入探讨量化噪声与信号处理，以及Delta-Sigma调制器设计实践。

# 3. 量化噪声与信号处理

量化噪声是数字信号处理中一个重要的概念，其产生于模拟信号被数字化的过程中。本章节将深入探讨量化噪声的理论基础、信号的数字化处理方法以及如何应用高级量化噪声处理技术。

#### 3.1 量化噪声的基本理论

##### 3.1.1 量化噪声的来源与特性

量化噪声产生于模拟信号转换为数字信号时由于位数限制引起的误差。当模拟信号通过模数转换器（ADC）时，由于数字系统位数的限制，信号会被切割成有限个离散电平，无法完全精确地表示原始信号，这种由量化步长引起的误差就是量化噪声。

量化噪声的主要特性包括它的统计特性、功率谱密度和对信号的影响。量化噪声通常被视作在频域上均匀分布的白噪声，其功率谱密度与信号频率无关。量化噪声的幅值与ADC的分辨率（位数）密切相关；分辨率越高，量化步长越小，噪声水平越低，信噪比越高。

\text{信噪比(SNR)} = 6.02n + 1.76 \text{dB}

其中