【关键作用】数理统计在数据分析中的5大应用，让你的数据说话！


# 摘要
本文综述了数理统计基础及其在数据分析中的应用，涵盖了描述性统计分析、推断性统计方法、预测模型与数据挖掘技术，以及数理统计在金融、生物统计学和社会科学研究中的特定应用。首先，介绍了描述性统计的基本概念，如中心趋势与离散程度的度量，数据分布的探索和数据可视化技术。接着，探讨了推断性统计中假设检验、参数估计以及相关性与回归分析的方法。第三章阐述了时间序列分析、分类与聚类分析以及关联规则与数据降维。最后，文章针对金融数据分析、生物统计学应用及社会科学研究中的实际案例，探讨了数理统计的深入应用，旨在提供理论与实践相结合的分析框架。

# 关键字
数理统计；描述性统计；推断性统计；预测模型；数据挖掘；金融数据分析；生物统计学；社会科学研究

参考资源链接：[《应用数理统计》钟波等著课后答案解析](https://wenku.csdn.net/doc/u90j92zqn7?spm=1055.2635.3001.10343)
# 1. 数理统计基础与数据分析概述

数据分析是挖掘数据背后隐藏信息的过程，它的核心是数理统计。数理统计通过建立模型来描述和预测数据的变化，是数据分析的基础工具。在这一章，我们将首先介绍数理统计的基础知识，包括统计学的定义、它的历史以及在现实世界中的应用。我们还将概述数据分析的基本概念，包括数据收集、处理和解释的流程。此章节的目标是为读者构建一个坚实的理论基础，为深入理解后续章节的高级统计方法和数据分析技术打下基础。在此基础上，我们将介绍数据分析流程中的关键步骤，包括数据清洗、数据转换和数据探索，为接下来深入分析具体案例做好准备。

# 2. 描述性统计分析

## 2.1 描述性统计基本概念

### 2.1.1 中心趋势的度量

中心趋势是描述性统计分析中用来反映数据集中趋势的一个重要概念，它能够提供数据集中典型值的信息。常见的中心趋势度量有三种：均值、中位数和众数。

#### 均值（Mean）
均值是最常见的中心趋势度量，它通过将所有数据值相加后除以数据的总个数得到。公式可以表示为：

\[ \bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_{i} \]

其中，\(\bar{x}\)表示均值，\(x_{i}\)代表数据集中的每一个数据点，而\(n\)是数据点的总个数。

#### 中位数（Median）
中位数是指将数据集进行排序后处于中间位置的数值。如果数据点的数量是奇数，则直接取中间的数值；如果是偶数，则取中间两个数值的平均值。中位数对极端值不敏感，因此它在描述偏斜数据集的中心趋势时比均值更加可靠。

#### 众数（Mode）
众数是指数据集中出现次数最多的数值。在一组数据中，众数可以不唯一，也可以不存在（当所有数值出现的次数相同时）。

### 2.1.2 离散程度的度量

离散程度是衡量数据点分布范围的一个统计度量，反映了数据的变异性。常见的离散程度度量包括极差、方差和标准差。

#### 极差（Range）
极差是数据集中最大值与最小值之间的差值。计算公式为：

\[ \text{Range} = \max(x) - \min(x) \]

其中，\(\max(x)\)和\(\min(x)\)分别是数据集中的最大值和最小值。

#### 方差（Variance）
方差是各个数据点与均值差值的平方的平均数，用来衡量数据点分布的离散程度。其计算公式为：

\[ \sigma^{2} = \frac{1}{n}\sum_{i=1}^{n}(x_{i} - \mu)^{2} \]

其中，\(\sigma^{2}\)表示方差，\(\mu\)是数据集的均值，\(x_{i}\)是数据集中的每一个数据点。

#### 标准差（Standard Deviation）
标准差是方差的平方根，它具有与原始数据相同的单位，因此更便于解释。计算公式为：

\[ \sigma = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_{i} - \mu)^{2}} \]

其中，\(\sigma\)表示标准差，其他符号意义同前。

## 2.2 数据分布的探索

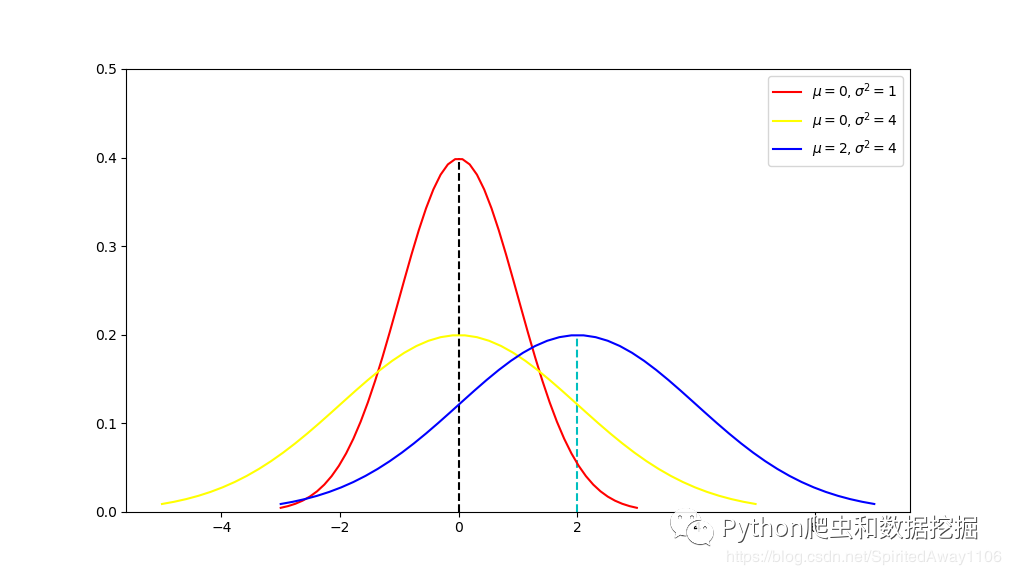
### 2.2.1 正态分布及其特性

正态分布（Normal Distribution），也称为高斯分布（Gaussian Distribution），是一种非常重要的连续概率分布，其图形呈现为钟形曲线。正态分布在自然科学和社会科学的许多现象中广泛出现，是许多统计分析的基础。

#### 正态分布的特点
- 正态分布的曲线完全对称，其均值、中位数和众数都位于曲线的中心，且三者重合。
- 曲线在均值附近较高，曲线两端逐渐降低并趋近于横轴，但永远不会与横轴相交。
- 正态分布的形状由两个参数决定，即均值（μ）和标准差（σ）。

#### 应用
在数据分析中，许多统计方法都假设数据服从正态分布。例如，在进行假设检验时，检验数据的分布是否符合正态分布是一个重要的前提条件。如果数据符合正态分布，那么可以使用诸如Z检验或t检验这样的参数检验方法。

### 2.2.2 偏态与峰态分析

偏态（Skewness）和峰态（Kurtosis）是描述数据分布形状的两个重要指标，它们帮助我们了解数据分布的不对称性和集中程度。

#### 偏态
偏态描述了数据分布的不对称性。当分布的尾部左侧更长时，称分布是左偏（负偏态）；当尾部右侧更长时，称分布是右偏（正偏态）。偏态的计算公式为：

\[ \text{Skewness} = \frac{E[(X-\mu)^3]}{\sigma^3} \]

其中，\(E\)表示期望值，\(X\)是随机变量，\(\mu\)是均值，\(\sigma\)是标准差。

#### 峰态
峰态描述了数据分布的尖峭或平坦程度。与正态分布相比，如果数据分布更加尖峭，则称其为尖峰（高峰态）；如果数据分布更平坦，则称其为平峰（低峰态）。峰态的计算公式为：

\[ \text{Kurtosis} = \frac{E[(X-\mu)^4]}{\sigma^4} - 3 \]

其中，各项符号意义同前，而减去3是为了使正态分布的峰态值为0。

## 2.3 数据可视化技术

### 2.3.1 统计图表的类型与选择

数据可视化是数据分析的重要组成部分，它以图形的方式直观表达数据信息，使观察者更容易理解数据。常见的统计图表包括柱状图、饼图、折线图、箱形图等。

#### 柱状图（Bar Chart）
柱状图适用于展示各类别数据的数量对比。每个柱子的长度表示数据的大小，常用于展示分类数据的分布情况。

#### 饼图（Pie Chart）
饼图用来表示不同类别数据占总体的比例关系。它将数据集分割为大小不同的扇形区域，每个区域的角度大小与数据类别所占的比例成正比。

#### 折线图（Line Chart）
折线图能够展示数据随时间或其他连续变量变化的趋势。它由数据点连接而成的折线表示，适用于时间序列数据。

#### 箱形图（Box Plot）
箱形图展示了一组数据的五数概括（最小值、第一四分位数、中位数、第三四分位数、最大值），以及异常值。它能够提供数据分布的中心位置、离散程度、偏态等信息。

### 2.3.2 高级数据可视化工具与实践

随着大数据的发展，出现了许多高级的数据可视化工具，如Tableau、Power BI、R语言的ggplot2包、Python的Matplotlib和Seaborn库等。这些工具能够处理复杂的数据集，并提供丰富的图表类型以及交互式可视化功能。

#### Tableau
Tableau是一款非常受欢迎的商业智能软件，它提供了强大的数据连接、处理和可视化功能。用户可以通过拖放界面快速创建交云动式数据仪表板。

#### R语言的ggplot2包
ggplot2是R语言中一个非常强大的绘图包，它基于“图形语法”（Grammar of Graphics），使得创建复杂的数据可视化变得简单而直观。

#### Python的Matplotlib和Seaborn库
Matplotlib是Python中最基础的绘图库，而Seaborn是在Matplotlib基础上扩展的，它提供了一系列高级接口，能够更美观、更高效地进行数据可视化。

### 代码块示例与分析

下面代码块展示如何使用Python的matplotlib库和seaborn库创建一个简单的箱形图：

import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd

# 创建一个示例数据框
data = pd.DataFrame({
    'Category1': [10, 12, 12, 13, 12, 10, 14],
    'Category2': [15, 15, 13, 14, 16, 15, 12]
})

# 绘制箱形图
sns.boxplot(data=data)
plt.title('Box Plot Example')
plt.show()

在此代码中，首先导入必要的库，然后创建一个包含两列数据的数据框`data`。接着使用Seaborn库中的`boxplot`函数绘制箱形图，并通过`plt.title`添加标题。最后，使用`plt.show()`函数将图表展示出来。

通过上述步骤，我们能够直观地看到每列数据的分布情况，包括中位数、四分位数以及可能存在的异常值。数据可视化不仅仅是为展示美观，更重要的是帮助我们从数据中挖掘信息，进行更深入的分析。

以上是第二章的详细内容。在后续的章节中，我们将继续深入探讨统计分析的其他重要主题，包括推断性统计方法、预测模型、数据挖掘以及数理统计在特定领域的应用等。

# 3. ```markdown
# 第三章：推断性统计方法在数据分析中的应用

## 3.1 假设检验基础
### 3.1.1 假设检验的基本步骤
假设检验是推断性统计方法的核心，它允许我们根据样本数据对总体参数做出推断。基本步骤包括：

1. 提出零假设（H0）和对立假设（H1）。零假设通常表示没有效应或者差异，而对立假设表示有某种效应或差异。
2. 选择显著性水平（α），这通常是0.05或0.01，决定了错误拒绝零假设的风险阈值。
3. 计算检验统计量，这是从样本数据中获得的值，用于比较观察到的数据与零假设下的理论数据。
4. 做出决策：如果计算出的统计量落在了拒绝域内（通常与p值相关），则拒绝零假设；否则，没有足够的证据拒绝零假设。

### 3.1.2 常用的假设检验方法
在数据分析中，根据数据的类型和分布，会选择不同的假设检验方法：

- Z检验：适用于大样本量（n>30）且总体标准差已知的情况。
- T检验：用于样本量较小且总体标准差未知的情况，有单样本T检验、配对样本T检验和独立样本T检验。
- 卡方检验：用于分类数据，检验样本分布是否与总体分布一致。
- 方差分析（ANOVA）：用于比较三个或以上的样本均值，检验组间是否存在显著差异。

## 3.2 参数估计
### 3.2.1 点估计与区间估计
参数估计是指用样本来估计总体的参数。点估计和区间估计是最常用的两种估计方法。

- 点估计：使用样本统计量（如样本均值、样本方差）直接作为总体参数的估计值。
- 区间估计：给出一个区间，这个区间以一定的概率包含总体参数。常见的区间估计方法有置信区间。置信区间的宽度受样本量、置信水平和总体方差的影响。

### 3.2.2 估计方法的选择与评估
在选择合适的参数估计方法时，需要考虑以下因素：

- 数据类型和分布：根据数据是否是连续还是分类以及其分布特征来选择估计方法。
- 样本量：小样本量可能需要使用t分布，而大样本量则可以用z分布。
- 精确度和置信水平：通常需要权衡置信水平和置信区间的宽度，更高置信水平会产生更宽的区间。

## 3.3 相关性与回归分析
### 3.3.1 相关性的概念与度量
相关性分析用于衡量两个变量之间是否存在某种统计联系，以及联系的强度。

- 皮尔逊相关系数（Pearson correlation coefficient）：用于衡量连续变量之间的线性相关性，取值范围在-1到1之间。
- 斯皮尔曼等级相关系数（Spearman's rank correlation coefficient）：用于衡量变量的单调关系，不要求数据服从正态分布。

### 3.3.2 线性回归模型及其应用
回归分析是一种用于研究变量间关系的统计工具，其中最简单的是线性回归模型：

- 简单线性回归：研究一个自变量与一个因变量之间的线性关系。
- 多元线性回归：扩展到两个或多个自变量，以研究它们与一个因变量之间的关系。

线性回归模型可应用在：

- 预测分析：例如，基于广告支出预测销售额。
- 因果关系研究：例如，研究教育水平与收入之间的关系。

在实际应用中，需要检验模型的假设，进行诊断分析，评估模型的拟合度，并进行必要的预测。

# 4. ```
# 第四章：预测模型与数据挖掘

在数据分析的世界中，预测模型与数据挖掘是关键手段，用以从历史数据中洞察未来趋势，并从大量数据中提取有意义的模式。本章将深入探讨时间序列分析、分类与聚类分析以及关联规则与数据降维等关键主题。

## 4.1 时间序列分析

### 4.1.1 时间序列数据的类型和特点

时间序列分析是利用数据的时间顺序来识别其中的模式、周期性和趋势等特征。时间序列数据通常分为以下几种类型：

- 平稳时间序列：数据的统计特性不随时间变化。
- 非平稳时间序列：数据的统计特性随时间变化，常常需要进行差分或转换来达到平稳状态。
- 季节性时间序列：数据呈现出重复的周期性波动。
- 循环时间序列：比季节性更长周期的时间序列波动，往往与经济周期相关联。

时间序列分析的特点主要包括：

- 时间依赖性：相邻观测值之间的相互关系。
- 趋势性：时间序列整体向上或向下移动的特征。
- 周期性：数据随时间呈周期性变化的特性。
- 不规则性：由随机波动或异常值引起的数据波动。

### 4.1.2 时间序列预测方法介绍

时间序列预测方法可以帮助我们根据历史数据来预测未来值。常见的方法包括：

- 移动平均法：通过计算过去几个时期的平均值来预测下一个时期的值。
- 指数平滑法：为每个观测值分配一个衰减因子，使得近期的数据具有更大的权重。
- ARIMA模型（自回归积分滑动平均模型）：一种结合了自回归模型和滑动平均模型的统计模型，用于分析和预测时间序列数据。

以下是使用Python进行简单移动平均预测的一个例子：

import numpy as np
import matplotlib.pyplot as plt

# 假设这是我们的月度销售额数据
sales = np.array([23, 24, 22, 26, 28, 26, 32, 33, 31, 35, 38, 37])

# 使用3个月的移动平均来预测
def moving_average(series, n):
"""计算移动平均
:param series: 时间序列数据
:param n: 移动平均的时期数
:return: 预测值列表
"""
predictions = []
for i in range(len(series) - n + 1):
this_window = series[i:i + n]
avg = np.mean(this_window)
predictions.append(avg)
return predictions

# 3个月移动平均
predictions = moving_average(sales, 3)

# 绘制图形
plt.figure(figsize=(10, 5))
plt.plot(sales, label="Actual")
plt.plot(predictions, label="Predicted")
plt.legend()
plt.show()

## 4.2 分类与聚类分析

### 4.2.1 分类算法的原理与应用

分类是数据挖掘中的一个主要任务，目的是利用历史数据构建模型来预测新数据的类别。分类算法通常包括：

- 决策树：一种树形结构，每个内部节点表示一个属性上的测试，每个分支代表测试结果，每个叶节点代表一种类别。
- 随机森林：基于多个决策树的集成学习方法，每棵树是独立生成的，对于分类结果进行投票。
- 支持向量机（SVM）：通过寻找最优超平面来将数据分类，使得不同类别之间的间隔最大化。

### 4.2.2 聚类分析的常用方法与实例

聚类分析的目的是将数据分为多个组或“簇”，使得同一簇中的数据点彼此相似，而与其他簇中的数据点不同。常见的聚类算法有：

- K-均值：一种划分方法，通过迭代更新簇的中心点来最小化簇内距离平方和。
- 层次聚类：一种建立层次化簇结构的方法，分为凝聚式（自底向上）和分裂式（自顶向下）。
- DBSCAN：一种基于密度的空间聚类算法，能够识别任意形状的簇。

在进行聚类分析时，我们通常要选择合适的距离度量方式，比如欧几里得距离、曼哈顿距离等。以下是一个使用Python中的K-means聚类算法的例子：

from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt

# 随机生成一些数据点
X = np.random.rand(100, 2)

# 选择两个簇中心
kmeans = KMeans(n_clusters=2, random_state=0).fit(X)

# 打印簇中心点坐标
print(kmeans.cluster_centers_)

# 将数据点的簇标签绘制出来
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
plt.show()

## 4.3 关联规则与数据降维

### 4.3.1 关联规则挖掘的基本原理

关联规则挖掘旨在在大型事务数据库中发现不同变量之间的有趣关系。这一过程一般分为两步：

- 规则发现：使用算法找出频繁项集。
- 规则生成：从频繁项集中生成强关联规则。

最著名的关联规则挖掘算法是Apriori算法。它通过逐层搜索频繁项集的方法来挖掘关联规则。

### 4.3.2 数据降维技术的介绍与应用

数据降维是减少数据集中变量的数量的过程，同时尽量保留数据集的主要特征和结构。常用的数据降维技术包括：

- 主成分分析（PCA）：一种统计方法，通过正交变换将数据转换为一组线性不相关的变量（主成分）。
- t-SNE（t-distributed Stochastic Neighbor Embedding）：一种非线性降维技术，特别适合高维数据的可视化。
- 线性判别分析（LDA）：一种统计方法，旨在找到最佳的特征空间，使得类间差异最大化，类内差异最小化。

通过降维，我们可以降低模型的复杂性，加快计算速度，同时也能够提高模型的泛化能力。以下是利用PCA进行数据降维的一个例子：

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA

# 加载Iris数据集
iris = load_iris()
X = iris.data
y = iris.target

# 应用PCA，降维至2维
pca = PCA(n_components=2)
X_r = pca.fit_transform(X)

# 绘制降维后的数据点
plt.scatter(X_r[:, 0], X_r[:, 1], c=y)
plt.title("PCA of IRIS dataset")
plt.show()

通过本章的介绍，我们可以看到预测模型和数据挖掘技术在数据分析和处理中的重要性。下一章将探讨数理统计在特定领域中的数据分析应用。

以上是根据您的要求，对第四章内容的详细撰写。在此章节中，我们深入探讨了时间序列分析、分类与聚类分析以及关联规则和数据降维等关键主题，并通过代码、图表和示例来加深理解。在后续章节中，我们将继续探索数理统计在特定领域的应用。

# 5. 数理统计在特定领域的数据分析应用

## 5.1 金融数据分析

数理统计在金融领域扮演着至关重要的角色。金融分析师需要依靠数理统计来评估风险、优化投资策略、制定风险管理计划等。

### 5.1.1 风险评估与管理

风险评估是金融数据分析的核心环节。分析师通常使用各种统计模型来量化和管理风险。例如，Value at Risk (VaR) 模型是评估金融风险的一个常见工具，用于量化可能在正常市场条件下发生的最大潜在损失。

import numpy as np
import scipy.stats as scs

# 假设我们有一个投资组合的回报数据
returns = np.array([...])  # 一个包含投资组合日回报的数组

# 计算VaR
confidence_level = 0.95  # 置信水平
var = np.percentile(returns, (1 - confidence_level) * 100)
print(f"The {confidence_level*100}% VaR is {var:.2f}")

在上述代码中，我们使用了numpy和scipy来计算给定置信水平下的VaR值。

### 5.1.2 投资组合优化策略

投资组合优化是根据风险和回报之间的权衡来选择资产的组合。Markowitz模型是数理统计在这一领域应用的典范。该模型使用期望回报、方差和协方差来计算最优投资组合。

import pandas as pd
import cvxpy as cp

# 假设我们有资产的预期回报率和协方差矩阵
expected_returns = pd.Series([...])  # 预期回报率序列
cov_matrix = pd.DataFrame([...])  # 协方差矩阵

# 投资组合权重
weights = cp.Variable(len(expected_returns))
ret = expected_returns @ weights
risk = cp.quad_form(weights, cov_matrix)

# 目标是最大化预期回报同时最小化风险
objective = cp.Maximize(ret - 0.01 * risk)
constraints = [cp.sum(weights) == 1, weights >= 0]
prob = cp.Problem(objective, constraints)
prob.solve()

print(f"The optimal weights are {weights.value}")

在这个例子中，我们使用了cvxpy库来解决投资组合优化问题，通过约束投资组合总权重为1，并且权重非负，来找到最优权重。

## 5.2 生物统计学应用

生物统计学是应用统计方法来解决生物学和医学问题的一个分支。它在基因表达分析、临床试验设计、流行病学研究等方面有着广泛的应用。

### 5.2.1 基因表达数据分析

基因表达数据通常涉及高维数据集，生物统计学家使用数理统计方法来识别与特定疾病或条件相关的基因表达模式。

# 假设有一个基因表达矩阵
expression_matrix <- matrix([...], nrow=..., ncol=...)  # 表达矩阵

# 使用t检验识别差异表达的基因
group <- c(rep(0, 5), rep(1, 5))  # 假设有两组样本
t_test_result <- t.test(expression_matrix[,1], expression_matrix[,2], paired=FALSE)

print(t_test_result)

在R语言中，我们可以使用t.test函数来进行基因表达的差异分析。

### 5.2.2 流行病学研究中的应用

数理统计在流行病学中用于估计疾病的发病率、传播模式、以及预防措施的有效性等。

# 假设我们有关于某种疾病的病例数据和人口数据
cases <- c([...])  # 某疾病的病例数
population <- c([...])  # 相关人群的人口数

# 计算发病率
incidence_rate <- cases / population

# 使用泊松分布模型来模拟疾病的传播
pois_model <- glm(cases ~ population, family=poisson())
summary(pois_model)

在这个R代码块中，我们使用了广义线性模型（glm）来模拟疾病的流行情况。

## 5.3 社会科学研究中的应用

社会科学研究中常常需要处理大量复杂的数据集，使用数理统计方法可以更好地进行数据分析和结论推断。

### 5.3.1 调查数据分析与结论推断

调查数据分析经常使用抽样分布理论和假设检验来推断总体参数，并验证研究假设。

# 假设我们有某调查的样本数据
survey_data <- data.frame([...])  # 包含调查问题答案的DataFrame

# 进行均值的假设检验
sample_mean <- mean(survey_data$variable)  # 假设检验的样本均值
population_mean <- 0  # 假设的总体均值
n <- nrow(survey_data)  # 样本大小
std_dev <- sd(survey_data$variable)  # 样本标准差

# 计算t统计量和p值
t_statistic <- (sample_mean - population_mean) / (std_dev / sqrt(n))
p_value <- pt(t_statistic, df=n-1)

cat("T-statistic:", t_statistic, "\nP-value:", p_value)

在R中，我们通过计算t统计量和p值来进行均值的假设检验。

### 5.3.2 大数据时代下的统计学挑战与机遇

大数据时代对统计学带来了新的挑战和机遇。挑战包括数据质量和隐私保护问题，而机遇则体现在更精确的预测和个性化分析上。

graph TD
    A[大数据环境] -->|数据分析需求增长| B[统计学方法创新]
    B --> C[预测准确度提高]
    B --> D[个性化解决方案]
    A -->|隐私与质量| E[数据治理需求增加]
    E --> F[数据清洗与保护技术]

以上mermaid格式的流程图展示的是大数据环境对统计学的需求、挑战和创新的关系。

随着统计学与信息科学的不断融合，我们可以预见数理统计将会在特定领域中发挥更大的作用。通过上述的应用案例，我们可以看到，无论是在金融、生物还是社会研究领域，数理统计都提供了坚实的方法论基础，为决策提供科学依据。