PyTorch CNN图像分类深度研究：损失函数优化的关键决策


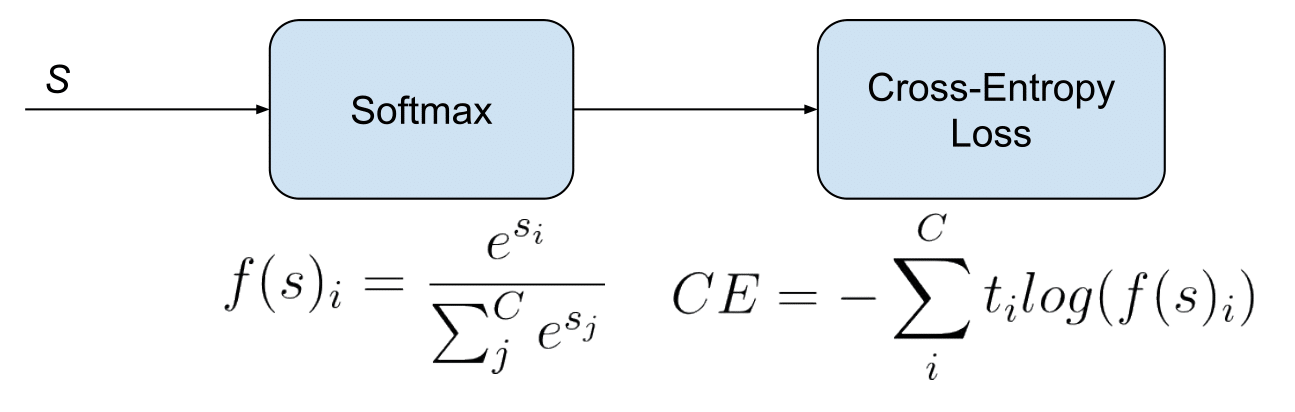
# 摘要
卷积神经网络（CNN）在图像分类任务中展现出了卓越的能力，而损失函数在其训练过程中扮演着核心角色。本文从损失函数的基础理论出发，详细阐述了损失函数的定义、作用和不同类型，特别是在CNN中的应用及对分类精度的影响。同时，文章深入探讨了损失函数的数学优化策略，包括梯度下降法、正则化和优化器选择，并提供了实际案例分析来说明从理论到实践的转化过程。此外，本文还展望了损失函数在未来深度学习领域的趋势，以及与注意力机制和模型蒸馏等技术的结合前景。

# 关键字
CNN；图像分类；损失函数；数学优化；梯度下降；模型性能

参考资源链接：[Pytorch CNN图像分类实战：4x4像素点内外部对比](https://wenku.csdn.net/doc/6401ad2ecce7214c316ee973?spm=1055.2635.3001.10343)
# 1. CNN图像分类概述

## 1.1 CNN的基本原理与应用
卷积神经网络（CNN）是深度学习领域中用于图像处理的一种强有力的模型，其设计灵感来源于生物的视觉感知机制。CNN通过模拟视觉皮层结构，实现了对图像的自动特征提取与学习，这使得它在图像分类、物体检测和图像分割等任务中取得了巨大的成功。

## 1.2 图像分类在CNN中的地位
图像分类是CNN应用中最为基础和经典的任务，它要求模型能够识别出图像中的主要物体，并将其归类到预定义的类别中。随着技术的发展，图像分类不仅仅局限于简单的分类，还包括了对图像中每个物体位置和类别的精确识别，即目标检测与实例分割。

## 1.3 CNN图像分类的挑战与进展
尽管CNN在图像分类方面取得了显著成就，但仍然面临诸多挑战，例如小样本学习、数据不平衡和类别泛化等。随着研究的深入，人们提出了各种策略和模型结构来克服这些困难，比如迁移学习、数据增强、生成对抗网络（GAN）等，这些进展持续推动CNN在图像分类领域的性能向更高水平迈进。

graph LR
A[图像输入] --> B[特征提取层]
B --> C[分类器]
C --> D[分类结果]

图1.1 CNN图像分类流程示意图

上图是一个简化的CNN图像分类流程图。模型接收输入图像，通过一系列卷积层和池化层提取特征，然后将这些特征送入分类器中，最终输出分类结果。在后续章节中，我们将深入探讨CNN如何利用损失函数提高分类的精度和效率。

# 2. 损失函数在CNN中的角色

## 2.1 损失函数的基本概念

### 2.1.1 损失函数定义及作用
损失函数（Loss Function）是机器学习中用于衡量模型预测值与真实值之间差异的函数。在监督学习任务中，损失函数的作用是提供一个评价标准，指导模型学习数据的内在规律。当模型预测值与实际值之间的差异最小化时，我们可以认为模型的性能最优。

在深度学习，尤其是卷积神经网络（CNN）中，损失函数是优化过程的关键，因为其反向传播算法直接依赖于损失函数的梯度信息。通过最小化损失函数，我们可以训练CNN来识别图像中的模式，并进行分类任务。

### 2.1.2 常见损失函数类型
在图像分类任务中，有几种常用的损失函数：
- **均方误差损失（MSE）**：常用于回归问题，通过计算预测值和真实值差值的平方来衡量损失。
- **交叉熵损失（Cross-Entropy Loss）**：更适合分类问题，尤其是多分类问题。它衡量的是预测概率分布与实际概率分布之间的差异。
- **对数损失（Log Loss）**：是交叉熵损失的另一个称呼，用于二分类问题。

在后续章节中，我们将详细介绍这些损失函数如何在CNN中应用，以及如何影响模型分类精度。

## 2.2 CNN中的损失函数

### 2.2.1 分类任务中常用的损失函数
在CNN的分类任务中，交叉熵损失函数是最为常用的。其数学表达式如下：

L = -∑(y_i * log(p_i) + (1 - y_i) * log(1 - p_i))

其中，`y_i` 表示实际的类别标签，而 `p_i` 表示模型预测的概率分布。使用交叉熵损失函数的原因是它为模型提供了一个更直接的梯度信息，这有助于在分类问题上加快收敛速度。

### 2.2.2 损失函数对分类精度的影响
损失函数的选取直接影响模型的分类精度。一个好的损失函数可以反映模型预测与真实标签的接近程度，且能通过梯度下降法有效地更新模型权重，以减少损失。如果损失函数选择不当，模型可能会过拟合或欠拟合，导致在新的数据上表现不佳。

## 2.3 选择合适的损失函数

### 2.3.1 损失函数的选择标准
选择合适的损失函数时，需要考虑问题的类型和任务的需求。例如，对于多分类问题，交叉熵损失通常是首选。对于二分类问题，通常使用对数损失。在有些情况下，如目标检测，可能需要使用不同的损失函数组合以达到最佳性能。

### 2.3.2 损失函数与模型性能的关系
模型性能不仅取决于损失函数的选择，还与损失函数的实现和调参有关。例如，学习率的选择、正则化项的添加，以及是否使用批归一化等，都会影响到损失函数的效果和模型的最终性能。在实际应用中，需要通过多次实验来找到最优的损失函数和模型配置。

在下一章中，我们将深入探讨损失函数的数学优化，以及如何在实践中通过不同的优化策略来提高模型的性能。

# 3. 损失函数的数学优化

在第三章中，我们将深入探讨损失函数背后的数学原理及其优化策略。通过本章的学习，读者将能够理解损失函数在数学上的定义，如何使用梯度下降法进行优化，以及在实践中如何应用各种技术来解决优化过程中可能遇到的问题。

## 3.1 损失函数的数学基础

### 3.1.1 导数和梯度的概念

在数学优化中，导数和梯度是两个核心概念。导数可以被看作是函数在某一点上斜率的量度，表示函数