MATLAB图像二值化：从理论到实践，全面掌握二值化图像处理技术

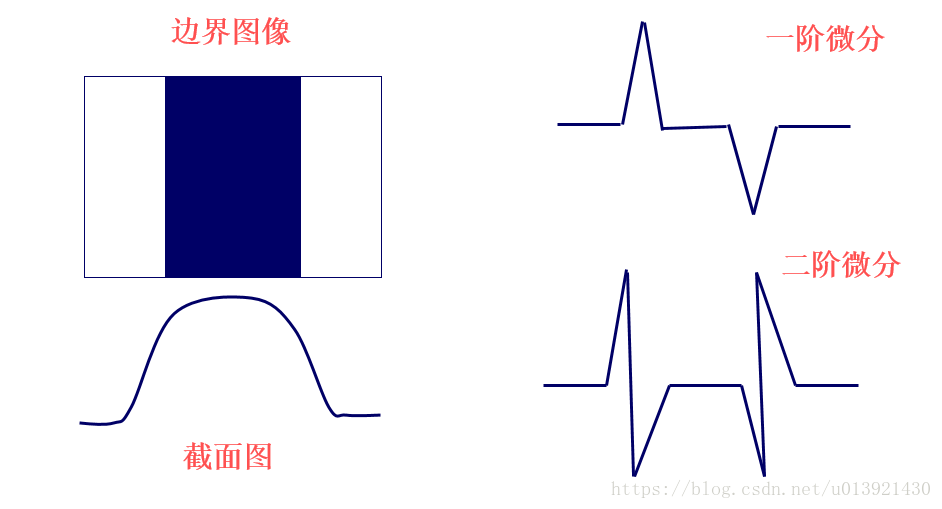
# 1. 图像二值化的理论基础**

图像二值化是将灰度图像转换为二值图像的过程，其中像素值仅为 0（黑色）或 1（白色）。其理论基础在于图像灰度分布的分析。

灰度分布直方图可以描述图像中不同灰度值的分布情况。对于二值图像，直方图通常呈现双峰分布，其中两个峰值对应于背景和目标区域。通过选择适当的阈值，可以将图像分割为这两个区域。

阈值选择是图像二值化的关键步骤。常用的阈值选择方法包括固定阈值法和自适应阈值法。固定阈值法使用全局阈值将图像二值化，而自适应阈值法根据图像局部特性动态调整阈值。

# 2. MATLAB图像二值化方法

图像二值化是将灰度图像转换为二值图像的过程，其中像素值仅为0（黑色）或1（白色）。MATLAB提供了多种图像二值化方法，可根据图像的特性和应用要求进行选择。

### 2.1 基于阈值的二值化

基于阈值的二值化通过比较每个像素值与阈值来确定像素的二值化结果。

#### 2.1.1 固定阈值法

固定阈值法使用一个预定义的阈值来二值化图像。如果像素值大于或等于阈值，则将其设置为1（白色）；否则，将其设置为0（黑色）。

% 读取图像
image = imread('image.jpg');

% 设定阈值
threshold = 128;

% 二值化图像
binaryImage = image > threshold;

#### 2.1.2 自适应阈值法

自适应阈值法根据图像的局部信息动态调整阈值。它适用于图像具有不均匀照明或对比度变化的情况。

% 读取图像
image = imread('image.jpg');

% 使用自适应阈值法二值化图像
binaryImage = imbinarize(image, 'adaptive');

### 2.2 基于区域的二值化

基于区域的二值化将图像分割成不同的区域，然后根据区域的属性（如面积、形状）进行二值化。

#### 2.2.1 连通域分析

连通域分析将图像中相邻的具有相同像素值的像素分组为连通域。然后，可以根据连通域的面积或其他属性进行二值化。

% 读取图像
image = imread('image.jpg');

% 进行连通域分析
connectedComponents = bwconncomp(image);

% 根据连通域面积进行二值化
binaryImage = bwareaopen(connectedComponents, 100);

#### 2.2.2 分水岭算法

分水岭算法将图像视为地形图，其中像素值代表高度。算法从图像中的最大值开始，并逐渐向周围的低值区域扩展，直到遇到分水岭（即两个相邻区域之间的边界）。

% 读取图像
image = imread('image.jpg');

% 使用分水岭算法二值化图像
binaryImage = watershed(image);

# 3. MATLAB图像二值化实践

### 3.1 图像读取和预处理

在进行图像二值化之前，需要先读取图像并进行必要的预处理。MATLAB提供了`imread`函数读取图像，并将其存储为矩阵。

% 读取图像
image = imread('image.jpg');

图像预处理通常包括灰度转换、噪声去除和图像增强等步骤。

% 灰度转换
grayImage = rgb2gray(image);

% 噪声去除
denoisedImage = medfilt2(grayImage);

% 图像增强
enhancedImage = imadjust(denoisedImage);

### 3.2 基于阈值的二值化实现

基于阈值的二值化是将图像像素值与阈值进行比较，高于阈值的像素设置为白色（1），低于阈值的像素设置为黑色（0）。

% 固定阈值法
threshold = 128;
binaryImage = grayImage > threshold;

% 自适应阈值法
binaryImage = imbinarize(grayImage, 'adaptive');

### 3.3 基于区域的二值化实现

基于区域的二值化将图像分割成不同的区域，然后根据区域的特征（如面积、形状）进行二值化。

#### 3.3.1 连通域分析

连通域分析将图像中的相邻像素分组为连通域。

% 连通域分析
[labeledImage, numObjects] = bwlabel(binaryImage);

#### 3.3.2 分水岭算法

分水岭算法将图像视