MATLAB信号处理算法：从基础到应用，深入理解信号处理，解决现实问题

# 1. 信号处理基础

信号处理是一门处理和分析信号（表示物理量随时间或空间变化的函数）的学科。它在许多领域都有着广泛的应用，如通信、图像处理、语音处理和生物医学。

信号处理的基础知识包括：

- **信号分类：**连续信号和离散信号、确定信号和随机信号。
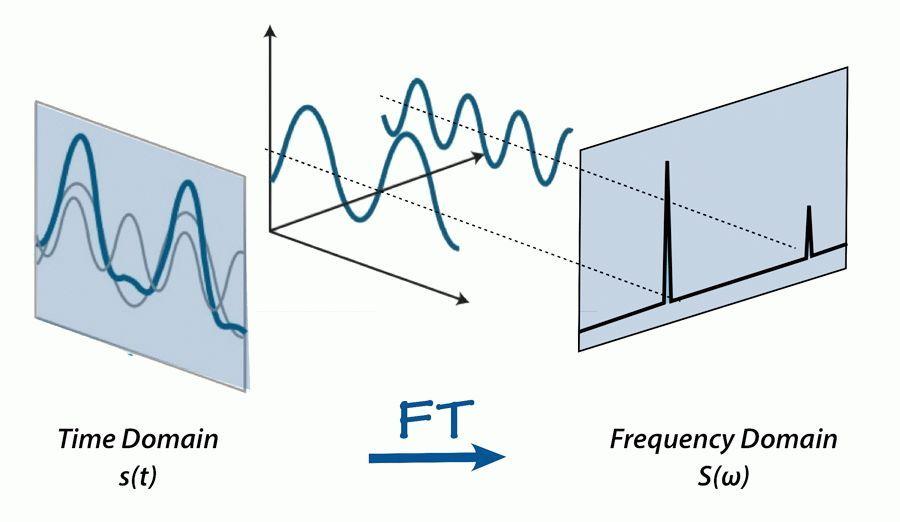
- **信号表示：**时域和频域表示。
- **信号变换：**傅里叶变换、拉普拉斯变换等，用于将信号从时域转换为频域或其他域。

# 2. 信号处理算法理论**

**2.1 时域分析**

时域分析是指在时间域内对信号进行分析。它主要用于研究信号的时变特性，如信号的幅度、频率和相位随时间的变化。

**2.1.1 傅里叶变换**

傅里叶变换是时域信号与频域信号之间的桥梁。它将时域信号分解为一系列正弦波和余弦波的叠加，每个正弦波或余弦波对应于一个特定的频率。

import numpy as np
import matplotlib.pyplot as plt

# 定义一个时域信号
t = np.linspace(0, 1, 1000)
x = np.sin(2 * np.pi * 10 * t) + np.cos(2 * np.pi * 20 * t)

# 进行傅里叶变换
X = np.fft.fft(x)

# 计算频率
f = np.fft.fftfreq(len(x), d=t[1] - t[0])

# 绘制时域和频域信号
plt.subplot(2, 1, 1)
plt.plot(t, x)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Time Domain Signal')

plt.subplot(2, 1, 2)
plt.plot(f, np.abs(X))
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.title('Frequency Domain Signal')
plt.show()

**参数说明：**

* `fft.fft()`：执行傅里叶变换
* `fftfreq()`：计算频率

**代码逻辑分析：**

* 傅里叶变换将时域信号分解为一系列正弦波和余弦波。
* 频率对应于正弦波或余弦波的振荡周期。
* 频域信号的幅度表示每个频率分量的强度。

**2.1.2 拉普拉斯变换**

拉普拉斯变换是傅里叶变换的推广，它将时域信号映射到复频域。拉普拉斯变换可以用于分析信号的稳定性、因果关系和响应特性。

from scipy import signal

# 定义一个时域信号
t = np.linspace(0, 1, 1000)
x = np.exp(-2 * t) * np.sin(2 * np.pi * 10 * t)

# 进行拉普拉斯变换
X = signal.laplace(x, t)

# 绘制时域和复频域信号
plt.subplot(2, 1, 1)
plt.plot(t, x)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Time Domain Signal')

plt.subplot(2, 1, 2)
plt.plot(X.real, X.imag)
plt.xlabel('Real Frequency')
plt.ylabel('Imaginary Frequency')
plt.title('Complex Frequency Domain Signal')
plt.show()

**参数说明：**

* `signal.laplace()`：执行拉普拉斯变换

**代码逻辑分析：**

* 拉普拉斯变换将时域信号映射到复频域。
* 复频域信号的实部和虚部分别表示信号的稳定性和因果关系。
* 拉普拉斯变换可以用于分析信号的极点和零点，这些极点和零点对应于信号的谐振和衰减特性。

**2.2 频域分析**

频域分析是指在频率域内对信号进行分析。它主要用于研究信号的频率特性，如信号的频谱分布、带宽和谐振频率。

**2.2.1 频谱分析**

频谱分析是频域分析中最常用的技术。它将信号分解为一系列频率分量，并显示每个频率分量的幅度和相位。

# 使用傅里叶变换进行频谱分析
X = np.fft.fft(x)
f = np.fft.fftfreq(len(x), d=t[1] - t[0])

# 绘制频谱
plt.plot(f, np.abs(X))
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.title('Spectrum')
plt.show()

**2.2.2 滤波器设计**

滤波器设计是频域分析的另一个重要应用。滤波器可以用来滤除信号中的特定频率分量，从而实现信号的增强、降噪或其他处理目的。

# 设计一个低通滤波器
order = 5
cutoff_freq = 10
b, a = signal.butter(order, cutoff_freq, btype='low')

# 应用滤波器
y = signal.filtfilt(b, a, x)

# 绘制原始信号和滤波后信号
plt.subplot(2, 1, 1)
plt.plot(t, x)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Original Signal')

plt.subplot(2, 1, 2)
plt.plot(t, y)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Filtered Signal')
plt.show()

**参数说明：**

* `signal.butter()`：设计巴特沃斯滤波器
* `filtfilt()`：应用滤波器

**代码逻辑分析：**

* 巴特沃斯滤波器是一种经典的模拟滤波器，它具有平坦的通带和陡峭的截止特性。
* `filtfilt()`函数可以应用滤波器，同时消除相移失真。

# 3. MATLAB信号处理算法实践

### 3.1 信号生成和可视化

#### 3.1.1 信号生成函数

MATLAB提供了多种信号生成函数，可用于创建各种类型的信号，包括正弦波、方波、三角波和噪声。常用的信号生成函数包括：

- `sin()`：生成正弦波
- `square()`：生成方波
- `sawtooth()`：生成三角波