MATLAB矩阵求逆的子空间分析：揭示矩阵求逆的几何意义，深入理解求逆本质

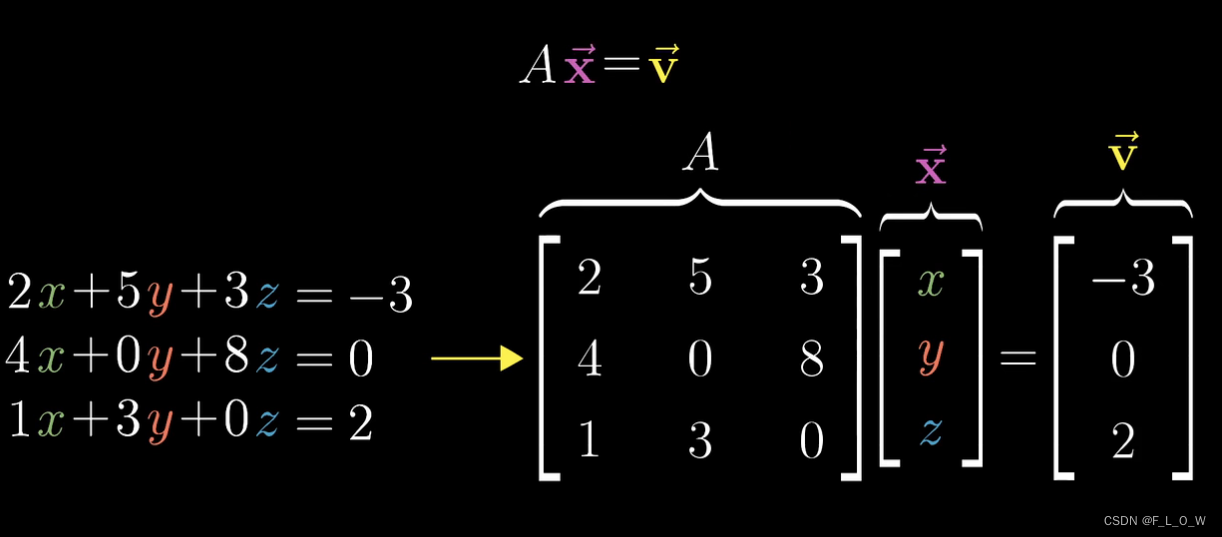
# 1. MATLAB矩阵求逆的基本概念和理论

矩阵求逆是线性代数中的一项基本操作，它求解一个矩阵的逆矩阵，即另一个矩阵，当与原矩阵相乘时得到单位矩阵。在MATLAB中，矩阵求逆可以通过`inv()`函数实现。

矩阵的逆矩阵存在的前提是矩阵为非奇异矩阵，即矩阵的行列式不为零。对于奇异矩阵，不存在逆矩阵。矩阵的行列式可以通过`det()`函数计算。

逆矩阵具有以下性质：

- 对于非奇异矩阵A，其逆矩阵A^-1唯一存在。
- (AB)^-1 = B^-1A^-1
- (A^-1)^-1 = A

# 2.1 矩阵的秩和行列空间

**矩阵的秩**

矩阵的秩是指其线性无关的行或列的最大数量。秩可以表示为矩阵中非零奇异值的数量。

**行列空间**

矩阵的行列空间是由其行向量张成的线性子空间。它表示矩阵可以表示的所有线性组合。行列空间的维度等于矩阵的秩。

**计算矩阵的秩**

使用MATLAB计算矩阵的秩：

A = [1 2 3; 4 5 6; 7 8 9];
rank(A)

**代码逻辑分析：**

* `rank()` 函数计算矩阵的秩。
* 结果为 3，表示矩阵的秩为 3，即矩阵有 3 个线性无关的行。

**参数说明：**

* `A`：输入矩阵

**行列空间的几何意义**

行列空间是一个几何对象，可以可视化为矩阵行向量张成的超平面。矩阵的秩等于行列空间的维度，表示超平面的维数。

**例如：**

考虑矩阵 A：

A = [1 2 3; 4 5 6]

* A 的秩为 2，因为只有前两行是线性无关的。
* A 的行列空间是一个二维超平面，由向量 [1, 2, 3] 和 [4, 5, 6] 张成。

# 3.1 使用MATLAB求解矩阵的秩

**秩的定义**

矩阵的秩表示矩阵中线性无关的行或列的最大数量。秩可以用来确定矩阵是否可逆，以及求解矩阵的零空间和行列空间。

**MATLAB中求解秩**

MATLAB中使用`rank()`函数求解矩阵的秩。该函数返回一个标量，表示矩阵的秩。

% 定义矩阵 A
A = [1 2 3; 4 5 6; 7 8 9];

% 求解矩阵 A 的秩
rank_A = rank(A);

% 打印秩
disp(['秩为：' num2str(rank_A)]);

**示例：**

考虑矩阵 A：

A = [1 2 3; 4 5 6; 7 8 9];

使用`rank()`函数求解矩阵 A 的秩：

rank_A = rank(A);

输出：

秩为：3

因此，矩阵 A 的秩为 3，表示矩阵 A 中有 3 个线性无关的行或列。

**逻辑分析：**

`rank()`函数通过以下步骤求解矩阵的秩：

1. 将矩阵转换为行阶梯形。
2. 计算行阶梯形中非零行的数量。
3. 非零行的数量