MATLAB复数优化算法：利用复数优化算法解决实际问题，高效求解

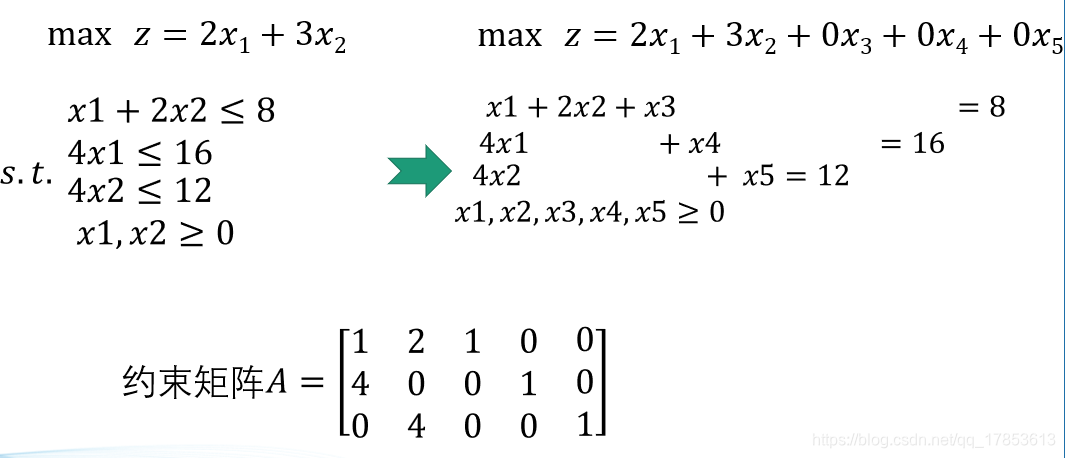
# 1. 复数优化算法概述**

复数优化算法是一种利用复数域的特性来解决优化问题的算法。与传统的实数优化算法相比，复数优化算法具有以下优势：

- **探索能力强：**复数域的维度比实数域高，这使得复数优化算法能够更有效地探索搜索空间。
- **收敛速度快：**复数优化算法利用复数域的旋转和镜像对称性，可以更快地收敛到最优解。

# 2.1 复数数域及其运算

### 2.1.1 复数数域

复数域，记作 C，是一个包含所有形式为 a + bi 的数的集合，其中 a 和 b 是实数，i 是虚数单位，满足 i^2 = -1。

复数可以表示为一个有序对 (a, b)，其中 a 是实部，b 是虚部。复数也可以用极坐标表示为 r(cosθ + isinθ)，其中 r 是模长，θ 是辐角。

### 2.1.2 复数运算

复数的运算与实数类似，但由于虚数单位的存在，复数运算具有一些独特的性质。

**加法和减法：**

(a + bi) + (c + di) = (a + c) + (b + d)i
(a + bi) - (c + di) = (a - c) + (b - d)i

**乘法和除法：**

(a + bi) * (c + di) = (ac - bd) + (ad + bc)i
(a + bi) / (c + di) = ((ac + bd) + (bc - ad)i) / (c^2 + d^2)

**共轭：**
复数的共轭，记作 z*，定义为 z* = a - bi。

**模长：**
复数的模长，记作 |z|，定义为 |z| = sqrt(a^2 + b^2)。

**辐角：**
复数的辐角，记作 arg(z)，定义为 arg(z) = arctan(b/a)。

# 3.1 复数粒子群优化算法（CPSO）

#### 3.1.1 CPSO 的原理和实现

复数粒子群优化算法（CPSO）是一种基于粒子群优化算法（PSO）的复数优化算法。PSO 是一种群体智能算法，其灵感来自于鸟群或鱼群等自然界中的集体行为。在 CPSO 中，每个粒子代表一个潜在的解决方案，并具有位置和速度。粒子根据自身经验和群体经验更新其位置和速度，从而搜索最优解。

CPSO 与 PSO 的主要区别在于，CPSO 在复数域中进行操作。复数域是一个包含复数的集合，复数由实部和虚部组成。复数域中的运算与实数域中的运算类似，但具有额外的特性，例如共轭和模。

CPSO 的实现如下：

1. **初始化粒子群：**随机初始化一组粒子，每个粒子具有一个复数位置和一个复数速度。
2. **评估粒子：**计算每个粒子的适应度值，这反映了粒子对优化问题的解决方案的优劣程度。
3. **更新粒子：**根据粒子自身的最佳位置（pBest）和群体最佳位置（gBest）更新每个粒子的速度和位置。更新公式如下：

v_i(t+1) = w * v_i(t) + c1 * r1 * (pBest_i - x_i(t)) + c2 * r2 * (gBest - x_i(t))
x_i(t+1) = x_i(t) + v_i(t+1)

其中：

* `v_i(t)` 是粒子 `i` 在时间 `t` 的速度。
* `x_i(t)` 是粒子 `i` 在时间 `t` 的位置。
* `pBest_i` 是粒子 `i` 的最佳位置。
* `gBest` 是群体最佳位置。
* `w` 是惯性权重，控制粒子的探索和利用能力。
* `c1` 和 `c2` 是学习因子，控制粒子向 pBest 和 gBest 移动的程度。
* `r1` 和 `r2` 是 [0, 1] 范围内的随机数。

4. **重复步骤 2-3：**重复评估