图像质量评估：SSIM原理深度解析及其在现代处理中的不可替代性


参考资源链接：[水下图像质量评估：UCIQE、UIQM与关键指标解析](https://wenku.csdn.net/doc/36v1jj2vck?spm=1055.2635.3001.10343)
# 1. 图像质量评估与SSIM的必要性

## 1.1 图像质量评估的重要性
在当今的数字时代，图像的质量评估至关重要。它广泛应用于多媒体传输、医学影像分析、安防监控等多个领域。图像质量评估可以指导图像处理算法的优化，保证最终用户获得满意的视觉体验。

## 1.2 传统图像质量评估方法的局限性
传统的图像质量评估方法如峰值信噪比（PSNR）依赖于像素间的均方误差，但其并不能很好地模拟人类视觉系统（HVS）对图像质量的主观感受。因此，寻找一种能更好反映人类视觉体验的评估方法成为必要。

## 1.3 结构相似性原理
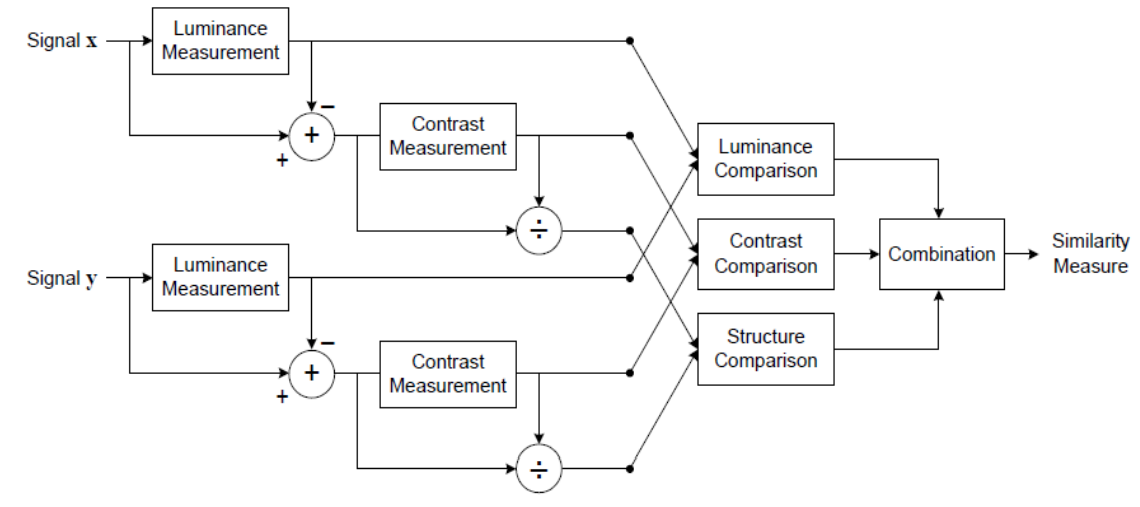
为了克服传统方法的局限性，结构相似性（SSIM）算法应运而生。SSIM基于图像局部区域亮度、对比度和结构信息的相似性进行评估，从而更贴近人类视觉感知特性。通过这种方式，SSIM提供了一种更全面和准确的图像质量评价标准。

# 2. SSIM算法原理

## 2.1 图像质量评估的重要性

### 2.1.1 传统图像质量评估方法的局限性
在数字图像处理领域，图像质量评估(IQA)是一个核心议题。传统的图像质量评估方法主要分为三类：主观评估、全参考评估和无参考评估。

主观评估依赖于人类观察者的反馈，评价结果主观性较强，不具有普适性，且费时费力。全参考评估方法，如均方误差(MSE)和峰值信噪比(PSNR)，要求比较图像与参考图像完全相同，这在实际应用中往往难以实现。无参考评估方法，虽然在不依赖于参考图像方面具有优势，但往往精度较低，很难真实反映图像质量。

这些方法普遍存在的问题是对人类视觉感知理解的不足，不能准确模拟人眼对图像质量的感知，导致评估结果与人类主观感受存在较大偏差。

### 2.1.2 人类视觉系统的模拟与重要性
为了提高评估的准确性，研究者开始尝试模拟人类视觉系统(HVS)。人类视觉系统对图像的感知依赖于亮度、对比度、颜色和边缘信息的综合处理。因此，基于结构相似性的图像质量评估方法(Structural Similarity Index Measurement, SSIM)应运而生，致力于更贴近人眼对图像质量的感知。

SSIM算法在评估时，通过比较图像中局部结构、亮度和对比度的相似度，提供了一种在视觉上更为合理的质量评估方式。SSIM算法的出现，弥补了传统评估方法的不足，为图像质量的精确评估提供了新思路。

## 2.2 SSIM算法的理论基础

### 2.2.1 结构相似性原理
SSIM算法的核心是结构相似性原理，该原理认为图像质量可以通过比较图像的局部结构信息来评估。人眼对图像中的一些局部结构信息非常敏感，如边缘、角点等。这些局部结构信息在视觉感知中起着重要作用。

SSIM的计算原理是假设一幅图像由多个局部区域构成，每个区域中图像的结构信息是相似的。如果一幅图像在经过某种处理后，其局部区域内的结构信息仍然保持高度相似性，则认为该图像的质量较高。

### 2.2.2 SSIM数学模型与公式解析
SSIM的数学模型主要基于三个主要因素：亮度、对比度和结构。这三者共同构成了衡量图像质量的标准。SSIM数学模型的计算公式如下：

\[ SSIM(x, y) = \frac{(2\mu_x\mu_y + c_1)(2\sigma_{xy} + c_2)}{(\mu_x^2 + \mu_y^2 + c_1)(\sigma_x^2 + \sigma_y^2 + c_2)} \]

其中，\(x\) 和 \(y\) 分别代表原始图像和待评估图像中的局部窗口，\(\mu_x\) 和 \(\mu_y\) 是局部窗口的均值，\(\sigma_x^2\) 和 \(\sigma_y^2\) 是局部窗口的方差，\(\sigma_{xy}\) 是两个窗口的协方差，\(c_1\) 和 \(c_2\) 是防止分母为零的小常数。

该公式通过比较两个图像窗口的均值、方差和协方差来评估图像局部区域的结构相似性，从而判断图像质量。

## 2.3 SSIM与PSNR等其他指标的对比

### 2.3.1 PSNR的原理及其缺陷
PSNR（峰值信噪比）是广泛使用的图像质量评估指标之一，其定义基于均方误差（MSE）。PSNR的计算公式如下：

\[ PSNR = 20 \cdot \log_{10}(MAX_I) - 10 \cdot \log_{10}(MSE) \]

其中，\(MAX_I\) 是图像中像素值的最大可能亮度，\(MSE\) 是原始图像和处理后图像之间的均方误差。

尽管PSNR在很多情况下被用作图像质量的客观标准，但它存在一些明显的缺陷。比如，它无法充分反映人眼的视觉特性，对图像内容的依赖性较强，并且对图像的亮度和对比度变化不够敏感。

### 2.3.2 SSIM在图像质量评估中的优势
与PSNR相比，SSIM更接近人类的主观感受。SSIM在评估时考虑了图像的结构信息、亮度信息以及对比度信息，这些都直接关联到人类的视觉感知。因此，SSIM能够更好地评估图像质量，尤其是对图像压缩、图像去噪等处理过程后图像质量的评估。

由于SSIM评估的是局部图像的结构相似性，因此它对于图像的一些细节，如边缘、纹理等变化更为敏感，能够较准确地反映出图像质量的变化。这使得SSIM成为研究者和工程师在图像处理领域中的一个重要工具。

接下来的章节，我们将深入探讨SSIM算法的实践应用，并展示如何在实际场景中使用和优化SSIM以评估和提升图像质量。

# 3. SSIM算法的实践应用

## 3.1 SSIM算法的实现细节

### 3.1.1 常用编程语言下的SSIM实现

结构相似性指数（SSIM）算法是一种广泛应用于图像处理领域，尤其是在图像质量评估中的技术。它模拟了人类视觉系统对图像结构信息的感知能力，通过比较图像的亮度、对比度和结构信息来评估图像的相似度。下面以Python语言为例，介绍如何实现SSIM算法。

在Python中，我们可以使用`skimage`库中的`structural_similarity`函数来计算两张图像之间的SSIM值。这个函数简单易用，但对于想要深入理解SSIM算法的用户来说，通过手动实现SSIM算法，可以更好地掌握其核心思想和实现细节。

首先，我们需要准备两张图像，通常是一张参考图像和一张待评估的图像。然后，计算这两张图像的均值、标准差和协方差。SSIM计算公式如下：

\[ SSIM(x, y) = \frac{(2\mu_x\mu_y + C_1)(2\sigma_{xy} + C_2)}{(\mu_x^2 + \mu_y^2 + C_1)(\sigma_x^2 + \sigma_y^2 + C_2)} \]

其中，\( \mu_x \) 和 \( \mu_y \) 分别是两幅图像的均值，\( \sigma_x^2 \) 和 \( \sigma_y^2 \) 分别是它们的方差，\( \sigma_{xy} \) 是两幅图像的协方差，\( C_1 \) 和 \( C_2 \) 是避免分母为零的常数项。

以下是一个简单的SSIM算法的Python代码示例：

import numpy as np
from skimage.metrics import structural_similarity as ssim

def calculate_ssim(img1, img2):
    # 计算均值
    mu1 = np.mean(img1)
    mu2 = np.mean(img2)
    # 计算方差
    sigma1 = np.var(img1)
    sigma2 = np.var(img2)
    # 计算协方差
    sigma12 = np.cov(img1.flatten(), img2.flatten())[0][1]

    ssim_value = (2 * mu1 * mu2 + 0.001) / (mu1 ** 2 + mu2 ** 2 + 0.001)
    ssim_value *= (2 * sigma12 + 0.001) / (sigma1 + sigma2 + 0.001)
    return ssim_value

### 3.1.2 实现过程中参数调整与优化

在实现SSIM算法时，参数调整是一个重要的优化环节。常见的参数包括窗口大小（用于局部计算SSIM时的邻域大小）、\( C_1 \) 和 \( C_2 \) 的具体数值。这些参数对于算法的结果会产生显著影响，因此合理选择这些参数至关重要。

- **窗口大小**：通过改变窗口大小，可以控制算法对局部细节的敏感程度。较大的窗口可以获得更多的结构信息，但可能会掩盖细节；较小的窗口对细节敏感，但容易受到噪声的影响。
- **\( C_1 \) 和 \( C_2 \)**：这两个常数项用于防止分母为零的情况。它们的选择依赖于图像数据类型和应用场景。\( C_1 \) 和 \( C_2 \) 常用值为 \( (K_1L)^2 \) 和 \( (K_2L)^2 \)，其中 \( L \) 是像素值的动态范围，\( K_1 \) 一般取0.01，\( K_2 \) 一般取0.03。

在实际应用中，用户可以通过实验来确