波函数与量子计算:量子比特和量子算法,解锁量子计算的无限潜力
发布时间: 2024-07-11 23:36:16 阅读量: 59 订阅数: 31 

# 1. 量子计算的理论基础
量子计算是一种利用量子力学原理进行计算的新兴技术。其理论基础建立在量子力学的基本概念之上,包括量子叠加、量子纠缠和量子态。
### 量子叠加
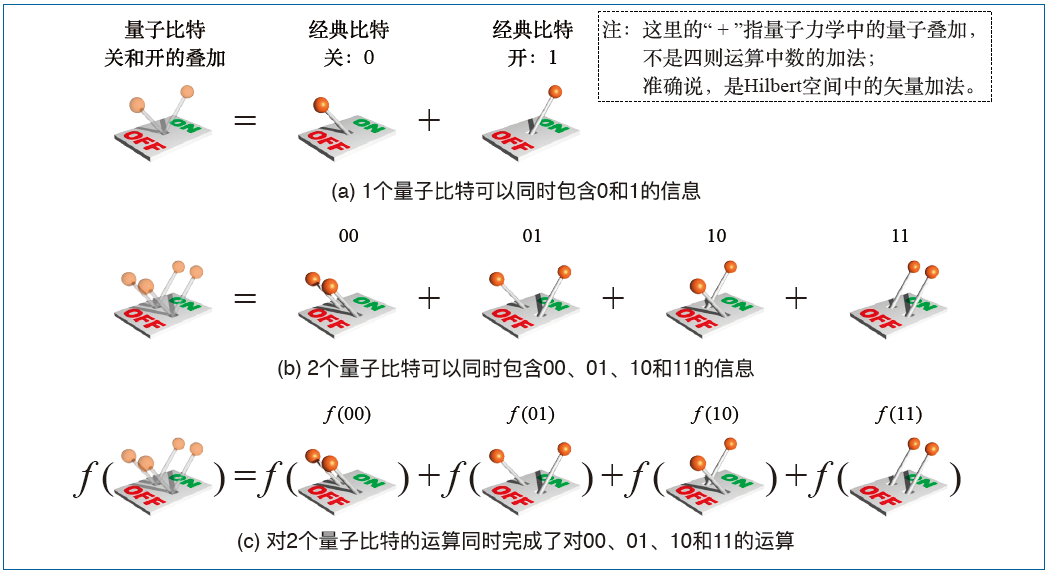
量子叠加是量子力学中一个重要的概念,它允许一个量子系统同时处于多个状态。例如,一个量子比特(量子信息的最小单位)可以同时处于 0 和 1 的状态,称为叠加态。
### 量子纠缠
量子纠缠是另一个关键的概念,它描述了两个或多个量子系统之间的一种非局部相关性。当两个量子系统纠缠时,它们的行为不再是独立的,即使它们被物理地分开。
# 2. 量子比特与量子态
### 2.1 量子比特的定义和特性
#### 2.1.1 量子叠加态
量子比特(Qubit)是量子计算的基本单位,与经典比特不同,量子比特可以处于叠加态,即同时处于 0 和 1 的状态。这种叠加态可以用狄拉克表示法表示为:
```
|\psi⟩ = α|0⟩ + β|1⟩
```
其中,α 和 β 是复数,满足 |α|² + |β|² = 1。α² 表示量子比特处于 |0⟩ 状态的概率,β² 表示量子比特处于 |1⟩ 状态的概率。
#### 2.1.2 量子纠缠
量子纠缠是一种量子现象,其中两个或多个量子比特相互关联,以至于它们的状态不能独立描述。纠缠的量子比特的行为与经典比特完全不同。例如,两个纠缠的量子比特可以同时处于 00、01、10 和 11 的叠加态。
### 2.2 量子态的表示和操作
#### 2.2.1 量子态的狄拉克表示法
量子态可以用狄拉克表示法表示为一个复数向量,其中向量的每个元素对应于量子比特的可能状态。例如,一个量子比特的量子态可以表示为:
```
|\psi⟩ =
```
#### 2.2.2 量子态的幺正变换
幺正变换是一种保持量子态归一化的线性变换。幺正变换可以用来操作量子态,例如:
```
U|\psi⟩ = |\psi'⟩
```
其中,U 是幺正矩阵,|\psi⟩ 是初始量子态,|\psi'⟩ 是变换后的量子态。
# 3. 量子算法与量子电路
### 3.1 量子算法的基本原理
#### 3.1.1 量子并行性和干涉
量子算法与经典算法的一个主要区别在于量子并行性。经典算法一次只能处理一个输入,而量子算法可以同时处理多个输入。这是因为量子比特可以处于叠加态,即同时处于 0 和 1 的状态。
量子干涉是量子算法的另一个重要特性。当多个量子比特处于叠加态时,它们可以相互干涉,产生比经典算法更强大的计算能力。例如,Grover 算法使用量子干涉来搜索无序数据库,其时间复杂度为 O(√N),而经典算法的时间复杂度为 O(N)。
#### 3.1.2 量子纠错和容错
量子计算面临的一个主要挑战是量子比特的脆弱性。量子比特容易受到噪声和干扰的影响,这可能导致计算错误。为了解决这个问题,量子算法使用了纠错机制。
量子纠错码是一种数学技术,用于检测和纠正量子比特中的错误。通过使用纠错码,我们可以将量子计算的容错能力提高到可以实际应用的水平。
### 3.2 量子电路的构建和执行
#### 3.2.1 量子门和量子操作
量子电路是由量子门和量子操作组成的。量子门是作用于量子比特的酉算子,可以改变量子比特的状态。常见的量子门包括 Hadamard 门、CNOT 门和 Toffoli 门。
量子操作是作用于量子电路的更一般的操作,可以包括量子门、测量和条件操作。量子操作可以用来构建更复杂的量子算法。
#### 3.2.2 量子电路的优化和编译
量子电路的优化和编译对于提高量子算法的性能至关重要。优化可以减少量子电路中量子门的数量,而编译可以将量子电路转换为特定量子计算机的机器代码。
量子电路优化技术包括门合并、电路分解和冗余消除。量子电路编译技术包括量子汇编和量子仿真。
```python
# 量子电路优化示例:门合并
circuit = QuantumCircuit(2)
circuit.h(0)
circuit.cx(0, 1)
circuit.h(0)
circuit = circuit.optimize() # 优化电
```
0
0





