【优化算法】多目标蝗虫优化算法（MOGOA）.md

摘要

本文首先概述了动态多目标优化问题的基本概念，然后重点介绍了MOGOA算法的理论基础、实践应用以及在实际问题中的应用。在理论基础部分，文章详细阐述了多目标优化问题的定义、常见方法以及MOGOA算法的结构框架和关键操作步骤。此外，针对动态环境下的适应性进行了探讨，分析了MOGOA在模拟动态特性下的响应机制。在实践应用章节，本文通过动态多目标测试函数进行算法的实验设计与评估，比较了MOGOA在动态环境中的表现和性能优势，并提供了资源分配和网络优化中的实际应用案例。最后，文章展望了MOGOA算法的未来研究方向和挑战，包括算法的改进方向和动态多目标优化的未来趋势。

关键字

动态多目标优化；MOGOA算法；算法实践应用；资源分配；网络优化；未来研究方向

参考资源链接：多目标优化：蝗虫优化算法（MOGOA）解析

1. 动态多目标优化问题概述

1.1 问题定义

在多目标优化领域中，动态多目标优化问题（DMOOP）是近年来备受关注的研究方向。动态环境的变化是其核心特征，这使得优化问题在求解过程中会遇到一系列的挑战，如目标函数、约束条件的突变等。这些变化要求优化算法不仅要具备高效的问题求解能力，还必须具备良好的适应性和稳定性。

1.2 动态环境下的挑战

动态多目标优化问题的挑战主要体现在三个方面：

环境动态变化：目标函数、约束条件或参数可能在优化过程中发生变化，要求算法能够及时响应并调整策略。
多目标权衡：解决多个目标之间的冲突，寻求最佳权衡解，即Pareto最优解集。
效率与质量的权衡：在保证解的多样性与覆盖度的同时，提升算法的搜索效率和解的质量。

动态多目标优化问题为研究者提供了广阔的研究空间，促进了智能算法在处理实际问题时的性能提升。接下来的章节将对MOGOA算法进行详细探讨，展示其在解决动态多目标问题中的优势和应用案例。

2. MOGOA算法理论基础

2.1 多目标优化问题基础

2.1.1 多目标优化问题定义

多目标优化问题是指在给定的一个或多个目标函数的情况下，同时寻找一个解集合，这个解集合能使得这些目标函数的值同时达到最优。对于每一个目标，我们希望得到的是最佳可能值，但是通常这些目标是相互冲突的，无法同时实现最优。因此，多目标优化问题的解通常是一组权衡不同目标的解集合，被称为Pareto最优解集合。

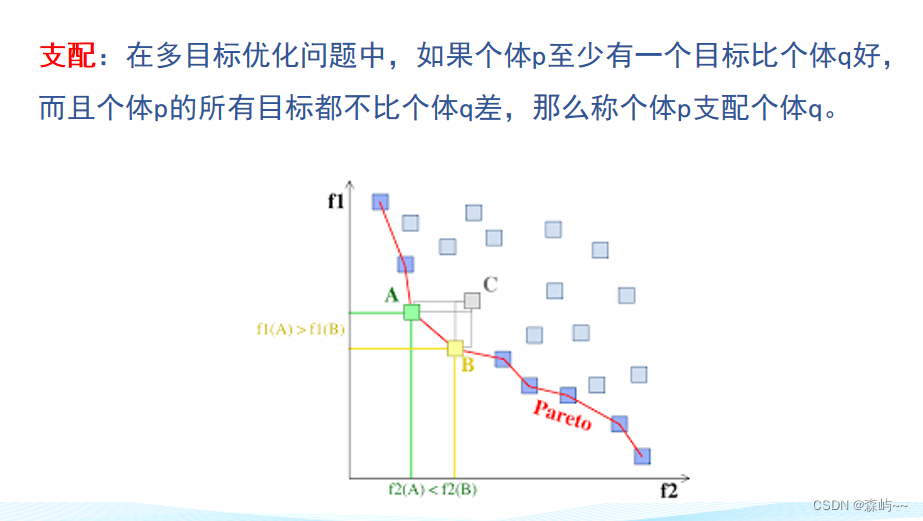
解的支配关系是多目标优化领域中的一个核心概念。如果在所有考虑的目标上，一个解都至少和另一个解一样好，且在至少一个目标上比另一个解更好，那么我们说这个解支配了另一个解。Pareto最优解集合就是由那些不被任何其他解支配的解组成的集合。

2.1.2 常见的多目标优化方法

在多目标优化领域，已经发展出多种方法，包括但不限于：

权重法：通过给不同的目标设置不同的权重，将多目标问题转化为单目标问题。但这种方法的缺点是难以提前知道每个目标的相对重要性。
ε-约束法：固定某些目标，将它们转化为约束条件，只优化其他目标。这种方法在目标数量较多时，决策空间可能会变得非常复杂。
Pareto前沿方法：直接寻找Pareto最优解集合，而不需事先设定目标权重或转化问题形式。其中，进化算法在这一方法中应用广泛。

2.2 MOGOA算法原理

2.2.1 MOGOA算法结构框架

MOGOA（Multi-objective Genetic Optimization Algorithm）算法，是一种基于遗传算法的多目标优化算法。它采用生物进化的概念，通过模拟自然选择和遗传机制对潜在解决方案进行优化。MOGOA的核心是种群进化，种群中的每个个体代表了解空间中的一个候选解。

MOGOA算法的结构框架主要包括以下几个步骤：

初始化：随机生成一组解作为初始种群。
适应度评估：计算种群中每个个体的适应度值，通常这些值基于要优化的目标函数。
选择：根据个体的适应度值，选择一部分优秀的个体进行繁殖。
交叉与变异：在选中的个体上执行交叉和变异操作，生成新的个体。
更新：用新生成的个体替换当前种群中的某些个体，形成新的种群。
终止条件：检查算法是否达到终止条件，如达到了设定的迭代次数或解的质量已足够好。

2.2.2 算法的关键操作和步骤

在MOGOA算法中，关键操作包括选择、交叉和变异。这些操作直接影响算法的搜索能力和最终解的质量。

选择操作：用来模仿自然界中的“适者生存”。在MOGOA中，常用的选择方法有轮盘赌选择、锦标赛选择等。这些方法都倾向于选择那些适应度高的个体进行繁殖。
交叉操作：也称为杂交或重组，是指将两个或多个个体的部分基因组合起来形成新的个体。在多目标优化中，交叉操作的目的是为了产生能够更好地覆盖Pareto前沿的新个体。
变异操作：是指随机改变个体的某些基因，以增加种群的多样性。在MOGOA中，常用的变异操作包括位变异、均匀变异等。

2.3 动态环境下的算法适应性

2.3.1 动态环境的特性与挑战

在动态环境下，目标函数和/或约束条件会随时间变化。这种变化可以是连续的，也可以是不连续的；可能是缓慢的，也可能是快速的；可能是周期性的，也可能是完全随机的。动态环境带来的挑战包括：

解的稳定性：解在环境变化后是否仍然有效。
解的适应性：算法能否快速适应环境的变化并找到新的最优解。
计算资源：算法需要在有限的时间和计算资源内对环境变化做出响应。

2.3.2 MOGOA对动态变化的响应机制

MOGOA针对动态环境引入了特殊的响应机制。这些机制包括：

种群多样性维持：定期通过变异操作引入新的基因，保持种群多样性，以应对环境的变化。
环境变化检测：算法周期性地评估环境是否发生了变化，一旦检测到变化，触发特定的应对策略。
策略调整：针对不同的动态变化类型，设计不同的策略，如增加变异率、调整选择压力、引入记忆机制等。

通过这些机制，MOGOA能够较好地适应动态变化的环境，并持续提供高质量的解。

最低0.47元/天解锁专栏

买1年送3月

点击查看下一篇

百万级高质量VIP文章无限畅学

千万级优质资源任意下载

C知道免费提问 ( 生成式Al产品 )

【动态环境适应】：MOGOA在动态多目标问题上的应用分析

摘要

关键字

1. 动态多目标优化问题概述

1.1 问题定义

1.2 动态环境下的挑战

2. MOGOA算法理论基础