微分学的精妙：Apostol数学分析中的微分技术深度探讨


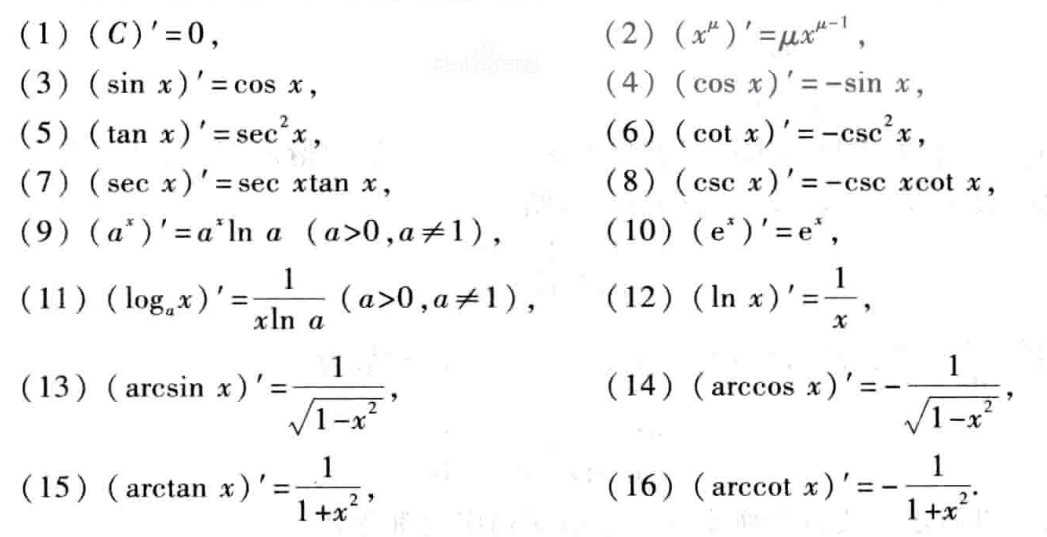
# 摘要
微分学作为数学分析的核心部分，它构建了现代数学和应用科学的根基。本文旨在系统性地回顾微分学的基础概念、极限与连续性理论、微分的计算及其在不同学科中的应用。深入探讨了隐函数、参数方程以及多元函数微分学的相关原理，并对Apostol所提出的微分学方法论进行了详细介绍。本文还展望了微分学在现代数学领域中的角色，并预测了微分技术在未来新兴学科中的应用前景及数学分析研究的发展趋势。

# 关键字
微分学；极限理论；连续函数；微分技术；多元函数；数学分析

参考资源链接：[Tom Apostol Mathematical Analysis 2ed.pdf](https://wenku.csdn.net/doc/646b3bb35928463033e70d2f?spm=1055.2635.3001.10343)
# 1. 微分学的根基与概念

## 导入微分学的定义
微分学，作为数学分析的核心部分，围绕变量的局部变化率和无限小增量展开。它的基础概念包括导数和微分，是研究函数局部性质的重要工具。对IT行业的高级从业者来说，微分学不仅在算法设计和系统优化中有着实际应用，而且在理解更高级数学概念，如机器学习中的梯度下降法时，也扮演了重要的角色。

## 微分学的基本原理
导数的定义是微分学的基石。直观上，它表示函数在某一点处的瞬时变化率。更精确地说，给定函数f(x)，其在点a的导数，如果存在，表示为f'(a)，定义为
\[ f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} \]
当这个极限存在时，我们称函数在该点可导。可导性隐含了函数在该点的连续性，尽管反之不一定成立。

## 微分学的意义
微分学的深层意义在于，它不仅仅是一系列计算技巧的集合，更是一种分析和理解连续变化过程的思维方式。对于任何领域的从业者而言，掌握微分学的基本原理，可以帮助他们更好地分析问题，预测系统行为，并且设计出更加高效和精确的解决方案。例如，在处理非线性问题，或是在研究计算机图形学中的曲面插值时，微分学的应用就显得尤为重要。

# 2. 微分学中的极限与连续性

### 2.1 极限理论的基本原理

极限是微分学中一个核心概念，它描述了一个函数在接近某一点时的趋势和行为。理解极限理论对于深入掌握微分学至关重要。

#### 2.1.1 极限的定义与性质

极限的直观理解是指当自变量趋近于某一点时，函数值接近某个固定的值。在数学上，对于函数 f(x)，当 x 趋近于 c 时，如果存在一个常数 L，使得 f(x) 可以任意接近 L，那么我们称 L 为函数在 c 点的极限，记作 lim_{x→c} f(x) = L。

极限具有以下性质：
- 唯一性：如果极限存在，则唯一。
- 局部有界性：如果函数在某一点的极限存在，那么在这一点的邻域内，函数有界。
- 保号性：如果极限大于（小于）零，则在该点的某邻域内，函数值同样大于（小于）零。
- 保序性：如果 a < b，则在它们的极限存在时，lim f(x) < lim g(x)。

#### 2.1.2 无穷小与无穷大

无穷小是指当 x 趋近于某个值时，函数值趋近于 0 的量。无穷小的性质是它在数量级上可以忽略不计。

无穷大则是当 x 趋近于某点时，函数值的绝对值可以无限增大。例如，1/x 当 x 趋近于 0 时，函数值会无限增大，所以 1/x 是无穷大。

### 2.2 连续函数的分析

连续函数是微分学中的另一个基础概念。一个函数在某一点连续，意味着当自变量趋近于这一点时，函数值的变化是平滑的，没有突变。

#### 2.2.1 连续性的判定方法

函数在点 c 连续的判定条件包括：
1. 在 c 点有定义。
2. 在 c 点有极限。
3. 函数在 c 点的极限值等于函数值，即 lim_{x→c} f(x) = f(c)。

如果函数在区间内每一点都连续，那么我们称这个函数在该区间上连续。

#### 2.2.2 间断点的分类与应用

间断点是函数连续性的中断点。间断点可以分为三种类型：
1. 可去间断点：极限存在，但函数值可能不存在。
2. 跳跃间断点：左极限和右极限存在但不相等。
3. 无穷间断点：函数在某点的绝对值无限大。

了解间断点的分类有助于分析函数的性质，以及在实际应用中对函数行为的预测。

### 2.3 极限过程中的微分技术

极限过程中的微分技术是微分学中的一个高级主题，涉及到极限运算与微分法则的结合使用，以及多重极限与偏导数的求解。

#### 2.3.1 极限运算与微分法则

极限运算遵循一系列法则，包括和差积商的极限运算法则。微分法则如乘积法则和链式法则允许我们求复合函数的导数，这对于复杂函数极限的计算至关重要。

举个例子，如果函数 f(x) 和 g(x) 在 c 点连续，那么它们的和 f(x) + g(x) 在 c 点也连续。类似地，乘积 f(x) * g(x) 和商 f(x)/g(x)（g(x) 不为零）在 c 点也连续，前提是它们在 c 点的极限存在。

#### 2.3.2 多重极限与偏导数

多重极限指的是考虑多个自变量的极限情况。偏导数是函数在某一点沿坐标轴方向的瞬时变化率。计算多重极限和偏导数能够揭示函数在多维空间中的局部行为。

在求解多变量函数的偏导数时，例如 f(x, y)，首先固定 x，对 y 求导，然后固定 y，对 x 求导，可以得到函数沿 x 和 y 方向的变化率。

import sympy as sp

# 定义变量
x, y = sp.symbols('x y')

# 定义函数
f = x**2 + 3*x*y + y**2

# 计算偏导数
df_dx = sp.diff(f, x)  # 对 x 求偏导
df_dy = sp.diff(f, y)  # 对 y 求偏导

print("偏导数 ∂f/∂x =", df_dx)
print("偏导数 ∂f/∂y =", df_dy)

输出结果将会是：

偏导数 ∂f/∂x = 2*x + 3*y
偏导数 ∂f/∂y = 3*x + 2*y

通过使用符号计算库（如 Python 的 sympy），我们可以直观地计算并验证这些偏导数的表达式，从而深入理解函数在不同方向上的变化趋势。

# 3. 微分的计算与应用

微分的计算是微分学中的核心内容之一，是分析变量间关系变化率的基础。本章将深入探讨导数与微分的计算方法，演示如何将这些概念应用于实际问题中，并介绍微分方程的基本概念及求解策略。

## 3.1 导数与微分的计算方法

导数是微分学中的基础概念，其反映了函数在某一点处的瞬时变化率。微分则提供了在该点附近函数值变化的线性近似。

### 3.1.1 基本导数表

掌握一组基本