【泛化能力】：因变量与模型泛化能力的关系研究

# 1. 泛化能力的基本概念和重要性

## 1.1 泛化能力的基本概念

在机器学习和统计学领域，泛化能力是指一个模型对于未知数据的预测能力。它衡量的是一个模型在新样本上的表现如何，而不是仅仅在训练数据集上进行拟合。一个具有强泛化能力的模型能够在面对未曾见过的数据时，做出准确预测或分类。

## 1.2 泛化能力的重要性

泛化能力是评估模型效能的关键指标之一。模型若仅在训练集上表现良好而无法推广到新数据，则称为过拟合。过拟合意味着模型丧失了泛化能力，无法对现实世界中的数据作出准确反应。因此，研究和提升模型的泛化能力，对于构建实用和高效的机器学习系统至关重要。

## 1.3 泛化能力的衡量与实践意义

衡量泛化能力通常通过测试集上的误差来评估，使用诸如均方误差、交叉验证等方法。在实践中，确保模型具有良好的泛化能力意味着需要在模型设计、数据处理、训练过程等多方面进行细致考虑。泛化能力的提高，意味着模型的鲁棒性和可靠性增强，这对推动机器学习技术的实际应用尤为重要。

# 2. 泛化能力的理论基础

## 2.1 泛化能力的定义和度量

### 2.1.1 泛化能力的定义

泛化能力是指一个学习算法在未知数据上的性能。一个具有高泛化能力的算法能够从有限的训练样本中提取出有效的信息，从而对新样本做出准确的预测或决策。换言之，泛化能力描述了模型对未见过数据的预测能力，这是衡量学习算法优劣的重要指标。

在机器学习领域，泛化能力反映了模型对数据内在规律的理解程度。这种能力使得模型不仅能够在已有的数据集上表现良好，而且能够应对新的、未参与训练的输入数据。高泛化能力的模型在现实世界的应用中更为重要，因为现实世界的环境往往比训练环境更为复杂和多变。

### 2.1.2 泛化能力的度量方法

度量泛化能力的常见方法有如下几种：

- **留出法（Hold-out method）**：将数据集分为训练集和测试集，训练模型在训练集上学习，然后在测试集上评估泛化误差。这是一种简单而有效的方法，但存在随机性，不同的数据划分可能导致结果的不同。

- **交叉验证法（Cross-validation method）**：例如k-折交叉验证，将数据集分为k个大小相似的互斥子集。每次使用k-1个子集进行训练，剩余的一个子集用来评估模型性能，重复k次，每次选择不同的子集作为测试集。这种方法能够减小数据划分带来的随机性影响，并能更充分地利用有限的数据。

- **学习曲线（Learning curve）**：通过绘制训练误差和验证误差随样本量增加而变化的曲线，可以直观地观察模型在不同样本量下的泛化能力。

在实际操作中，通常会结合多种方法来全面评估模型的泛化能力，以确保评估的准确性和可靠性。

## 2.2 泛化能力的影响因素

### 2.2.1 数据集特性的影响

数据集的特性会直接影响模型的泛化能力，主要包括以下方面：

- **数据质量**：数据的准确性和完整性是关键。噪声和异常值会误导模型学习错误的特征，降低模型泛化能力。
- **数据多样性**：数据应覆盖到问题的各个方面，具有足够的多样性，以确保模型能够学习到泛化规律。
- **数据量**：足够的训练样本有助于模型更好地捕捉数据的分布特征。但样本量过多可能导致过拟合，即模型在训练集上性能优异，但泛化能力差。

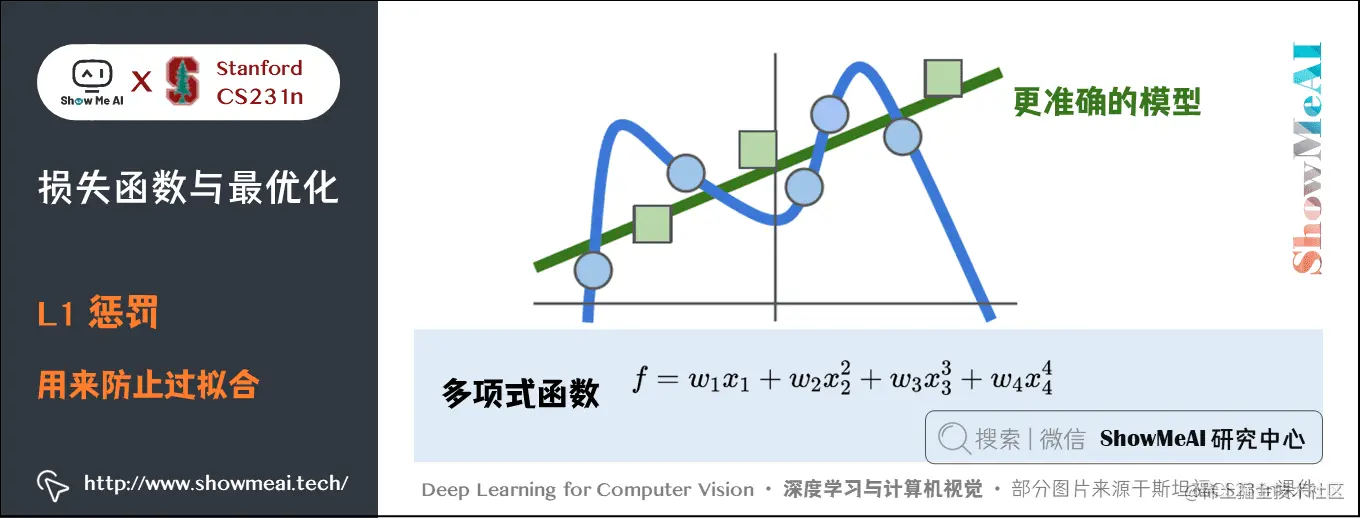
### 2.2.2 模型复杂度的影响

模型复杂度与泛化能力的关系遵循偏差-方差权衡原则：

- **模型复杂度过低**：容易导致欠拟合（high bias），模型不能充分捕捉数据的内在规律。
- **模型复杂度过高**：容易导致过拟合（high variance），模型过度学习训练集的噪声和特定细节，缺乏泛化性。

因此，选择合适的模型复杂度是提高泛化能力的重要环节。复杂度需要根据具体问题和数据特性进行调整，通常通过模型选择和正则化技术来实现。

### 2.2.3 训练算法的影响

训练算法对泛化能力的影响主要体现在优化过程和收敛速度上：

- **优化算法**：选择合适的优化算法以更快地收敛到最优解，同时避免局部最优和过拟合的问题。
- **早期停止（Early Stopping）**：在训练过程中监视验证误差，并在验证误差开始增加时停止训练，以避免过拟合。
- **正则化技术**：在损失函数中增加惩罚项，使得模型更加平滑，倾向于学习简单的、泛化能力强的决策边界。

## 2.3 泛化能力的理论模型

### 2.3.1 VC维理论

VC维（Vapnik–Chervonenkis Dimension）是描述学习算法能力的一个概念。简单来说，VC维度越高，模型能表示的类别组合就越复杂。VC维理论提供了一种量化模型复杂度的方法，并给出了泛化误差的上界估计，即模型在新样本上犯错的概率不会超过某个阈值。

### 2.3.2 PAC学习理论

PAC（Probably Approximately Correct）学习理论是一种概率框架，用来分析学习算法在给定一定样本量下，产生正确模型的概率。PAC理论为学习过程的可实现性和效率提供了理论保证。

### 2.3.3 经验风险最小化与结构风险最小化

经验风险最小化（Empirical Risk Minimization, ERM）的目标是使训练误差最小化，但如果模型复杂度过高，则可能导致过拟合。

结构风险最小化（Structural Risk Minimization, SRM）则通过引入正则化项（惩罚项），在经验风险的基础上，同时控制模型复杂度，试图达到更好的泛化效果。

结构风险最小化方法通过平衡模型的复杂度和经验风险，从而避免过拟合并提高模型的泛化能力。

# 3. 泛化能力与因变量关系的研究方法

## 3.1 因变量的选择和特征分析

### 3.1.1 因变量的定义和选择依据

因变量，也被称作响应变量或目标变量，在统计学与机器学习中扮演着重要角色，它是研究者希望预测或解释的变量。定义一个清晰的因变量是进行有效研究的关键步骤之一。选择因变量的依据通常包括研究问题的性质、数据的可用性、预期的模型复杂性以及最终预测或分类任务的目标。

在选择因变量时，研究者需要确保所选变量能够充分反映问题的实质，并具有足够的解释力。例如，在医学研究中，因变量可能是疾病的发生与否；在金融分析中，可能是股票价格的涨跌；在营销研究中，则可能是消费者的购买决策。

### 3.1.2 因变量的特征分析方法

一旦确定了因变量，接下来的步骤是对因变量进行深入的特征分析。特征分析帮助我们了解变量的分布特性、取值范围、潜在的异常值以及与其他变量的相关性等。常见的特征分析方法包括：

- **描述性统计分析**：计算因变量的均值、中位数、标准差、偏度、峰度等统计指标，以了解其分布特征。
- **数据可视化**：利用箱线图、直方图、散点图等图形工具直观地展示因变量的分布情况。
- **异常值检测**：通过标准差、四分位数距离等方法识别可能的异常值，并决定是否进行处理。
- **相关性分析**：检验因变量与自变量之间是否存在统计意义上的相关性，常用的方法包括皮尔逊相关系数、斯皮尔曼秩相关系数等。

通过这些方法，研究者可以为后续的泛化能力分析打下坚实的基础。

## 3.2 泛化能力与因变量关系的统计分析

### 3.2.1 相关性分析

在探讨泛化能力与因变量的关系时，相关性分析是基础。它帮助我们理解两者之间的相关程度和方向。统计学中，相关系数是衡量变量间相关性的重要工具，其中皮尔逊相关系数是最常用的一种。

假设我们有因变量 \( Y \) 和自变量 \( X \)，皮尔逊相关系数 \( r \) 的计算公式如下：

r = \frac{\sum_{i=1}^{n}(X_i - \bar{X})(Y_i - \bar{Y})}{\sqrt{\sum_{i=1}^{n}(X_i -