【响应面分析最佳实践】：软件测试中不可或缺的8大技巧和经验


# 摘要
响应面分析是一种统计学方法，用于确定影响过程或产品性能的关键因素。本文首先概述了响应面分析的基本概念和目的，并详细介绍了响应面分析理论基础中的关键术语、模型类型。接着，本文阐述了响应面分析的实施步骤，包括实验设计、数据收集与分析、模型的建立与验证。在此基础上，文章探讨了响应面分析在软件测试中的实践应用，着重分析了提升测试效率、性能测试优化以及自动化测试的策略。最后，本文深入讨论了响应面分析的高级技巧与经验进阶拓展，并对未来的趋势进行了展望，强调了与人工智能和机器学习结合的潜力。

# 关键字
响应面分析；理论基础；实验设计；数据分析；性能测试；软件测试

参考资源链接：[Design-Expert响应面设计教程：BBD实操详解与分析](https://wenku.csdn.net/doc/1fmx465u22?spm=1055.2635.3001.10343)
# 1. 响应面分析概述

在现代IT领域，特别是在工程和科学试验设计中，响应面分析是一种用来研究一个或多个响应变量如何受一组影响因素或输入变量影响的统计技术。它通过建立一个统计模型，描绘输入变量与响应变量之间的关系，从而达到预测和优化研究目标的目的。

响应面分析不仅可以帮助我们理解变量之间的复杂相互作用，还能指导我们如何调整输入变量以获得期望的输出响应。它在减少实验次数、理解交互效应、优化产品和过程设计等方面发挥着重要作用。

随着数据分析工具和软件的不断进步，响应面分析已经从传统的制造业拓展到了软件工程、生物技术、环境科学等多个领域。在接下来的章节中，我们将深入探讨响应面分析的理论基础，实施步骤，以及在软件测试中的实践应用，帮助读者全面掌握这项技术。

# 2. 响应面分析的理论基础

### 2.1 响应面分析的定义和目的

#### 2.1.1 响应面分析的概念

响应面分析（Response Surface Methodology, RSM）是一种统计学上的方法，用于研究一个或多个响应变量与一组影响因素之间的关系。RSM通过数学模型的建立，来近似这些关系，进而通过模型进行优化和预测。它的核心思想是利用实验设计来拟合一个近似函数，这个函数可以用来描述响应变量随着输入参数变化的趋势，并在数学上构建一个或多个响应变量和影响因素之间的关系。

在实际应用中，响应面分析不仅可以帮助我们理解变量间的关系，还可以基于已知条件预测变量在新条件下的可能结果。在工程、医药、化学、食品工业、软件工程等领域都有广泛应用。

#### 2.1.2 分析的目的和意义

响应面分析的主要目的是：

- **确定最佳操作条件**：通过分析，找出影响因素对响应值的最佳水平组合。
- **预测和优化**：在已知的操作范围内，对响应值进行预测，并尝试优化这些响应值。
- **减少实验次数**：通过优化的实验设计和数学模型，减少实验次数，节省实验成本。
- **理解变量间的关系**：通过模型拟合，理解自变量与因变量之间的相互作用。

从更深层次的意义上讲，响应面分析是解决问题的一种系统化方法，能够揭示输入与输出之间的复杂关系，并提供决策支持。在工程实践中，这种方法可以帮助工程师和研究人员在不确定性中找到清晰的决策路径，减少因猜测或直觉导致的失误。

### 2.2 响应面方法的关键术语

#### 2.2.1 因变量与自变量

在响应面分析中，因变量（Response Variables）是指受一个或多个自变量（Independent Variables）影响的输出值。自变量通常是可以通过实验或操作进行控制的输入参数，因变量则是在实验或研究过程中观察和测量的输出指标。

例如，在软件性能测试中，我们可以将系统的响应时间作为因变量，而自变量可能是并发用户数、服务器负载、网络延迟等。了解和区分这些变量对于建立准确的模型至关重要。

#### 2.2.2 响应值和影响因素

响应值（Response Values）是因变量在不同实验条件下的测量值。而影响因素（Influencing Factors）是指可能会影响响应值的所有变量。在统计学中，这些影响因素又被称为解释变量或预测变量。

响应面分析的目的是建立响应值与影响因素之间的函数关系，这个函数关系可以通过实验数据进行拟合。通过拟合出的函数，我们可以在自变量变化时预测响应值的变化趋势，进而进行优化。

### 2.3 常见的响应面模型类型

#### 2.3.1 线性模型

线性模型是最简单的响应面模型类型，它假设因变量与自变量之间的关系可以通过一条直线来描述。虽然在实际应用中，这种模型并不常见，因为它不能捕捉大多数现象中的非线性特征，但在某些情况下，如果变量间的关系确实近似线性，该模型可以提供快速且有效的结果。

线性模型的数学表达形式通常为：

Y = β_0 + Σ(β_iX_i) + ε

其中，`Y` 表示响应值，`X_i` 表示自变量，`β_0` 是截距项，`β_i` 是模型系数，`ε` 是误差项。

#### 2.3.2 非线性模型

大多数情况下，变量之间的关系更为复杂，非线性模型因此被广泛使用。在非线性模型中，因变量与自变量之间的关系被假定为曲线关系，可以是二次曲线、多项式曲线或其他形式的曲线。

一个简单的非线性模型示例是二次模型：

Y = β_0 + Σ(β_iX_i) + Σ(β_ijX_iX_j) + ε

在此模型中，除了线性项外，还包括了变量之间的交互项（`X_iX_j`）和平方项（`X_i^2`）。

#### 2.3.3 交互模型

交互模型关注于自变量之间的相互作用对响应值的影响。在多变量分析中，了解变量间的相互作用至关重要，因为单独的变量可能不会对结果有显著影响，但它们的组合却可能产生显著的效果。

交互模型的一般形式可以表示为：

Y = β_0 + Σ(β_iX_i) + Σ(β_ijX_iX_j) + ε

这里，`β_ijX_iX_j`代表了自变量`X_i`和`X_j`之间的交互项，它允许模型捕捉变量间复杂的关系。

以上介绍了响应面分析的基本概念、关键术语以及常见的模型类型。为了深入理解这些模型在实际中的应用，下一章节将详细介绍响应面分析的实施步骤。我们将从实验设计开始，逐步深入到数据收集和分析，最后介绍如何建立和验证响应面模型。

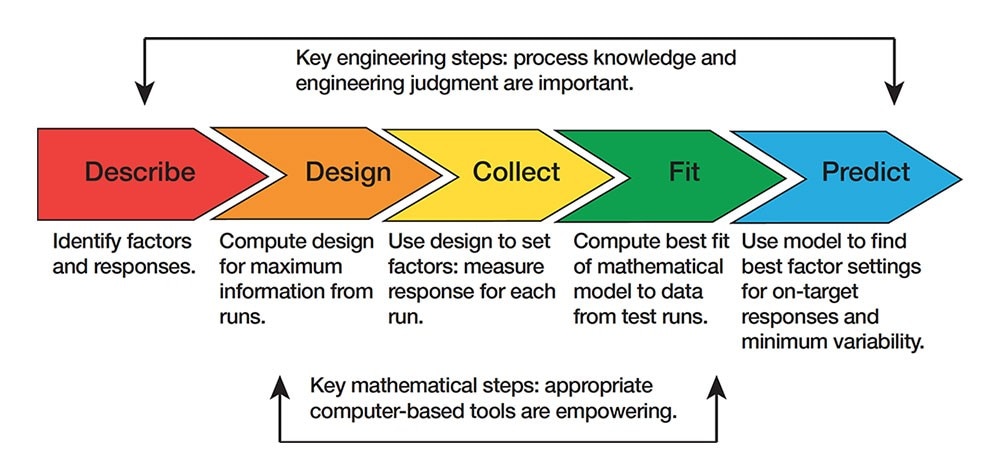
# 3. 响应面分析的实施步骤

## 3.1 实验设计阶段

### 3.1.1 选择合适的实验设计

实验设计是响应面分析中的一个关键步骤，它决定了后续实验的效率和结果的可靠性。在选择实验设计时，需要考虑实验的目标、可用资源以及时间限制。常见的实验设计类型包括全因子设计、分式因子设计以及中心复合设计等。全因子设计提供了所有变量所有水平的组合