Python代码数据结构与算法：高效解决复杂问题，提升代码效率

# 1. 数据结构基础**

数据结构是组织和存储数据的有效方式，是算法的基础。它定义了数据的存储方式以及访问和修改数据的操作。常见的数据结构包括数组、链表、栈、队列、树和图。

数据结构的选择取决于算法的需求。例如，数组适合存储顺序数据，而链表适合存储动态数据。栈和队列遵循先进先出（FIFO）和后进先出（LIFO）原则，用于管理任务或消息。树和图用于表示层次结构或网络。

# 2. 算法设计与分析

### 2.1 算法的基本概念

算法是解决特定问题的一系列明确的指令。它描述了将输入转换为输出的步骤。算法的质量由其效率、正确性和可读性来衡量。

**算法的特性：**

- **输入：** 算法接收的一组初始值。
- **输出：** 算法产生的结果。
- **明确性：** 算法的每一步都必须明确定义，没有歧义。
- **有限性：** 算法必须在有限的时间内终止。
- **有效性：** 算法必须产生正确的输出。

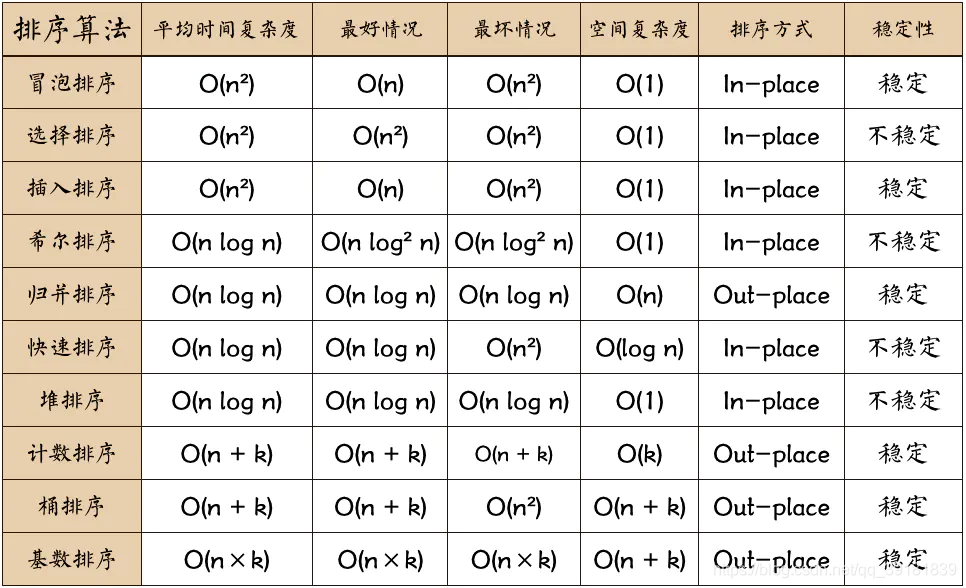
### 2.2 算法复杂度分析

算法复杂度分析衡量算法在不同输入规模下的运行效率。它主要分为时间复杂度和空间复杂度。

#### 2.2.1 时间复杂度

时间复杂度表示算法执行所需的时间。通常使用大 O 符号表示，表示算法在输入规模 n 趋于无穷大时的渐进行为。

**常见的时间复杂度：**

- O(1)：常数时间，与输入规模无关。
- O(log n)：对数时间，随着输入规模的增加，执行时间以对数方式增长。
- O(n)：线性时间，执行时间与输入规模成正比。
- O(n^2)：平方时间，执行时间与输入规模的平方成正比。
- O(2^n)：指数时间，执行时间随着输入规模的增加呈指数增长。

#### 2.2.2 空间复杂度

空间复杂度表示算法执行所需的内存空间。它也使用大 O 符号表示，表示算法在输入规模 n 趋于无穷大时的渐进空间占用。

**常见的空间复杂度：**

- O(1)：常数空间，与输入规模无关。
- O(n)：线性空间，空间占用与输入规模成正比。
- O(n^2)：平方空间，空间占用与输入规模的平方成正比。

**代码示例：**

# 计算斐波那契数列的第 n 项
def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

**复杂度分析：**

* 时间复杂度：O(2^n)，因为算法递归调用自身，每个调用都会将输入规模减小 1。
* 空间复杂度：O(n)，因为算法使用递归调用栈，其深度与输入规模成正比。

# 3.1 数组与链表

#### 数组

数组是一种线性数据结构，其中元素存储在连续的内存位置中。数组中的每个元素都具有一个唯一的索引，该索引用于访问该元素。数组的主要优点是快速访问元素，因为我们可以直接使用索引来获取元素。

**代码示例：**

# 创建一个数组
my_array = [1, 2, 3, 4, 5]

# 访问数组中的元素
print(my_array[2])  # 输出：3

**逻辑分析：**

* `my_array`是一个数组，其中包含5个元素。
* `my_array[2]`访问数组中索引为2的元素，该元素的值为3。

#### 链表

链表是一种线性数据结构，其中元素存储在不连续的内存位置中。每个元素包含数据和指向下一个元素的指针。链表的主要优点是插入和删除元素的效率很高，因为不需要移动其他元素。

**代码示例：**

# 创建一个链表节点
clas