初识PCA主成分分析：如何理解主成分及其应用

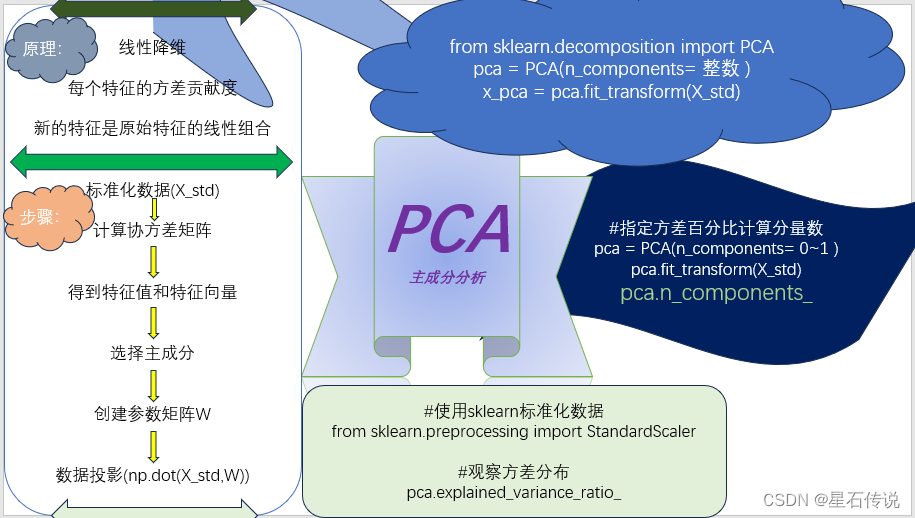
# 1. 介绍PCA主成分分析

主成分分析（PCA）是一种常用的数据降维技术，通过线性变换将原始数据映射到一个新的特征空间，使得数据在新空间中的各主成分方向上的方差最大化。PCA可以用于降低数据的维度同时保留最重要的信息，从而便于可视化和模式识别等应用。主成分分析背后的数学原理涉及到协方差矩阵、特征值与特征向量等概念，通过对特征向量的选择可以实现数据的降维和特征提取。在实际应用中，PCA被广泛应用于图像处理、金融数据分析等领域，为数据分析和机器学习提供了有效的工具和方法。

希望以上内容可以帮助您更好地了解PCA主成分分析的基本概念和应用场景，为后续深入学习和实践奠定基础。

# 2. PCA主成分分析的数学基础

### 2.1 主成分分析中的数据预处理
在主成分分析中，数据的预处理是至关重要的一步，主要包括数据的标准化及中心化处理。
#### 2.1.1 数据标准化及中心化处理
数据标准化是通过将数据按照一定比例缩放，使之落入特定的区间，常用的方法有 Z-score 标准化和 Min-Max 标准化。

# Z-score标准化代码实现
def z_score_normalization(data):
    mean = np.mean(data, axis=0)
    std = np.std(data, axis=0)
    normalized_data = (data - mean) / std
    return normalized_data

#### 2.1.2 数据的协方差矩阵计算
在主成分分析中，计算数据的协方差矩阵是为了找出数据间的线性关系，从而进行主成分分析的下一步操作。

# 计算数据的协方差矩阵
def calculate_covariance_matrix(data):
    num_samples = len(data)
    mean_data = np.mean(data, axis=0)
    cov_matrix = (data - mean_data).T.dot(data - mean_data) / (num_samples - 1)
    return cov_matrix

### 2.2 奇异值分解（SVD）在主成分分析中的应用
奇异值分解（SVD）是一种将矩阵分解为特征向量和奇异值的方法，在主成分分析中有着广泛的应用。
#### 2.2.1 奇异值分解的原理
SVD可以将任意一个矩阵分解为三个矩阵的乘积，即：\[ A = U \Sigma V^T \]其中，U和V是正交矩阵，Σ是对角矩阵，对角线上的元素称为奇异值。

# 使用SVD进行主成分分析的代码示例
from numpy.linalg import svd

def pca_with_svd(data, num_components):
    U, s, Vt = svd(data)
    components = Vt[:num_components]
    projected_data = np.dot(data, components.T)
    return projected_data

#### 2.2.2 如何利用SVD求解主成分
通过SVD分解原始数据矩阵，可以得到投影矩阵Vt，将原始数据乘以Vt即可得到降维后的数据。
#### 2.2.3 SVD在主成分分析中的优势
SVD计算简单高效，在处理大规模数据时具有较好的表现，能够找到数据的最重要特征，是PCA的重要实现方式之一。

### 2.3 主成分分析中的特征值分解
主成分分析中的特征值分解是另一种常用的方法，用于求解数据的主成分和对应的特征值。
#### 2.3.1 特征值的求解方法
通过解矩阵的特征值问题，可以得到数据的特征值和对应的特征向量，进而进行主成分分析。

# 计算特征值和特征向量的代码示例
def calculate_eigen(data):
    cov_matrix = calculate_covariance_matrix(data)
    eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
    return eigenvalues, eigenvectors

#### 2.3.2 特征值分解与主成分分析的关系
特征值分解提供了数据的主成分和对应的重要程度，是PCA算法中决定保留哪些主成分的重要依据。
#### 2.3.3 特征值分解的意义及应用
通过特征值分解，可以找出数据集中最主要的特征和与之相关的主成分，有助于降低数据维度、提取有效特征。

通过上述章节内容的阐述，读者可以深入了解主成分分析的数学基础及相关算法应用，为接下来的实践应用打下坚实基础。

# 3. 主成分分析在数据降维中的应用

数据降维是处理高维数据的重要方法，通过减少特征维度来简化数据集，降低计算复杂度的同时保留数据的关键信息。

#### 3.1 数据降维的概念
在现实应用中，数据往往包含大量冗余信息或噪声，而主成分分析作为一种常用的数据降维技术，可以帮助我们更好地理解数据的内在结构。

数据降维的主要原因在于维度灾难和数据可视化。高维数据集往往容易导致维度灾难，增加了数据分析和处理的难度，而数据可视化又要求数据在二维或三维空间中表示，因此必须降低数据的维度。

#### 3.2 主成分分析及变换矩阵
主成分分析通过线性变换将原始特征空间转换为新的特征空间，其中，转换矩阵的选取是关键的一步。该矩阵由数据的特征向量构成，通过将数据投影到新的坐标系上来实现数据降维。

主成分分析还可以通过特征值的大小来确定各主成分的重要性，从而选择最重要的主成分作为数据集的子空间。这种方法能够更好地保留数据的主要信息，减少信息丢失带来的影响。

#### 3.3 主成分分析在特征提取中的应用
特征提取是机器学习任务中的一个关键步骤，通过提取数据的关键特征来减少数据的维度，简化模型，并提高模型的准确性和泛化能力。

主成分分析作为一种无监督学习方法，在特征提取中具有广泛的应用。它能够发现数据集中最具代表性的特征，从而帮助模型更好地理解数据，提高模型的鲁棒性和泛化能力。

主成分分析与模式识别任务密切相关，通过提取数据集中的主要特征，可以更好地描述数据的结构，识别数据中的模式，为后续的分类、聚类等任务提供有力支持。

### 数据降维流程示意图

graph LR
    A[原始数据集] --> B{数据预处理}
    B --> C[计算协方差矩阵]
    C --> D[特征值分解]
    D --> E{选择主成分个数}
    E --> F[构建变换矩阵]
    F --> G[数据投影]
    G --> H[降维后的数据集]

#### 数据降维的优势
- 减少计算成本：降低数据维度可以显著减少计算资源的消耗，提高训练和预测效率。
- 减少过拟合风险：降维可以减少特征数量，降低模型复杂度，降低过拟合的风险。
- 提高模型解释性：降维后的数据更容易理解和解释，有助于深入分析数据的特征和规律。

通过主成分分析进行数据降维，可以有效提高数据处理效率，简化模型复杂度，提高模型泛化能力，是机器学习领域中一种重要的数据预处理技术。

# 4. 高级主成分分析技术及进阶应用**

4.1 Kernel PCA及非线性主成分分析

Kernel PCA（Kernel Principal Component Analysis）是主成分分析的一种扩展，能够处理非线性数据集，通过核技巧将数据映射到高维空间，进而进行线性分析。非线性主成分分析则专注于捕捉数据中的非线性结构，对于复杂数据具有较好的表达能力。

Kernel方法在主成分分析中的应用：

# Kernel PCA 示例代码
from sklearn.decomposition import KernelPCA

kpca = KernelPCA(n_components=2, kernel='rbf')
X_kpca = kpca.fit_transform(X)

使用核函数（如径向基函数-RBF）将数据映射到高维空间，再进行主成分分析，可发现数据的非线性结构。

非线性主成分分析的概念及优势：
非线性主成分分析旨在发现数据中的非线性关系，与传统PCA相比，在处理非线性数据时表现更出色。通过捕获数据不同方向上的非线性特征，非线性PCA可更准确地揭示数据集的内在结构。

4.2 主成分分析在图像处理中的应用

图像数据的特性与主成分分析：
图像数据通常拥有高维度和复杂的内在结构，主成分分析可用于提取这些数据的主要特征，降低数据复杂度。在图像处理中，PCA可用于压缩图像、提取重要特征等。

主成分分析在图像压缩与特征提取中的应用：

# 图像压缩示例代码
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

# 原始图像矩阵
img = plt.imread('image.jpg')
# 将图像数据转化为向量
img_vec = img.reshape(-1, 3)
# PCA压缩
pca = PCA(n_components=50)
img_compressed = pca.fit_transform(img_vec)
# 重构图像
img_reconstructed = pca.inverse_transform(img_compressed).reshape(img.shape)

plt.imshow(img_reconstructed)
plt.axis('off')
plt.show()

通过PCA对图像数据进行压缩，可以保留主要特征信息，同时减少图像的存储空间。

4.3 主成分分析在金融数据分析中的应用

主成分分析在金融风险管理中的应用：
金融数据通常具有高度相关性，主成分分析可用于降维，提取关键特征，帮助识别风险和建立模型。通过PCA，金融机构可以更好地理解数据背后的模式和关联。

主成分分析在股票市场预测中的实践案例：
将股票市场的多维数据进行主成分分析，可以找到影响股价波动的主要因素，辅助投资者进行决策。通过挖掘数据中的潜在结构，PCA在股票市场预测中有着广泛的应用前景。

# 5. 主成分分析在生物信息学中的应用

本章将探讨主成分分析在生物信息学领域中的应用。生物信息学是一门交叉学科，涉及生物学、计算机科学和统计学等领域，而主成分分析作为一种数据降维技术，在生物信息学中有着广泛的应用。本章将详细介绍主成分分析在生物学数据处理、基因表达数据分析和蛋白质结构预测等方面的实际应用案例。

### 5.1 生物学数据处理中的主成分分析
生物学研究中常涉及到各种生物数据，如基因组数据、表达数据等，这些数据往往高维且复杂。主成分分析可以帮助研究人员挖掘数据中的潜在信息，发现数据之间的相关性和模式，从而更好地理解生物学系统的特征。以下是主成分分析在生物学数据处理中的具体应用场景：

- **基因表达数据分析**：通过主成分分析可以降低基因表达数据的维度，提取最具代表性的特征，从而帮助识别基因表达模式和生物过程中的关键因素。
- **序列比对与分类**：主成分分析可用于分析生物序列的相似性和差异性，帮助研究人员进行序列分类、亲缘关系分析等。
- **蛋白质结构预测**：利用主成分分析对蛋白质结构数据进行降维和特征提取，有助于预测蛋白质结构和功能，为药物设计等领域提供支持。

在生物信息学中，主成分分析的应用为研究人员提供了更深入的数据洞察和解释能力，有助于推动生物学知识的发现和应用。

### 5.2 生物信息学中的主成分分析案例分析
下面通过一个生物信息学中常见的案例来具体展示主成分分析在实际应用中的效果。我们以基因表达数据为例，通过主成分分析对基因表达谱进行分析和可视化：

# 导入所需库
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# 随机生成基因表达数据
data = np.random.rand(100, 10)

# 创建PCA对象并拟合数据
pca = PCA(n_components=2)
pca.fit(data)

# 可视化主成分分析结果
transformed_data = pca.transform(data)

plt.scatter(transformed_data[:, 0], transformed_data[:, 1])
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA on Gene Expression Data')
plt.show()

在以上代码中，我们通过随机生成的基因表达数据进行主成分分析，并将结果可视化展示在散点图中，以便更直观地理解数据的降维效果及不同样本间的分布情况。

### 5.3 生物信息学中的主成分分析流程图

graph LR
    A[收集生物信息学数据] --> B(数据预处理)
    B --> C{选择主成分数量}
    C -->|确定| D(应用PCA)
    C -->|不确定| E(调整参数)
    D --> F[数据分析与可视化]
    F --> G[得出结论与建议]

以上流程图展现了在生物信息学领域中应用主成分分析的一般流程：从数据收集和预处理开始，到最终的数据分析、结论得出与建议。主成分分析作为其中的重要一环，帮助研究人员更好地理解生物数据背后的信息与规律。

通过本章的介绍，读者可以更好地了解主成分分析在生物信息学中的应用，以及如何利用主成分分析技术处理和分析生物学数据，推动生物信息学领域的研究和应用发展。