【无线通信实践课堂】：多普勒效应模拟与实验，掌握核心技术


# 摘要
多普勒效应是波动与运动物体相互作用的物理现象，广泛应用于无线通信、雷达探测和卫星定位等领域。本文首先介绍了多普勒效应的基础理论和数学模型，随后详细讨论了其在不同频率（声波、电磁波、光波）下的表现形式，并介绍了仿真计算方法。在实验部分，文章设计了模拟实验来验证理论，并探讨了多普勒效应对无线通信技术中频率补偿、信号处理和定位精度的影响。最后，文章对实验结果进行了分析和验证，并提出了基于多普勒效应的教学实践策略，旨在提高学生对这一重要物理现象的理解和应用能力。

# 关键字
多普勒效应；数学模型；仿真计算；无线通信；教学实践；实验验证

参考资源链接：[无线通信理解：多径与多普勒效应深度解析](https://wenku.csdn.net/doc/4e6egu8got?spm=1055.2635.3001.10343)
# 1. 多普勒效应的基础理论

## 1.1 多普勒效应的定义

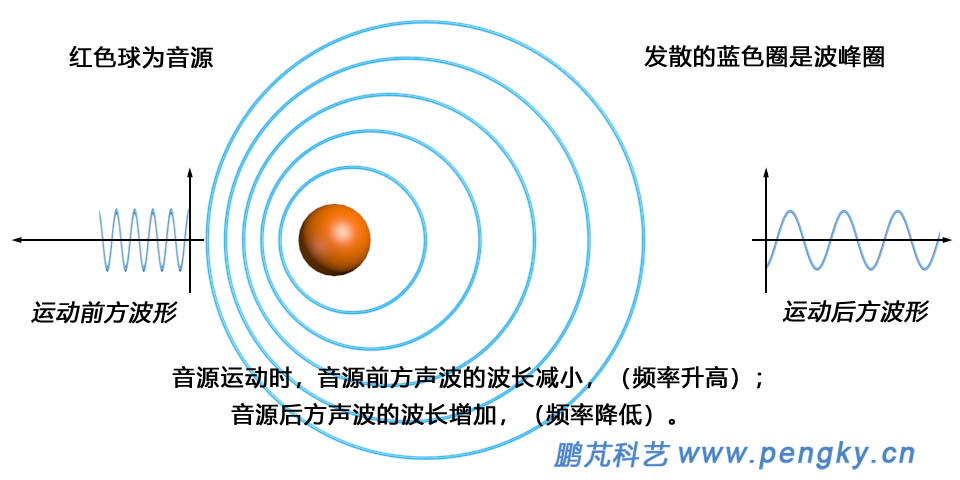
多普勒效应描述了波源和观察者之间的相对运动如何影响观察到的波频率。当波源和观察者之间存在接近或远离的相对运动时，观察者接收到的波频率与波源发出的波频率会有差异。这一效应适用于声波、电磁波等各种类型的波。

## 1.2 历史背景与发展

多普勒效应的概念最早由奥地利物理学家克里斯蒂安·多普勒于1842年提出。经过多年的实践验证和理论发展，多普勒效应已成为物理、工程学乃至天文学等多个领域的基础理论之一。

## 1.3 理论的实际意义

在实际应用中，多普勒效应可用于多种技术，如速度测量、定位、无线通信等。例如，在医疗领域，多普勒效应被用于超声波心动图来测量血流速度，而在交通领域，它可以用于监测车辆速度。

# 2. 多普勒效应的数学模型与计算

### 2.1 多普勒效应的数学表述

#### 2.1.1 传统多普勒效应公式推导

多普勒效应描述了观察者感知的波频率与波源频率之间由于相对运动产生的变化。为了理解这一点，我们需要推导出多普勒效应的基本数学公式。当波源和观察者相对静止时，观察者接收到的频率 \( f \) 与波源发出的频率 \( f_0 \) 是相同的。

当波源与观察者之间存在相对运动时，存在以下关系：

\[ f = \frac{v + v_0}{v + v_s} f_0 \]

这里，
- \( f \) 是观察者接收到的频率。
- \( f_0 \) 是波源发出的频率。
- \( v \) 是波在介质中的传播速度。
- \( v_0 \) 是观察者相对于介质的速度。
- \( v_s \) 是波源相对于介质的速度。

这个公式假设观察者和波源之间的相对速度是沿着两者连线的方向。在实际情况中，如果波源和观察者之间的相对速度有横向分量，则需要对公式进行相应的调整。

#### 2.1.2 非线性多普勒效应的理论扩展

在波源和观察者运动速度较低时，多普勒效应表现为线性关系。然而，当速度接近光速时，需要应用相对论效应进行修正。爱因斯坦的狭义相对论给出修正后的多普勒效应公式：

\[ f = f_0 \sqrt{\frac{1 + v/c}{1 - v/c}} \]

其中，
- \( c \) 是光速。
- \( v \) 是观察者相对于波源的相对速度。

### 2.2 多普勒效应在不同频率下的表现

#### 2.2.1 声波多普勒效应的特征

在日常生活中，最常见的多普勒效应例子是救护车的警笛声。当救护车向观察者驶来时，声波的频率增加，人们听到的是一个更尖锐的声音；而当救护车离去时，声波的频率减小，听起来声音变得低沉。

声波多普勒效应的频率变化可以由以下公式描述：

\[ f' = \frac{v}{v \pm v_s} f \]

其中，
- \( f' \) 是观察者接收到的频率。
- \( f \) 是声源发出的原始频率。
- \( v \) 是声波在空气中的传播速度。
- \( v_s \) 是声源相对于介质的速度。
- 正号适用于声源远离观察者的情况，负号适用于声源接近观察者的情况。

#### 2.2.2 电磁波多普勒效应的特征

在电磁波领域，多普勒效应同样重要，特别是在天文观测中。当恒星或星系远离地球时，它们发出的光波的波长会变长，表现为红移现象；而当它们接近时，波长变短，表现为蓝移现象。

电磁波的多普勒效应可以用相对论公式来描述，因为光速极快，经典力学的多普勒效应公式需要进行修正。

#### 2.2.3 光波多普勒效应与相对论效应

光波的多普勒效应可以通过考虑时间膨胀和长度收缩效应来理解，这些效应都是相对论的一部分。当光源远离观察者时，光波的波长变长，频率下降；当光源接近观察者时，波长缩短，频率增加。

这个现象可以通过以下公式描述：

\[ \Delta \lambda = \lambda' - \lambda = \frac{v \lambda'}{c} \]

其中，
- \( \Delta \lambda \) 是波长的变化。
- \( \lambda' \) 是接收时的波长。
- \( \lambda \) 是发射时的波长。
- \( v \) 是光源相对于观察者的速度。
- \( c \) 是光速。

### 2.3 多普勒效应的仿真计算方法

#### 2.3.1 数值模拟的基础

数值模拟是通过计算机执行数学模型的一种技术，它可以帮助我们更好地理解多普勒效应。在多普勒效应的数值模拟中，我们常常需要模拟波源和观察者之间的相对运动，计算出观察者接收到的频率变化。

为了进行这样的模拟，我们需要定义波源和观察者的位置、速度以及波在介质中的传播速度。在模拟过程中，我们可以通过时间步长来迭代计算出每个时间点的频率变化，并记录下来用于后续分析。

#### 2.3.2 计算软件的选择与应用

选择适合的数值模拟软件对于进行有效的多普勒效应模拟至关重要。软件需要能够处理复杂的数学计算，并能够生成准确的频率变化数据。

MATLAB是一个广泛使用的计算软件，它可以用来编写脚本并执行复杂的数学运算。通过MATLAB，我们可以构建多普勒效应的数值模型，利用内置的函数进行快速的数值计算，并使用绘图工具可视化结果。

下面是一个简单的MATLAB代码示例，用于模拟线性多普勒效应：

% MATLAB代码示例
% 假定波源频率f0，波速v，观察者速度v0，波源速度vs

f0 = 1000; % 波源频率（单位：Hz）
v = 343; % 声波在空气中的速度（单位：m/s）
v0 = 0; % 观察者速度（单位：m/s）
vs = 10; % 波源速度（单位：m/s）

% 时间步长和总模拟时间
dt = 0.001; % 时间步长（单位：秒）
total_time = 1; % 总模拟时间（单位：秒）

% 时间数组和对应的频率数组
time_array = 0:dt:total_time;
frequency_shift = zeros(size(time_array));

for i = 1:length(time_array)
    % 计算观察者接收到的频率
    frequency_shift(i) = f0 * (v / (v - vs));
end

% 绘制频率随时间变化的图像
plot(time_array, frequency_shift);
xlabel('Time (seconds)');
ylabel('Observed Frequency (Hz)');
title('Doppler Effect Simula