【操作系统中的补码原理：内存与进程管理的幕后】


参考资源链接：[补码运算详解：加法、乘法与溢出判断](https://wenku.csdn.net/doc/74q1vn5i6r?spm=1055.2635.3001.10343)
# 1. 补码原理概述

## 1.1 二进制数系统与计算机表示
计算机使用二进制数系统，它由0和1组成。在计算机的数字世界中，所有信息，包括数字、字符、图像等，最终都通过二进制形式进行存储和处理。理解补码需要首先掌握二进制表示方法。

## 1.2 补码的概念与引入原因
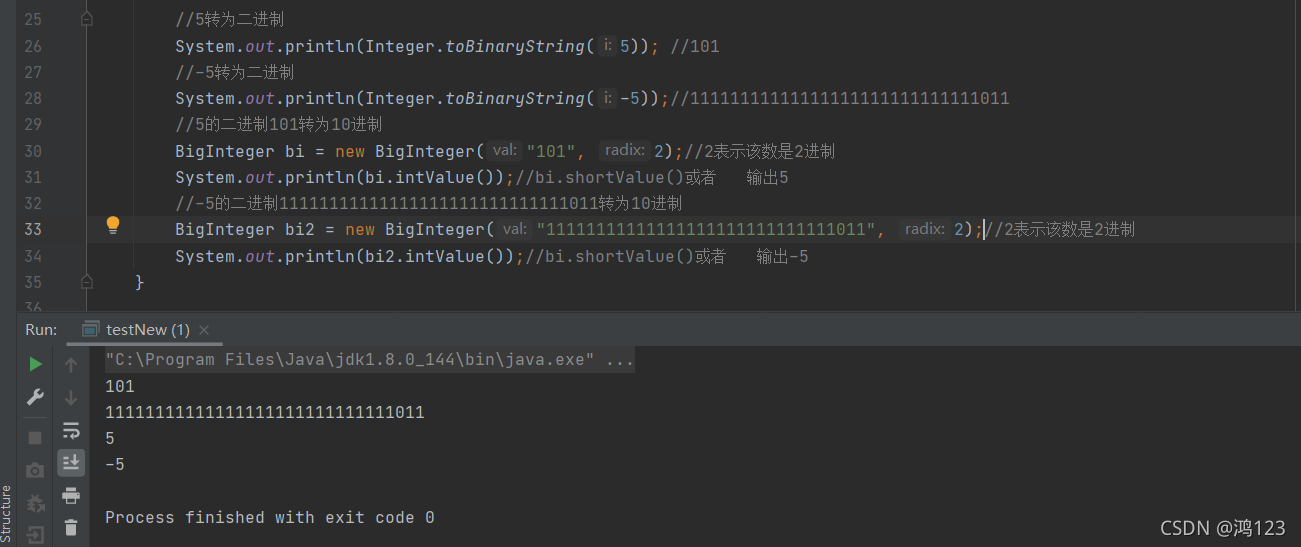
补码是计算机中表示有符号整数的一种方式，它的出现解决了二进制数系统中的符号表示和运算问题。为了能够使用相同的电路进行加法和减法运算，补码引入了反码和补码的概念。正数的补码与其原码相同，而负数的补码是其反码加1。

## 1.3 补码的数学意义和实际应用
补码不仅仅是一种数学上的表示方法，它在实际的计算机系统中具有重要的应用。在硬件层面，使用补码可以简化计算机加法器的设计；在软件层面，补码帮助程序员编写更加简洁和高效的代码。

graph TD
    A[计算机表示] --> B[二进制数系统]
    B --> C[补码的概念]
    C --> D[补码的数学意义]
    D --> E[补码的实际应用]

接下来的章节将会深入探讨补码与计算机算术、内存管理、进程调度之间的联系，以及在实际编程语言和操作系统中的应用与实践案例。

# 2. ```
# 第二章：补码与计算机算术

补码不仅是计算机系统中表示和存储整数的基础，而且在各种算术运算中扮演了至关重要的角色。在深入探讨补码与计算机算术的关系之前，我们先要理解补码的基础概念。

## 2.1 补码的基础概念

### 2.1.1 正数与负数的表示方法

在计算机系统中，整数是通过二进制位序列来表示的。一个固定长度的二进制数可以表示的整数范围是有限的，这取决于位数。例如，一个8位的二进制数可以表示的整数范围从0到255，使用补码表示则从-128到127。正数通常按其正常的二进制形式表示，而负数则采用补码形式。

为了表示负数，计算机使用了二进制的补码表示法。在补码系统中，负数是通过对对应的正数的二进制表示取反（将1变为0，将0变为1）然后加1得到的。例如，假设我们有8位二进制数，那么-1的补码表示如下：

00000001 (1的正常二进制表示)
11111110 (取反)
+ 00000001
11111111 (-1的补码表示)

### 2.1.2 补码的定义和特性

补码是一种数的编码方式，用于简化二进制运算，特别是加法和减法运算。在补码系统中，0有唯一的表示，最小的负数是一个全1的数，然后是全1加1的表示方法来表示-1。这种表示方法的特点是：

- 正数和0的补码与其原码相同。
- 负数的补码是其原码除符号位外所有位取反后加1。
- 补码系统中的加法可以通过简单的按位加法来完成，无需额外的逻辑来处理正负号。

## 2.2 补码在算术运算中的应用

### 2.2.1 加法与减法的补码实现

在计算机中执行加法运算时，可以直接使用补码进行。例如，8位二进制数-1加上1的过程如下：

11111111 (-1的补码表示)
+ 00000001 (1的补码表示)
100000000 (结果为9位，左边的1是进位，丢弃)

因为结果超出了8位的表示范围，所以最高位的进位被丢弃，这叫做模2加法，结果是8位补码表示的-0，也就是0。补码系统中，加法和减法可以统一处理：减去一个数，等价于加上该数的补码。

### 2.2.2 乘法与除法的补码优化

补码在乘法和除法运算中的应用稍微复杂一些，但依然基于相同的原理。在乘法运算中，计算机通过位移和加法来实现乘法过程，可以通过补码来优化某些步骤。例如，对于两个负数相乘，可以先将两个数转换为正数进行乘法运算，再根据结果的符号位来确定最终结果的符号。

在除法运算中，可以通过补码来确定商和余数。这里涉及到一些更复杂的算法，通常由硬件直接支持，优化乘法和除法运算时的性能。

## 2.3 补码运算的边界情况处理

### 2.3.1 溢出的检测与处理

在补码系统中，当一个算术运算的结果超出了其能够表示的范围时，就会发生溢出。溢出检测对于确保程序的正确性和稳定性至关重要。在计算机硬件中通常会有专门的溢出标志位来指示溢出的发生。

例如，在一个8位的系统中，如果试图计算255加1的结果，将得到：

11111111 (255的补码表示)
+ 00000001 (1的补码表示)
1 00000000 (左边的1是进位，9位结果超出8位表示范围)

由于结果是9位，最高的9位（最高位进位）被丢弃，而硬件会设置溢出标志位，指示计算结果不正确。

### 2.3.2 符号扩展和位截断的影响

在处理不同长度的整数时，经常需要将一个较短的数转换为较长的数，或者反过来，这涉及到符号扩展和位截断的处理。符号扩展是将一个负数的补码保持其符号位不变，同时将高位补为1，以保持其负数值；位截断则是忽略超出目标长度的高位。

例如，将-1的8位补码扩展为16位补码：

原8位补码：11111111
扩展为16位：1111111111111111

对于正数，符号扩展简单地在高位补0。位截断则可能引入失真，因为如果截断的位包含重要的数值信息，那么结果将不再是原来的数。

在实际操作中，补码的这些特性和处理方法需要通过具体的编程语言和指令集来实现。了解这些原理对于设计和优化算法、编写高效安全的代码至关重要。

通过本章节的介绍，读者应能深刻理解补码在计算机算术中的核心作用，及其如何在实际计算机系统中进行整数的表示与运算。在接下来的章节中，我们将探讨补码在内存管理和进程调度中的作用，进一步展示补码在计算机科学中的广泛应用。

# 3. 补码在内存管理中的角色

## 3.1 内存地址的补码表示
在现代计算机系统中，内存地址的管理是一项核心任务。内存地址的补码表示不仅用于虚拟内存与物理内存的映射，而且在计算过程中发挥着至关重要的作用。

### 3.1.1 虚拟内存与物理内存的映射
虚拟内存允许系统中的每个进程访问比实际物理内存更大的地址空间，这一映射过程可以通过补码高效实现。虚拟地址到物理地址的转换，涉及到页表和页表项的概念。

例如，当我们需要将虚拟地址转换为物理地址时，我们会通过页表项来完成。页表项通常包含了以下信息：

- 存在位（Present bit）: 指示该页表项是否在内存中。
- 读写位（Read/Write bit）: 指示是否可以对内存页进行读写操作。
- 用户/内核位（User/Kernel bit）: 区分内存页是用户空间还是内核空间。

通过补码可以简洁地表示和计算这些信息，并确保内存管理的高效性。

### 3.1.2 内存地址的补码转换与计算
在内存地址的转换计算中，补码用于表示负的偏移量或地址。由于计算机使用补码表示负数，对于内存地址的偏移操作，补码机制可以确保算术操作的正确性。

例如，在32位系统中，虚拟地址通常通过补码进行计算：

// 假设这是32位系统中的偏移量计算
int32_t virtualAddress = 0xFFFFFFF0; // 补码表示-16
int32_t offset = -16;
assert(virtualAddress == offset); // 通过断言验证补码表示与直接赋值是否一致

在实际的地址转换过程中，处理器会使用补码进行算术计算，确定物理地址。

## 3.