HFSS波导仿真在通信系统中的应用:理论与实践深度剖析
发布时间: 2024-12-24 19:02:25 阅读量: 10 订阅数: 12 


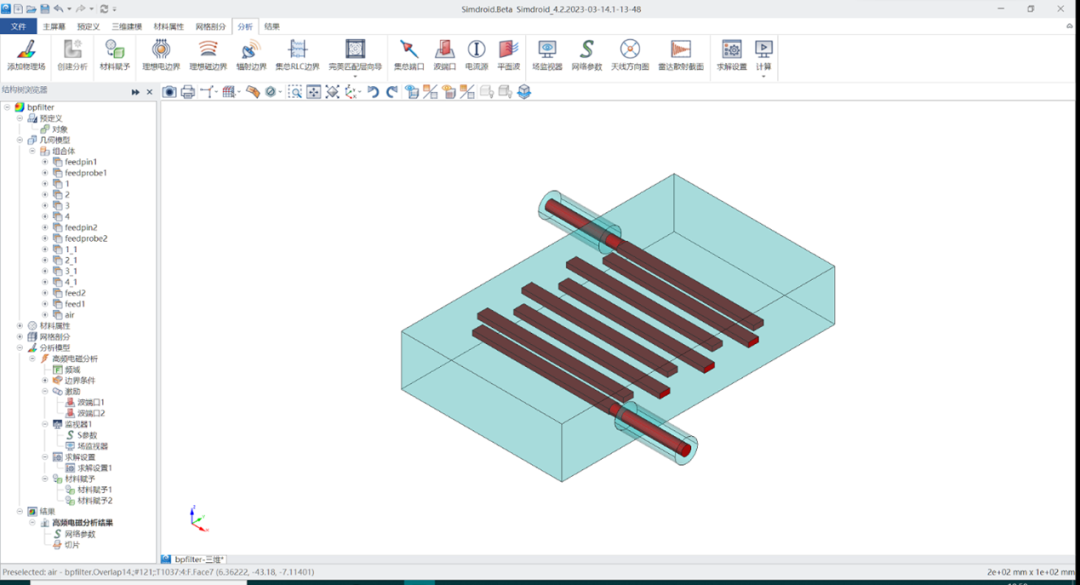
通信与网络中的波导缝隙天线的设计仿真
# 摘要
本文系统介绍了HFSS(High Frequency Structure Simulator)波导仿真技术的基础知识、理论基础、操作流程、应用案例以及高级技巧,并展望了该技术的未来发展方向。通过对波导工作原理、电磁波模式以及HFSS软件功能的详细介绍,为读者提供了波导仿真设计与分析的全面视角。文章详细阐述了从仿真设计准备到结果分析验证的完整流程,并通过具体的波导滤波器、耦合器及天线系统应用案例,展示了HFSS波导仿真的实用性。最后,文章还探讨了参数化分析、多物理场耦合仿真方法以及人工智能和高性能计算在仿真领域的应用,为波导仿真技术的持续创新提供了见解。
# 关键字
HFSS波导仿真;电磁理论;仿真设计;S参数分析;参数化优化;多物理场耦合;人工智能仿真;高性能计算
参考资源链接:[hfss波导仿真实验.pdf](https://wenku.csdn.net/doc/645d905b95996c03ac434412?spm=1055.2635.3001.10343)
# 1. HFSS波导仿真基础介绍
在现代通信和电子系统中,波导作为高效的能量传输介质发挥着至关重要的作用。为了优化波导设计并确保其性能达到预期标准,采用高频结构仿真软件(HFSS)进行波导仿真是必不可少的步骤。HFSS基于有限元方法(FEM)提供精确的三维电磁场仿真,是研究和设计波导组件的强大工具。本章节将简要介绍波导仿真的基本概念,为读者建立理论基础并展望后续章节的深入讨论。让我们从波导仿真在现实应用中的重要性以及HFSS软件的模拟优势开始。
# 2. HFSS波导仿真的理论基础
波导作为微波和射频系统中不可或缺的组成部分,承载着信号的传输。HFSS(High Frequency Structure Simulator)是一款强大的三维电磁场仿真软件,广泛应用于波导仿真领域。理解HFSS波导仿真的理论基础是进行精确仿真的关键。
## 2.1 波导的电磁理论
### 2.1.1 波导的工作原理
波导是一个封闭或半封闭的金属通道,它支持电磁波的传播。波导中的电磁波模式由边界条件决定,仅特定频率的波能够在波导内稳定传播。这种现象是由于波导内的壁面存在金属反射,产生驻波,形成特定的波模。波导中的信号传播利用的是导波模式,这与自由空间中电磁波的传播有着本质的区别。
### 2.1.2 波导中的电磁波模式分析
波导中的电磁波模式可以通过 Maxwell 方程组在边界条件下求解得出。波导内传播的模式分为TE模式(横电模式)和TM模式(横磁模式),以及TEM模式,但后者在大多数波导中不常见,因为TEM模式需要波导两端开放,无法形成闭合的导体表面。在工程实践中,最常用的是TE模式和TM模式,它们具有不同的截止频率,波导的尺寸、工作频率和传输特性决定了哪种模式将被激发。
## 2.2 HFSS软件基础
### 2.2.1 HFSS软件界面和功能概述
HFSS软件提供了一个交互式的图形用户界面,允许用户通过直观的界面完成复杂的建模和仿真任务。HFSS的核心功能包括:几何建模、材料属性定义、边界条件设置、网格划分、仿真求解以及后处理分析等。用户可以通过定义几何形状、分配材料属性、设置边界条件和激励源,来构建仿真模型。
### 2.2.2 HFSS中的材料和边界条件设置
在HFSS中定义材料属性时,需要根据材料的实际电性能输入介电常数、磁导率、损耗因子等参数。软件内置了大量材料库,用户也可自定义材料。边界条件在波导仿真中至关重要,决定了电磁波如何在波导内传播和反射。HFSS提供了多种边界条件,例如理想导体边界、辐射边界等,以模拟波导的不同物理情况。
## 2.3 波导仿真模型的建立
### 2.3.1 波导结构的设计与参数化
波导结构的设计是仿真过程的第一步。对于参数化的波导设计,HFSS支持通过变量驱动设计。用户可以定义几何参数作为变量,并在仿真过程中进行调整。通过参数化设计,可以方便地进行波导尺寸优化,快速得到最佳设计结果。
### 2.3.2 激励源和端口的设置方法
在HFSS中设置激励源和端口是至关重要的一步,它们决定了电磁波在波导内的激励方式和传输特性。根据实际应用场景,用户可以选择合适的激励源,如连续波(CW)源、脉冲源等。端口设置包括定义端口的类型、大小和方向,以及端口的激励条件。正确的端口设置能够确保波导的激励模式与实际应用匹配,是准确获取仿真结果的前提。
在设计波导时,还需考虑波导的物理特性和工作环境,如波导的长度、宽度、高度以及损耗特性等。通过深入理解波导的工作原理和HFSS软件的操作,工程师可以更有效地进行波导仿真,为后续的优化和验证工作打下坚实的基础。
# 3. HFSS波导仿真流程详解
## 3.1 仿真设计前的准备
### 3.1.1 仿真目标和要求的明确
在开始任何仿真工作之前,首要任务是明确仿真的目标和具体要求。这包括预期的结果、要验证的性能参数以及设计中必须满足的任何物理或电气约束。对于HFSS波导仿真,这些信息将指导我们选择合适的波导类型、确定正确的激励设置以及设定合理的仿真参数。例如,在设计一个滤波器时,我们可能需要关注其通带和阻带特性;而在设计耦合器时,则可能更关注其耦合度和隔离度。明确这些目标和要求有助于优化设计流程,提升仿真效率,减少不必要的迭代次数。
### 3.1.2 仿真参数的设定与网格划分
在HFSS中设定仿真参数是关键步骤之一。仿真参数包括频率范围、求解器类型、边界条件等。它们决定了仿真环境的设置,并影响到仿真的精度和速度。例如,在波导仿真中,一个重要的参数是求解器类型,通常使用本征模求解器(Eigenmode Solver)来进行模式分析,使用有限元法(Finite Element Method, FEM)求解器来计算电磁场分布。
网格划分是另一个重要步骤,它涉及到将连续的物理结构离散化为有限个单元的过程。在HFSS中,网格划分需要特别注意,因为它直接影响仿真的准确性和计算资源的使用。通常,网格越细,仿真的精度越高,但计算时间也相应增加。因此,一个好的做法是在保证结果准确性的前提下,尽可能地优化网格划分以减少计算量。
## 3.2 仿真过程的操作步骤
### 3.2.1 求解器类型的选择和配置
HFSS提供了多种求解器类型,包括模式求解器、时域求解器和频域求解器等,针对不同的仿真目标和场景进行选择。例如,模式求解器适用于分析波导中的传播模式,而频域求解器适用于计算和分析频率依赖性问题。
配置求解器时,需要设置仿真频率范围、收敛标准、迭代次数等参数。这些设置决定了求解器的计算精度和速度。在波导仿真中,通常会根据波导的特性和预期的工作频率范围来选择合适的求解器,并进行细致的配置以确保仿真结果的准确性。
### 3.2.2 仿真执行和监控
完成求解器的配置后,即可执行仿真。在仿真过程中,需要监控仿真状态和结果,以确保仿真按预期进行。HFSS提供了实时的仿真监控功能,包括收敛图表和字段监控器。这些工具可以帮助用户评估仿真是否收敛,以及在何处出现可能的问题。
在仿真执行过程中,也可能遇到需要调整的情况。例如,如果仿真没有达到预定的收敛标准,则可能需要增加迭代次数,或者优化网格划分。有时,也需要对激励源或边界条件进行微调,以确保仿真环境的准确性。
## 3.3 结果分析与验证
### 3.3.1 S参数的提取和分析
波导仿真的一个关键结果是S参数,它描述了波导端口间的散射特性。在HFSS中,可以自动提取S参数,并进行详细分析。S参数通常以图表的形式展现,例如幅度和相位随频率变化的曲线。
在分析S参数时,需要关注波导的谐振频率、带宽和损耗等特性。谐振频率表示波导支持的特定频率,带宽与波导的应用场景有关,而损耗则与波导材料和结构密切相关。通过分析S参数,我们可以评估波导的设计是否满足预定的电气要求,以及是否需要进行优化。
### 3.3.2 电磁场分布的可视化
除了S参数,电磁场分布也是波导仿真的重要结果。HFSS可以提供多种方式来可视化波导内部的电磁场分布,包括电场和磁场分布图、电流和电荷密度分布图等。这些可视化工具对于理解波导内部的电磁现象以及波导结构的性能至关重要。
通过电磁场分布的可视化,设计师可以直观地识别波导中可能出现的问题,如高损耗区域、不期望的模式激发或者电磁干扰等。这有助于设计师进一步优化波导设计,确保其在实际应用中的性能。
为了实现上述内容,以下是一个简化的示例代码块,展示了如何在HFSS中进行一个基本的波导仿真,并提取和分析S参数。
```hfss
# HFSS Simulation Script Example
# Create a simple rectangular waveguide
boxWaveguide = hfss.CreateBox('Waveguide', 30, 15, 10, 'Center', [0, 0, 0])
# Set the material properties of the waveguide
hfss.SetMaterial('Waveguide', 'Copper')
# Define the simulation frequency range
freqRange = [2e9, 18e9] # 2 GHz to 18 GHz
# Setup the eigenmode solver for the fundamental mode analysis
solverSetup = hfss.CreateEigenmodeSetup(
```
0
0





