【排序算法性能大战】：从冒泡到快速排序，一探究竟


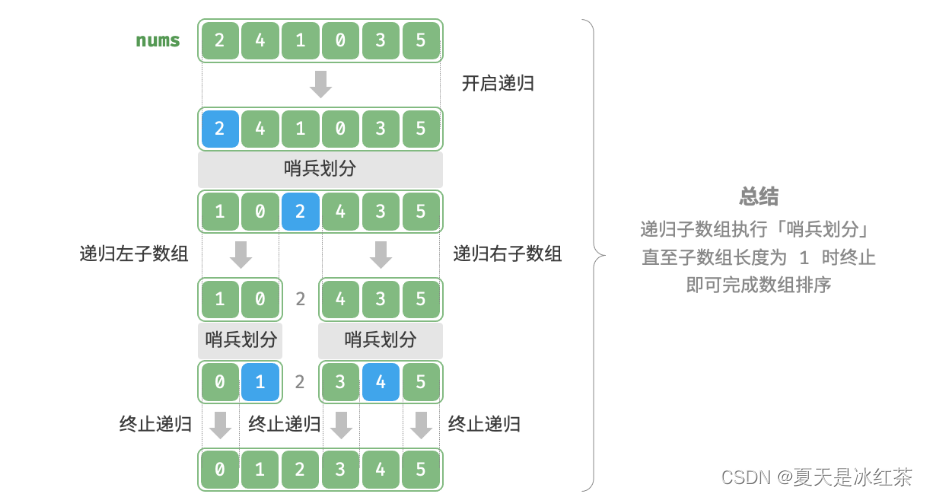
# 摘要
排序算法是计算机科学中不可或缺的一部分，对数据处理的效率有着重要影响。本文首先介绍了排序算法的基础知识，包括其重要性、基本概念以及性能评估指标。随后，针对冒泡排序、插入排序、归并排序和快速排序这四种常见算法，本文深入探讨了它们的理论原理、实现方法、性能分析以及优化策略。通过对比分析，本文提出了在不同应用场景下选择合适排序算法的指南，并对排序算法的未来发展趋势进行了展望，为高效算法的设计和应用提供了参考。

# 关键字
排序算法；冒泡排序；插入排序；归并排序；快速排序；性能分析；算法选择

参考资源链接：[数据结构1800题：考研必备PDF习题集](https://wenku.csdn.net/doc/6ffwf0s7q8?spm=1055.2635.3001.10343)
# 1. 排序算法基础介绍

排序算法是计算机科学中不可或缺的一部分，它们在数据处理、数据库管理、搜索算法和许多其他应用中扮演着核心角色。理解不同排序算法的优劣，对于提升程序性能和处理效率至关重要。

## 1.1 排序算法的重要性

### 1.1.1 排序算法在计算机科学中的地位
排序算法是算法基础，它涉及到数据的组织和存储，提高数据检索效率。在计算机科学的各个领域，如数据库、操作系统和人工智能，排序算法都占有举足轻重的地位。一个高效的排序算法可以显著减少数据处理时间，提高程序性能。

### 1.1.2 排序算法的常见应用场景
排序算法被广泛应用于各种场景，例如，电子商务网站的商品排序、搜索引擎的结果排序、数据库中记录的索引排序等。这些场景对排序算法的时间复杂度和空间复杂度有明确的要求，从而决定了使用哪种排序方法更为合适。

## 1.2 排序算法的基本概念

### 1.2.1 时间复杂度和空间复杂度
时间复杂度和空间复杂度是衡量排序算法性能的两个关键指标。时间复杂度表征了算法完成任务所需的操作次数，而空间复杂度则反映了算法在运行过程中所占用的额外空间大小。不同的排序算法在这些指标上有不同的表现，比如冒泡排序的时间复杂度较高，而快速排序在最坏情况下仍然是 O(n log n)。

### 1.2.2 稳定性、内排序与外排序
排序算法的稳定性是指算法能否保持相同值的元素的相对顺序。内排序是指所有排序操作都在内存中进行，而外排序则涉及外部存储（如硬盘）。不同的应用场合对排序的稳定性及内外排序有不同的要求，理解这些概念对于正确选择和实现排序算法至关重要。

本章内容为后续的实践操作和深入讨论奠定了基础，将在后续章节中，我们将会详细探讨各种排序算法的原理和实践应用。

# 2. 冒泡排序的理论与实践

## 2.1 冒泡排序的工作原理
冒泡排序是一种简单的排序算法，它重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

### 2.1.1 算法步骤详解
冒泡排序的基本步骤如下：
1. 比较相邻的元素。如果第一个比第二个大（升序），就交换它们两个。
2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

### 2.1.2 时间复杂度和空间复杂度分析
冒泡排序的时间复杂度分为最好、最坏和平均三种情况：
- 最好情况：输入数组已经是正序的（O(n)）。
- 最坏情况：输入数组是逆序的（O(n^2)）。
- 平均情况：(O(n^2))。

空间复杂度为 O(1)，因为冒泡排序是原地排序算法，除了输入数组不需要额外的存储空间。

## 2.2 冒泡排序的代码实现
### 2.2.1 基本实现
以下是一个简单的冒泡排序的代码实现：

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

### 2.2.2 优化策略和代码改进
冒泡排序可以进行优化，加入一个标志位，如果在一趟遍历中发生了交换，则说明有元素未排序好，否则可以提前结束排序：

def optimized_bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        swapped = False
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
                swapped = True
        if not swapped:
            break
    return arr

## 2.3 冒泡排序的实践应用
### 2.3.1 实际问题中的应用实例
在实际应用中，冒泡排序通常不被推荐用于大数据量的排序，因为它效率较低。然而，在数据量较小或者几乎有序的情况下，冒泡排序可以作为快速实现的方法之一。例如，一些简单的脚本或教学演示。

### 2.3.2 冒泡排序与其他算法的比较
与其他排序算法相比，如快速排序、归并排序，冒泡排序的效率较低。但是，它具有实现简单、原地排序（不需要额外空间）等优点。这使得在特定情况下，冒泡排序仍有一定的应用价值。

### 表格展示
以下是冒泡排序与其他排序算法的性能对比：

| 算法 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 特点 |
|------|----------------|----------------|----------------|------------|------|
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 简单、稳定，但效率较低 |
| 快速排序 | O(n log n) | O(n^2) | O(n log n) | O(log n) | 快速、不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定、效率适中 |

以上内容完成了对冒泡排序的理论基础、代码实现以及应用场景的详细介绍，为读者提供了一个全面的冒泡排序学习视角。

# 3. 插入排序与归并排序的深入分析

## 3.1 插入排序的理论基础
### 3.1.1 算法描述和步骤
插入排序是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常使用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

其算法描述如下：
1. 从第一个元素开始，该元素可以认为已经被排序
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
5. 将新元素插入到该位置后
6. 重复步骤2~5

### 3.1.2 插入排序的性能评估
插入排序在最好情况下（输入数组已经是正序）的时间复杂度为O(n)，在最坏情况下（输入数组为逆序）的时间复杂度为O(n^2)，在平均情况下也是O(n^2)。其空间复杂度为O(1)，因为只需要常数空间。

### 3.1.3 插入排序的性能特点和代码实现
插入排序的优点是简单易于实现，且在部分场景下如数据量小或者基本有序的情况下，效率较高。它的缺点是在数据量大且序列混乱时，性能表现不佳。

下面是一个插入排序的Python代码实现：

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i-1
        while j >=0 and key < arr[j]:
            arr[j+1] = arr[j]
            j -= 1
        arr[j+1] = key
    return arr

执行逻辑说明：该实现的核心是一个内层循环，它不断地将新元素与已排序部分的元素从后向前比较，必要时将其向后移动，直到找到合适的位置插入。

## 3.2 归并排序的原理与实现
### 3.2.1 归并排序的分治策略
归并排序是采用分治法的一个非常典型的应用。它将数组分成两半进行排序，递归地将每半再分成两半，直到每个子序列只有一个位置，此时认为子序列已排序。然后将各个子序列合并成有序序列。它的基本步骤是：
1. 将序列分成两部分，进行归并排序
2. 将排序好的两个子序列合并成一个最终的排序序列

### 3.2.2 归并排序的代码实现
下面是一个归并排序的Python代码实现，采用了递归分治的方法：

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        left_half = arr[:mid]
        right_half = arr[mid:]

        merge_sort(left_half)
        merge_sort(right_half)

        i = j = k = 0

        while i < len(left_half) and j < len(right_half):
            if left_half[i] < right_half[j]:
                arr[k] = left_half[i]
                i += 1
            else:
                arr[k] = right_half[j]
                j += 1
            k += 1

        while i < len(left_half):
            arr[k] = left_half[i]
            i += 1
            k += 1

        while j < len(right_half):
            arr[k] = right_half[j]
            j += 1
            k += 1

    return arr

执行逻辑说明：该代码定义了一个`merge_sort`函数，它递归地对数组的左右两半进行排序，然后通过一个合并函数将两个排序好的半部分合并。合并过程是将两个有序序列中的最小元素依次选出，直到一个序列为空，剩余的元素自然就是有序的。

## 3.3 实践中的应用对比
### 3.3.1 插入排序与归并排序的场景选择
在实际应用中，插入排序适用于数据规模较小且数据较为接近有序的情况，因为它在数据量小或几乎有序的情况下表现良好。而归并排序则适用于需要稳定排序的场景，它能够保证稳定的排序特性，并且具有较好的时间复杂度，在数据规模较大且无序程度较高的情况下也能保持较高的效率。此外，归并排序是外部排序的常用方法，适合于大量数据的排序。

### 3.3.2 实际案例分析
下面通过一个实际的案例来分析两种排序算法的效率和适用性。假设我们有一个包含1000个整数的数组，这些整数是随机生成的。

使用插入排序：

import random

# 创建一个随机数组
array = [random.randint(0, 10000) for _ in range(1000)]
insertion_sort(array)

使用归并排序：

import random

# 创建一个随机数组
array = [random.randint(0, 10000) for _ in range(1000)]
merge_sort(array)

通过这个案例，我们能够观察到归并排序比插入排序在执行时间上表现更为优越，尤其是随着数组大小的增加，这一差异会更加明显。此外，归并排序的可扩展性比插入排序要好，因为它不是原地排序，因此它可以用于大型数据集，而无需担心内存限制。

通过以上章节内容，我们可以得出结论：插入排序和归并排序各有优劣，其选择需根据实际问题的需求和数据的特性来决定。

# 4. ```
# 第四章：快速排序的原理与优化策略

快速排序是一种高效的排序算法，由C. A. R. Hoare在1960年提出。它采用了分而治之的策略来把一个序列分为较小和较大的两个子序列，然后递归地排序两个子序列。其核心在于分区操作，通过选取出一个基准元素（pivot），然后重新排列序列，使得所有比基准小的元素都排在它的前面，而所有比基准大的元素都排在它的后面。基准元素到位后，再递归地将小的和大的子序列独立地排序。

## 4.1 快速排序的基本概念
### 4.1.1 快速排序的原理和步骤
快速排序的核心步骤包括分区（partitioning）和递归（recursion）两个部分。分区是将数据划分为两个部分，一个包含所有小于基准元素的记录，另一个包含所有大于基准元素的记录。然后，对这两个部分递归地进行快速排序。

**分区步骤：**
1. 选择基准元素：通常可以从数据的两端开始，或者随机选择一个元素。
2. 重新排列元素：让所有比基准小的元素移到基准的左边，比基准大的元素移到右边。这个操作结束时，基准元素处于其最终位置。
3. 分区结果：基准左边的元素都不大于它，基准右边的元素都不小于它。

**递归排序步骤：**
1. 对基准左边的子序列进行快速排序。
2. 对基准右边的子序列进行快速排序。

### 4.1.2 快速排序的性能特点
快速排序的平均时间复杂度为O(n log n)，在大多数情况下表现非常优秀，尤其是在随机排列的数据集上。它特别适合大数据量的排序任务。快速排序的最坏情况时间复杂度为O(n^2)，这通常发生在数组已经是正序或逆序的情况下，此时可以选择随机化基准元素来避免。

## 4.2 快速排序的代码实践
### 4.2.1 标准快速排序算法实现
下面是一个快速排序的基本实现代码（假设数组为A，左边界为left，右边界为right）：

def quicksort(arr, low, high):
    if low < high:
        pivot_index = partition(arr, low, high)
        quicksort(arr, low, pivot_index - 1)
        quicksort(arr, pivot_index + 1, high)

def partition(arr, low, high):
    pivot = arr[high]
    i = low - 1
    for j in range(low, high):
        if arr[j] < pivot:
            i += 1
            arr[i], arr[j] = arr[j], arr[i]
    arr[i + 1], arr[high] = arr[high], arr[i + 1]
    return i + 1

### 4.2.2 常见优化方法和改进策略
快速排序有多种优化方法，以减少不必要的交换和增加算法的效率：

1. **尾递归优化**：采用尾递归的方式来优化递归调用栈的使用。
2. **三数取中法**：从区间的首、中、尾三个位置取样并比较取中间值作为基准元素，以减少最坏情况发生的概率。
3. **插入排序结合**：对小规模数据使用插入排序进行优化，因为插入排序在小规模数据上效率较高。
4. **并行排序**：针对现代多核处理器，可对不同子序列同时进行排序，提高效率。

## 4.3 快速排序的深入分析
### 4.3.1 不同基准选择的影响
基准元素的选择对快速排序的性能有很大影响，特别是在数据已经部分排序或重复元素较多的情况下。随机选择基准可以减少最坏情况发生的概率。

### 4.3.2 快速排序与其他算法的对比研究
与其他排序算法相比，快速排序通常在平均情况下最为高效，尤其是在需要稳定性的场合，它的优势更加明显。对于部分排序的数据，归并排序可能更优，而堆排序在极端情况下保持较好的性能表现。

总结快速排序，作为排序算法中的佼佼者，它的平均性能卓越，适用于大数据集。然而，它的最坏情况表现需要通过优化来避免。了解其工作原理和性能特点，可以帮助我们在实际应用中更好地选择和调整算法。

# 5. 综合比较与排序算法选择指南

## 5.1 各种排序算法的综合比较

排序算法的选择在不同的应用场景中起着至关重要的作用。在这一部分，我们将对之前章节介绍的算法进行一个全面的对比分析，帮助理解在什么情况下，某种排序算法会比其他算法表现得更好。

### 不同场景下的算法选择

不同的排序算法有着不同的时间和空间复杂度。例如，对于小规模数据集，简单直观的冒泡排序可能是快速而简便的选择，尽管它在时间复杂度上不如其他更先进的算法。而对于需要稳定排序的场合，比如在处理带有属性信息的记录时，插入排序可能更为适用。

对于大规模数据，快速排序可能是首选，因为它平均情况下的时间复杂度为O(n log n)，且实现起来相对简单。如果数据集已经部分排序，插入排序可能比快速排序更有效率。归并排序则保证了稳定的排序结果，并且在某些特定情况下，比如外部排序时，表现优异。

### 排序算法的优缺点总结

快速排序
优点：平均情况下效率高，空间复杂度低。
缺点：最坏情况下的时间复杂度较高，不稳定排序。

冒泡排序
优点：易于实现，对小数据集效率可接受。
缺点：时间复杂度较高，不适合大规模数据。

插入排序
优点：对于部分有序的数据集效率很高，稳定排序。
缺点：不适合大规模数据，时间复杂度为O(n^2)。

归并排序
优点：稳定排序，适合大规模数据，时间复杂度为O(n log n)。
缺点：空间复杂度较高，需要额外空间。

## 5.2 排序算法的选择标准和建议

根据具体需求来选择合适的排序算法，是提高程序性能的关键。下面提供一些建议帮助在实际开发中作出更明智的选择。

### 如何根据实际情况选择排序算法

- 数据规模：对于小规模数据，可以考虑简单直观的算法如冒泡排序或插入排序；对于大规模数据，建议使用快速排序或归并排序。
- 是否需要稳定排序：如果需要维持相等元素的顺序，则应选择稳定排序算法，如归并排序。
- 实现复杂度：快速排序虽然性能优秀，但实现起来比插入排序复杂。
- 预处理知识：如果数据部分有序，可优先考虑插入排序。

### 算法选择的最佳实践和建议

- 预先分析数据：在程序中加入数据预处理分析，根据数据特性选择排序算法。
- 使用高效的库函数：大多数编程语言的库都提供了高效的排序算法实现，建议优先使用。
- 性能测试：在不同的数据集上测试不同排序算法的性能，根据测试结果选择最适合的。

## 5.3 未来排序算法的发展趋势

随着计算机科学的发展，新的排序算法不断出现，它们试图解决传统排序算法的不足，提供更优的性能。

### 新型排序算法的探索

研究者们在探索新型的排序算法，如并行排序、分布式排序等，它们能更好地适应现代多核处理器和大规模数据集。此外，量子排序算法和非比较排序算法（如计数排序、基数排序）的研究也在进行，这些算法在特定条件下能提供突破性的性能提升。

### 排序算法在新兴领域的应用前景

排序算法不仅用于传统的数据处理，它们还被应用于新兴领域，如机器学习和大数据分析。例如，排序算法在处理大规模数据集的分布式计算中扮演了关键角色。在这些应用中，高效的排序算法能够显著减少计算时间，加速数据处理过程。

graph TD
A[数据规模和排序算法选择] -->|小规模数据| B[冒泡排序/插入排序]
A -->|大规模数据| C[快速排序/归并排序]
B --> D[易于实现]
C --> E[效率高]
D --> F[空间复杂度低]
E --> G[稳定排序]
F --> H[时间复杂度高]
G --> I[适合大规模数据]
H --> J[时间复杂度O(n^2)]
I --> K[空间复杂度O(n)]
J --> L[可用于部分有序数据]
K --> M[可用于稳定排序需求]
L --> N[选择建议]
M --> O[实现复杂度低]
N -->|总结| P[根据数据特性和需求选择]
O --> P

这个流程图简单总结了不同数据规模下的排序算法选择，以及相关的考虑因素和建议。选择正确的排序算法对于优化程序性能至关重要，因此，开发者必须根据实际问题来权衡各种因素，选择最适合的排序策略。