揭秘STM32模糊控制原理：深入浅出，一文看懂模糊控制奥秘

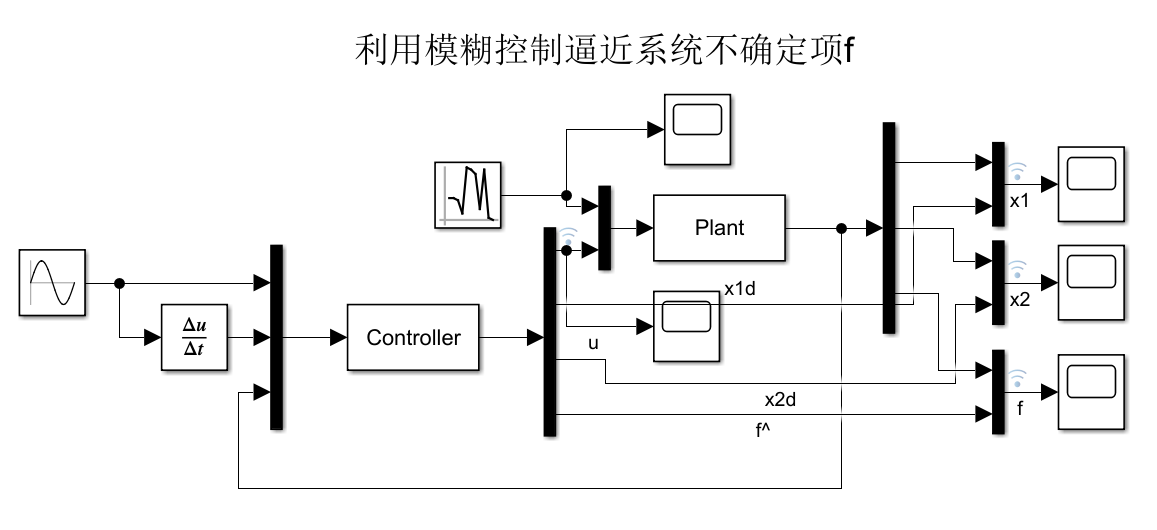
# 1. 模糊控制简介**

模糊控制是一种基于模糊逻辑的控制方法，它允许使用模糊语言（如“大”、“小”、“热”、“冷”）来描述系统行为和控制策略。与传统控制方法不同，模糊控制无需精确的数学模型，而是依赖于专家知识和经验。

模糊控制的主要思想是将系统输入和输出变量模糊化，即用模糊集合来表示。模糊集合是一种特殊的集合，其元素的隶属度介于0和1之间，表示元素属于该集合的程度。通过模糊推理，模糊控制系统可以根据模糊输入生成模糊输出，从而实现对系统的控制。

# 2. 模糊控制理论

### 2.1 模糊集理论

#### 2.1.1 模糊集合的定义和特性

模糊集合是经典集合理论的扩展，它允许集合的元素具有不同程度的隶属度。模糊集合由一个基本域（Universe of Discourse，UOD）和一个隶属度函数（Membership Function，MF）组成。隶属度函数将基本域中的每个元素映射到一个介于 0 到 1 之间的实数，表示该元素属于模糊集合的程度。

**定义：**

设 UOD 为一个非空集合，模糊集合 A 在 UOD 上定义为：

A = {(x, μA(x)) | x ∈ UOD}

其中：

* x 是 UOD 中的元素
* μA(x) 是 x 对模糊集合 A 的隶属度，且 0 ≤ μA(x) ≤ 1

**特性：**

* **非空性：**模糊集合至少包含一个元素，即存在 x ∈ UOD，使得 μA(x) > 0。
* **包含性：**对于 UOD 中的任何元素 x，其隶属度 μA(x) 介于 0 到 1 之间。
* **凸性：**对于 UOD 中的任何元素 x 和 y，以及 0 ≤ α ≤ 1，有：

μA(αx + (1 - α)y) ≥ min(μA(x), μA(y))

### 2.1.2 模糊集合的运算

模糊集合的运算与经典集合的运算类似，但由于隶属度函数的存在，运算结果也具有模糊性。

**并运算（Union）：**

(A ∪ B)(x) = max(μA(x), μB(x))

**交运算（Intersection）：**

(A ∩ B)(x) = min(μA(x), μB(x))

**补运算（Complement）：**

Ā(x) = 1 - μA(x)

**其他运算：**

* **代数和（Algebraic Sum）：**

(A + B)(x) = μA(x) + μB(x) - μA(x)μB(x)

* **代数积（Algebraic Product）：**

(A × B)(x) = μA(x)μB(x)

### 2.2 模糊规则推理

模糊规则推理是模糊控制的核心，它根据模糊规则库和输入变量的模糊值，推导出输出变量的模糊值。

#### 2.2.1 模糊推理机的结构

模糊推理机由以下部分组成：

* **模糊化器：**将输入变量的实际值转换为模糊值。
* **规则库：**包含一系列模糊规则，每个规则由一个前提部分和一个结论部分组成。
* **推理引擎：**根据规则库和输入变量的模糊值，推导出输出变量的模糊值。
* **反模糊化器：**将输出变量的模糊值转换为实际值。

#### 2.2.2 模糊推理方法

模糊推理方法有多种，常用的方法有：

* **Mamdani 方法：**

规则 i：如果 x 是 A 并且 y 是 B，那么 z 是 C

推理过程：

1. 将输入变量 x 和 y 模糊化，得到模糊值 μA(x) 和 μB(y)。
2. 计算每个规则的前提部分的真值，得到模糊值 μi = min(μA(x), μB(y))。
3. 根据每个规则的真值和结论部分，计算输出变量 z 的模糊值 μC(z)。
4. 将所有规则的输出模糊值聚合，得到最终的输出模糊值 μz(z)。
5. 将输出模糊值反模糊化，得到输出变量 z 的实际值。

* **Sugeno 方法：**

规则 i：如果 x 是 A 并且 y 是 B，那么 z = f(x, y)

推理过程：

1. 将输入变量 x 和 y 模糊化，得到模糊值 μA(x) 和 μB(y)。
2. 计算每个规则的前提部分的真值，得到模糊值 μi = min(μA(x), μB(y))。
3. 根据每个规则的真值和结论部分，计算输出变量 z 的实际值 z = f(x, y)。
4. 将所有规则的输出值聚合，得到最终的输出值 z。

# 3. STM32模糊控制实践

### 3.1 STM32模糊控制器开发环境

#### 3.1.1 开发工具介绍

STM32模糊控制器开发环境主要包括以下工具：

* **STM32CubeIDE：**一个集成的开发环境（IDE），用于编写、编译和调试STM32微控制器代码。
* **STM32CubeMX：**一个图形化配置工具，用于生成STM32微控制器外设的初始化代码。
* **STM32CubeF4：**一个STM32F4系列微控制器的硬件抽象层（HAL）库。
* **STM32CubeF7：**一个STM32F7系列微控制器的HAL库。

#### 3.1.2 模糊控制库介绍

STM32模糊控制库是专门针对STM32微控制器设计的模糊控制库。它提供了一组函数和宏，用于实现模糊控制算法。模糊控制库的主要组件包括：

* **模糊化模块：**将输入变量转换为模糊集合。
* **规则推理模块：**根据模糊规则对模糊集合进行推理。
* **反模糊化模块：**将推理结果转换为输出变量。

### 3.2 模糊控制算法实现

#### 3.2.1 模糊化

模糊化是将输入变量转换为模糊集合的过程。在STM32模糊控制库中，模糊化模块使用三角形隶属函数或梯形隶属函数。三角形隶属函数的定义如下：

μ(x) = max(0, min((x - a) / (b - a), (c - x) / (c - b)))

其中，a、b、c是三角形隶属函数的三个参数。

梯形隶属函数的定义如下：

μ(x) = max(0, min((x - a) / (b - a), 1, (c - x) / (c - d)))

其中，a、b、c、d是梯形隶属函数的四个参数。

#### 3.2.2 规则推理

规则推理是根据模糊规则对模糊集合进行推理的过程。在STM32模糊控制库中，规则推理模块使用Mamdani推理方法。Mamdani推理方法的步骤如下：

1. 对于每个输入变量，计算其隶属于每个模糊集合的程度。
2. 对于每个规则，计算其前提部分的真值。
3. 对于每个规则，计算其结论部分的真值。
4. 将所有规则的结论部分的真值聚合在一起。
5. 对聚合后的真值进行反模糊化。

#### 3.2.3 反模糊化

反模糊化是将推理结果转换为输出变量的过程。在STM32模糊控制库中，反模糊化模块使用重心法。重心法的定义如下：

y = (∑(μ(x) * x)) / (∑μ(x))

其中，μ(x)是输出变量的隶属函数，x是输出变量的值。

# 4. STM32模糊控制应用

### 4.1 电机速度控制

#### 4.1.1 速度控制系统设计

电机速度控制系统是一个典型的闭环控制系统，其目的是通过调节电机的输入电压或电流来控制电机的速度。模糊控制在电机速度控制中具有良好的应用前景，因为它可以处理非线性和不确定性因素。

电机速度控制系统主要包括以下几个部分：

- **速度传感器：**用于测量电机的实际速度。
- **模糊控制器：**根据速度传感器采集到的数据，输出控制信号。
- **功率驱动器：**根据模糊控制器的输出信号，调节电机的输入电压或电流。
- **电机：**将电能转换为机械能，驱动负载旋转。

#### 4.1.2 模糊控制器的设计与实现

电机速度控制的模糊控制器设计主要包括以下步骤：

1. **确定输入和输出变量：**通常，输入变量为速度误差和误差变化率，输出变量为控制量。
2. **定义模糊集：**根据输入和输出变量的取值范围，定义模糊集。例如，速度误差可以分为“负大”、“负中”、“负小”、“零”、“正小”、“正中”、“正大”等模糊集。
3. **建立模糊规则：**根据专家的经验或系统模型，建立模糊规则。例如，“如果速度误差为负大，并且误差变化率为负大，那么控制量为正大”。
4. **模糊化：**将速度误差和误差变化率的实际值映射到对应的模糊集。
5. **规则推理：**根据模糊规则，计算每个规则的输出。
6. **反模糊化：**将规则推理的结果映射到控制量的实际值。

### 4.2 温度控制

#### 4.2.1 温度控制系统设计

温度控制系统是一个典型的过程控制系统，其目的是通过调节加热或冷却设备的输入能量来控制系统的温度。模糊控制在温度控制中具有良好的应用前景，因为它可以处理非线性、时变和不确定性因素。

温度控制系统主要包括以下几个部分：

- **温度传感器：**用于测量系统的实际温度。
- **模糊控制器：**根据温度传感器采集到的数据，输出控制信号。
- **执行器：**根据模糊控制器的输出信号，调节加热或冷却设备的输入能量。
- **被控对象：**需要控制温度的系统或设备。

#### 4.2.2 模糊控制器的设计与实现

温度控制的模糊控制器设计主要包括以下步骤：

1. **确定输入和输出变量：**通常，输入变量为温度误差和误差变化率，输出变量为控制量。
2. **定义模糊集：**根据输入和输出变量的取值范围，定义模糊集。例如，温度误差可以分为“负大”、“负中”、“负小”、“零”、“正小”、“正中”、“正大”等模糊集。
3. **建立模糊规则：**根据专家的经验或系统模型，建立模糊规则。例如，“如果温度误差为负大，并且误差变化率为负大，那么控制量为正大”。
4. **模糊化：**将温度误差和误差变化率的实际值映射到对应的模糊集。
5. **规则推理：**根据模糊规则，计算每个规则的输出。
6. **反模糊化：**将规则推理的结果映射到控制量的实际值。

# 5. STM32模糊控制优化**

**5.1 模糊控制器的参数优化**

**5.1.1 参数优化方法**

模糊控制器的性能受其参数的影响，包括模糊集的隶属度函数、模糊规则和推理机制。参数优化旨在寻找一组最优参数，以提高模糊控制器的性能。常用的参数优化方法包括：

- **梯度下降法：**一种迭代算法，通过计算参数梯度并沿着梯度方向更新参数，逐步逼近最优值。
- **粒子群优化算法：**一种启发式算法，模拟粒子群的运动行为，通过粒子间的相互作用寻找最优解。
- **遗传算法：**一种启发式算法，模拟生物进化过程，通过选择、交叉和变异等操作产生新的解，逐步逼近最优值。

**5.1.2 优化策略**

参数优化策略根据具体应用和性能要求而定。常见的策略包括：

- **最小化误差：**优化参数以最小化模糊控制器输出与期望输出之间的误差。
- **最大化稳定性：**优化参数以提高模糊控制器的稳定性，避免系统振荡或发散。
- **综合优化：**综合考虑误差和稳定性等多重性能指标，优化参数以达到最佳平衡。

**5.2 模糊控制器的性能评估**

**5.2.1 性能指标**

模糊控制器的性能可以通过以下指标评估：

- **均方误差（MSE）：**衡量模糊控制器输出与期望输出之间的平均误差。
- **最大绝对误差（MAE）：**衡量模糊控制器输出与期望输出之间最大的绝对误差。
- **稳定性：**衡量模糊控制器是否能够保持系统稳定，避免振荡或发散。
- **鲁棒性：**衡量模糊控制器对系统扰动和参数变化的适应能力。

**5.2.2 评估方法**

模糊控制器的性能评估可以通过以下方法进行：

- **仿真：**使用仿真模型对模糊控制器进行评估，分析其在不同输入和扰动下的性能。
- **实验：**在实际系统中部署模糊控制器，收集实际数据并评估其性能。
- **对比分析：**将模糊控制器与其他控制方法（如PID控制）进行对比，分析其优缺点。