【PCA在模式识别中的应用】：揭秘如何利用PCA区分Iris物种（实战案例）

目录
摘要
关键字
1. PCA在模式识别中的理论基础

1.1 数据的多维性和相关性
1.2 降维的数学表达

2. PCA降维技术详解

2.1 主成分分析的基本原理

2.1.1 数据的协方差矩阵
2.1.2 特征值和特征向量的数学解释

2.2 PCA算法的数学推导

2.2.1 数据标准化处理
2.2.2 主成分的提取方法
2.2.3 保留关键信息的技巧

2.3 PCA降维的实际影响

2.3.1 维度灾难的解释
2.3.2 数据可视化与降维

解锁专栏，查看完整目录
摘要
主成分分析（PCA）作为一种经典的降维技术，在模式识别领域具有重要的理论和应用价值。本文首先介绍了PCA的理论基础，并详细解读了其数学原理，包括数据的协方差矩阵、特征值和特征向量等关键概念。接着，本文深入分析了PCA降维技术，并探讨了如何通过数据标准化、主成分提取等步骤实现有效降维，以及降维对维度灾难的解决和数据可视化的影响。以Iris数据集为例，本文展示了PCA在物种识别中的应用，包括特征降维、构建分类器并评估分类准确率。最后，本文探讨了PCA技术在大数据环境下的挑战和未来发展方向，包括与其他降维技术的比较和PCA优化的可能途径。通过对PCA的理论和实践案例分析，本文旨在为模式识别领域的研究者提供深入的理解和启示。
关键字
主成分分析；模式识别；降维技术；数据标准化；特征提取；分类准确率
参考资源链接：Fisher Iris Setosa数据的主成分分析及可视化- Matlab实现
1. PCA在模式识别中的理论基础
在模式识别领域，主成分分析（PCA）作为一种经典的数据降维技术，广泛应用于提高数据处理效率和系统性能。PCA通过正交变换将可能相关的变量转换为一系列线性不相关的变量，称为主成分。这些主成分被构造为数据方差的递减顺序排列，目的是将原始数据转换到一个新的坐标系统中，使得数据的前几个主成分尽可能多地包含原始数据的信息。
1.1 数据的多维性和相关性
在高维空间中，数据点的分布特征可能由于维度的诅咒而变得难以捉摸。相关性分析揭示变量之间的线性关系，而PCA在识别和利用这些相关性方面具有独特的优势，能够通过降维减少噪声和冗余信息，同时保留数据最重要的结构。
1.2 降维的数学表达
PCA的数学模型基于协方差矩阵的特征分解，其核心思想是寻找能够最大程度保留数据方差的方向。在数学上，这等同于求解数据协方差矩阵的特征值和特征向量，其中特征值表示对应的特征向量方向上的数据方差大小，特征向量则定义了新的坐标轴。
% 假设数据矩阵X，其中每一行代表一个样本，每一列代表一个特征X = [...] % 数据矩阵% 计算数据矩阵的协方差矩阵cov_matrix = Covariance[X]% 计算协方差矩阵的特征值和特征向量[values, vectors] = Eigensystem[cov_matrix]
在上述公式中，Covariance、Eigensystem 分别为计算协方差矩阵和获取特征值及特征向量的函数。特征值从大到小排序，并与特征向量一一对应，主成分按照特征值的大小顺序排列，代表了数据在不同方向上的方差。
2. PCA降维技术详解
2.1 主成分分析的基本原理
2.1.1 数据的协方差矩阵
协方差矩阵是理解主成分分析（PCA）的基础。它用于衡量数据集中各变量间的总体相关性。假设有一个随机变量的向量 (X = [X_1, X_2, …, X_n])，其协方差矩阵 (C) 可以表示为：
[ C = \begin{bmatrix}
cov(X_1, X_1) & cov(X_1, X_2) & \dots & cov(X_1, X_n) \
cov(X_2, X_1) & cov(X_2, X_2) & \dots & cov(X_2, X_n) \
\vdots & \vdots & \ddots & \vdots \
cov(X_n, X_1) & cov(X_n, X_2) & \dots & cov(X_n, X_n) \
\end{bmatrix} ]
其中 (cov(X_i, X_j)) 表示变量 (X_i) 和 (X_j) 的协方差。协方差矩阵是一个对称矩阵，其对角线元素表示各个变量的方差，非对角线元素表示变量之间的协方差。
2.1.2 特征值和特征向量的数学解释
特征值和特征向量是线性代数中的基本概念，它们在线性变换中起着重要作用。在PCA中，特征值和特征向量用于确定数据变换的方向和幅度。

特征值（Eigenvalues）：对于一个 (n \times n) 的矩阵 (A)，如果存在一个非零向量 (v) 和一个标量 (\lambda)，使得 (Av = \lambda v)，则 (\lambda) 称为矩阵 (A) 的一个特征值，而 (v) 称为对应的特征向量。
特征向量（Eigenvectors）：与一个特征值相对应的非零向量。

在PCA的上下文中，数据协方差矩阵的特征向量确定了数据的主成分方向，而相应的特征值表明了在这些方向上数据的方差大小。特征值越大，对应的主成分解释的数据变异性越多。
2.2 PCA算法的数学推导
2.2.1 数据标准化处理
由于PCA对数据的尺度很敏感，不同量级的数据会影响分析结果，因此通常在进行PCA之前需要对数据进行标准化处理。标准化处理的目的是让每个特征的均值为0，标准差为1。对于每个特征 (X_i)，标准化的过程如下：
[ X’_i = \frac{X_i - \mu_i}{\sigma_i} ]
其中，(X’_i) 是标准化后的特征，(X_i) 是原始特征，(\mu_i) 和 (\sigma_i) 分别是 (X_i) 的均值和标准差。
2.2.2 主成分的提取方法
提取主成分的过程就是找到一组正交基，这组基可以捕捉数据的绝大部分方差。在数学上，这等价于对协方差矩阵 (C) 进行特征分解，得到特征值和特征向量。对于标准化后的数据 (X’)，求解特征方程：
[ \text{det}(C - \lambda I) = 0 ]
解出特征值 (\lambda_i) 和对应的特征向量 (v_i)。这些特征向量就是数据的主成分方向，而特征值表示沿着这些方向数据的方差大小。
2.2.3 保留关键信息的技巧
由于数据可能具有多个维度，全部使用这些主成分会导致计算量大且复杂。为了简化模型，通常会选择前几个最重要的主成分，即那些具有较大特征值的特征向量。一个常用的选择策略是保留95%或99%的总方差。这意味着只选择那些特征值总和占总特征值和的比例达到或超过目标百分比的主成分。
例如，如果数据集有10个特征，而前3个特征值加起来占总特征值和的90%，那么就可以只保留这3个主成分以简化数据结构。
2.3 PCA降维的实际影响
2.3.1 维度灾难的解释
在数据分析中，随着特征数量的增加，数据的维度也随之增加。这可能导致所谓的“维度灾难”，即数据在高维空间中变得稀疏，数据点之间的距离变得相似，因此很难找到有意义的模式。PCA通过将数据投影到少数几个主成分上，可以有效地减少维度，缓解维度灾难。
2.3.2 数据可视化与降维
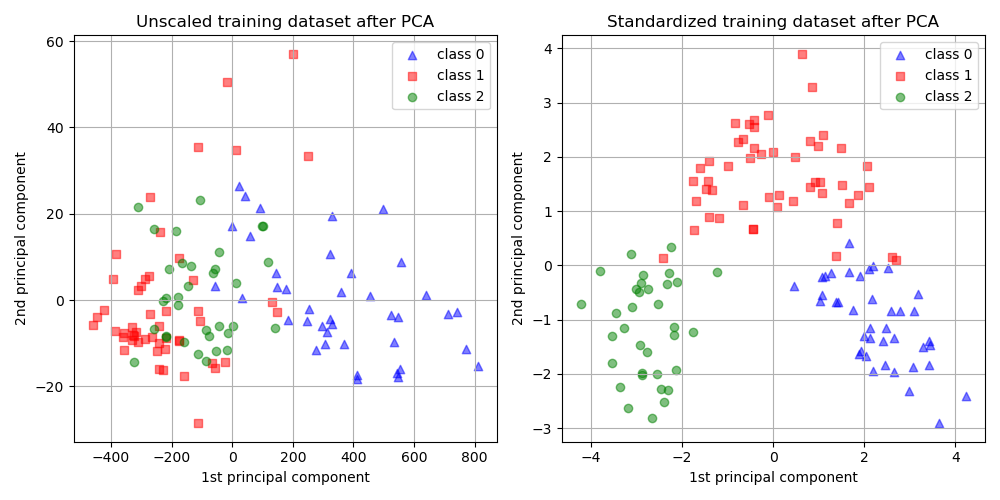
可视化是数据分析中一个重要的方面。由于我们无法直观地看到超过三维的数据，因此在进行数据分析前通常需要降维。PCA使我们能够将高维数据转换到二维或三维空间进行可视化，以便更容易识别数据中的趋势和模式。例如，一个复杂的多维数据集可能在二维PCA投影中表现出明显的聚类，这有助于我们理解和解释数据。
以上内容对PCA降维技术进行了详细的技术性讲解，并对降维技术如何解决高维数据问题进行了深入探讨。在下一章节中，我们将通过一个实际的数据集—Iris数据集，深入探讨PCA在