【Python编程起步】：单链表反转算法，从入门到精通

# 1. 单链表数据结构基础

单链表是一种基础且重要的数据结构，它在IT行业中的应用广泛，特别是在复杂系统和算法的设计中。简单来说，单链表由一系列节点组成，每个节点都包含数据和指向下一个节点的指针。在这一章节中，我们将从最简单的定义开始，逐步了解单链表的结构，并探讨如何实现基本的链表操作。我们会讨论如何添加、删除和访问链表中的元素，这为后续章节中讨论更复杂的主题，如单链表的反转，打下坚实的基础。通过本章的学习，读者将对单链表有一个全面的认识，并能够理解其作为其他数据结构基础的重要性。

# 2. 单链表反转理论基础

## 2.1 链表的概念和结构
### 2.1.1 链表节点的定义
在计算机科学中，链表是一种常见的基础数据结构，它由一系列节点组成，每个节点包含数据部分以及指向下一个节点的指针。在单链表中，节点的指针仅指向一个方向，即下一个节点，因此称为“单链表”。

为了更好地理解链表，我们需要定义一个链表节点的数据结构。在Python中，这通常通过类来实现。以下是一个简单的单链表节点类的实现：

class ListNode:
    def __init__(self, value=0, next=None):
        self.value = value
        self.next = next

在这段代码中，`ListNode`类有两个属性：`value`和`next`。`value`代表节点存储的数据，而`next`是一个指向下一个`ListNode`对象的指针。这样的设计使得链表可以灵活地存储数据，并且能够动态地增长或缩短。

### 2.1.2 链表类型及其特点
链表有多种类型，根据节点间连接方式的不同，主要分为单链表、双链表和循环链表。单链表的特点是每个节点仅指向一个方向，即下一个节点。而双链表的每个节点会指向两个方向，即下一个节点和上一个节点。循环链表则是链表的尾部节点的指针指向头部节点，形成一个环。

每种链表类型都有其特定的使用场景，但在本节中我们重点探讨单链表，这是因为单链表是链表类型中最基本、最简单的一种。单链表的操作主要包括插入、删除、搜索和反转等。

## 2.2 反转算法的理论基础
### 2.2.1 算法的时间复杂度和空间复杂度
在探讨单链表反转算法之前，了解算法的时间复杂度和空间复杂度是非常重要的。时间复杂度描述了算法执行所需要的时间量，通常用大O表示法表示。空间复杂度描述了算法执行所需要的额外空间量。

单链表反转算法的时间复杂度为O(n)，其中n是链表的长度。这是因为在反转过程中，每个节点的指针方向都会被改变一次。反转算法的空间复杂度为O(1)，因为除了输出的反转链表外，并不需要额外的存储空间。

### 2.2.2 反转算法的逻辑理解
链表反转的逻辑可以通过模拟一个“手”通过链表从头到尾移动的过程来理解。想象一下你左手持链表头节点，右手持链表尾节点，然后通过一系列的步骤交换左右手所持节点的位置，最终达到反转链表的目的。

在算法层面，我们通过迭代的方法，从链表的头节点开始，逐个遍历节点，然后改变每个节点的指针方向，使其指向前一个节点。通过这种方式，我们逐步构建出一个反转后的链表。

## 2.3 单链表反转的数学原理
### 2.3.1 指针操作的数学解释
链表操作中的指针实际上可以看作是一种数学上的映射。单链表的节点可以看作是一组有序对，即节点值和指向下一个节点的指针。当我们执行反转操作时，实际上是在对这些有序对进行一一映射，将它们转换成新的有序对。

数学上，这种映射可以表示为：

f(当前节点) = 原来的下一个节点
f(原来的下一个节点) = 当前节点

这样定义的映射具有可逆性，是链表反转能够成功实现的关键。

### 2.3.2 算法推导过程
单链表反转算法的推导过程可以分为以下步骤：
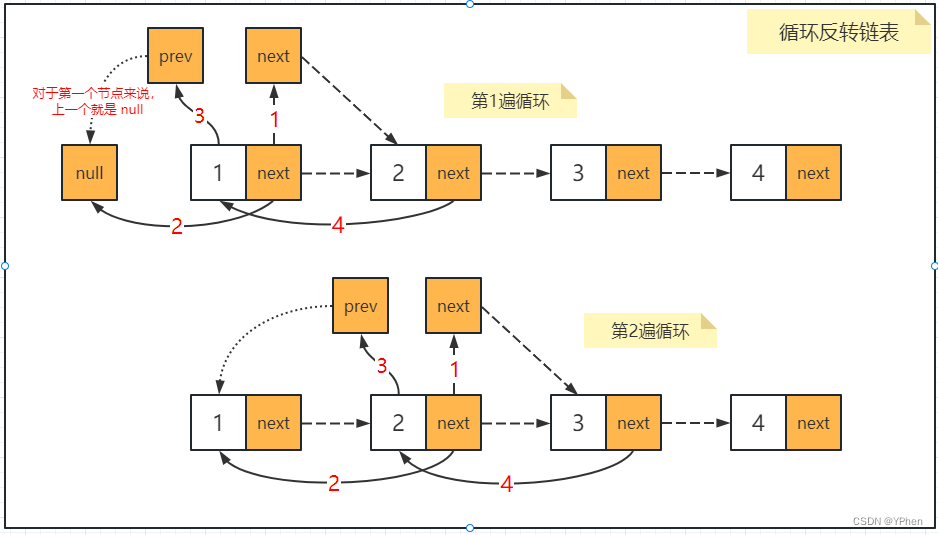
1. 初始化三个指针变量，`prev`、`current`和`next`。`prev`初始为None，`current`为链表头节点，`next`为None。
2. 遍历链表，对于每个节点，先保存其下一个节点，即`next = current.next`。
3. 改变当前节点的指针方向，使其指向前一个节点，即`current.next = prev`。
4. 将`prev`和`current`分别前移一位，即`prev = current`和`current = next`。
5. 重复步骤2至4，直到`current`为None，此时`prev`即为新的头节点，也就是反转后的链表。

通过以上步骤，我们可以得到反转后的链表。这个过程不仅可以用伪代码描述，还可以用实际的编程语言实现。以下是Python语言实现的单链表反转算法：

def reverse_linked_list(head):
    prev = None
    current = head
    while current is not None:
        next = current.next  # 保存当前节点的下一个节点
        current.next = prev  # 改变当前节点的指针方向
        prev = current       # 移动prev和current
        current = next
    return prev

在这段代码中，我们使用了一个循环结构来执行上述的步骤，直到遍历完所有的节点，返回新的头节点`prev`。这段代码的逻辑清晰，体现了链表反转算法的核心思想。

# 3. 单链表反转的Python实现

单链表是数据结构学习中的经典话题，而反转链表是检验程序员对链表操作理解程度的重要关卡。本章节将详细探讨如何使用Python语言来实现单链表的反转。我们将从基础代码实现入手，逐步探索优化技巧，并在最后讨论如何处理Python中可能出现的反转算法错误。

## 3.1 单链表反转的基础代码实现

### 3.1.1 链表节点类的定义

在Python中，单链表由一系列节点组成，每个节点是一个对象，包含数据部分和指向下一个节点的指针。首先，我们定义一个节点类Node，包含数据值和指向下一个节点的引用。

class Node:
    def __init__(self, value):
        self.value = value
        self.next = None

逻辑分析与参数说明：Node类的构造函数接受一个参数`value`，用于初始化节点存储的数据值。`next`属性被初始化为`None`，表示该节点的下一个节点为空。

### 3.1.2 反转函数的编写

接下来，我们编写一个反转单链表的函数`reverse_linked_list`。该函数的输入为链表的头节点，输出为反转后的链表的头节点。

def reverse_linked_list(head):
    prev = None
    current = head
    while current is not None:
        next_temp = current.next  # 保存当前节点的下一个节点
        current.next = prev       # 将当前节点指向前一个节点
        prev = current            # 前一个节点后移
        current = next_temp       # 当前节点后移
    return prev

代码逻辑分析：该函数中使用三个指针，`prev`、`current`和`next_temp`。初始时，`prev`为`None`，表示反转后的链表还没有开始；`current`为链表的头节点。在while循环中，我们首先保存`current`节点的下一个节点到`next_temp`，然后将`current.next`设置为`prev`，完成当前节点的反转操作；之后，`prev`和`current`指针都向后移动一位。循环继续，直到`current`指针为空，此时`prev`指向新的头节点，函数返回这个节点。

### 3.1.3 代码块的逻辑解读

上述代码是一个基本的单链表反转实现，但是它的逻辑并不复杂。首先，初始化三个指针`prev`、`current`和`next_temp`，`prev`用于记录已经反转的链表的最后一个节点，`current`用于遍历原链表，`next_temp`用于临时保存`current`的下一个节点。

具体步骤如下：
1. 初始时，`prev`为`None`，`current`为头节点。
2. 循环开始，首先保存`current.next`到`next_temp`。
3. 然后将`current.next`指向`prev`，将`current`之前遍历的链表连接到反转的链表上。
4. 接着`prev`移动到`current`的位置，`current`也向后移动一个节点。
5. 当`current`为空时，说明遍历到原链表的尾部，此时`prev`是反转后链表的头节点。
6. 最终返回`prev`，即为新的头节点。

该实现的时间复杂度为O(n)，空间复杂度为O(1)，因为它只使用了有限的几个指针变量，没有额外分配存储空间。

## 3.2 反转算法的优化技巧

### 3.2.1 递归方法的优化

除了迭代的方法外，也可以使用递归方法来实现单链表的反转。递归方法通过递归调用自身完成链表的反转，但它在处理很长的链表时可能会遇到栈溢出的问题。

递归实现的代码如下：

def reverse_linked_list_recursive(head):
    if head is None or head.next is None:
        return head
    reversed_head = reverse_linked_list_recursive(head.next)
    head.next.next = head
    head.next = None
    return reversed_head

逻辑分析与参数说明：递归函数`reverse_linked_list_recursive`首先检查当前节点是否为空或者是否是尾节点，如果是，直接返回该节点。然后，函数递归调用自身处理当前节点的下一个节点，并将当前节点移动到新链表的尾部。需要注意的是，在反转之后，要将原链表中当前节点的下一个节点的`next`指针设置为当前节点，并将当前节点的`next`指针设置为`None`。

尽管递归方法在编写上简洁易懂，但在深度递归的情况下，可能会导致栈溢出。因此，在实现时需注意递归深度限制，并在可能的情况下使用迭代方法。

### 3.2.2 迭代方法的优化

迭代方法是更常用且通常更高效的反转链表方式。在迭代过程中，我们通过三个指针（`prev`、`current`、`next_temp`）来完成操作，如前面所介绍。

优化迭代方法通常涉及到减少不必要的变量操作或使代码更加清晰易懂。例如，可以将`current`和`prev`的赋值合并到一行中，减少代码行数，提高可读性。

一个优化后的迭代实现如下：

def reverse_linked_list_optimized(head):
    prev, current = None, head
    while current:
        current.next, prev, current = prev, current, current.next
    return prev

逻辑分析与参数说明：在这个优化后的版本中，我们通过将赋值语句进行打包，使用Python的多重赋值特性，可以在一行代码内完成三个指针的更新。当`current`非空时，`current.next`被设置为`prev`（完成反转），`prev`更新为`current`的位置，`current`移动到下一个节点。这个过程将一直持续到`current`为空，此时`prev`即为反转后链表的新头部。

使用上述优化后的迭代方法，可以实现与之前相同功能的同时，减少代码量，提高代码的执行效率。

## 3.3 Python中反转算法的错误处理

### 3.3.1 常见错误类型及原因

在Python中实现单链表反转的过程中，开发者可能会遇到多种类型的错误。以下是一些常见的错误类型及其原因：

1. 空链表错误（如尝试反转一个空链表）。
2. 循环链表错误（链表尾节点的`next`指针指向了头节点或其他非`None`的节点）。
3. 边界条件处理不当（未正确处理边界情况，如链表只有一个节点时的特殊情况）。
4. 原始数据破坏（在反转过程中，错误地修改了原始链表中的节点结构）。

### 3.3.2 错误处理的最佳实践

为了避免上述错误的发生，建议遵循一些最佳实践：

1. 在实现链表操作时，总是检查链表是否为空，如果是，可以提前返回一个明确的结果，如`None`。
2. 当处理链表尾部节点时，确保将该节点的`next`指针设置为`None`，避免形成循环链表。
3. 使用辅助函数来处理边界条件，例如，创建一个辅助函数来反转一个节点，然后再在主函数中调用它，可以清晰地处理边界情况。
4. 使用断言（`assert`）来检查链表的结构是否在操作过程中被破坏，例如，在反转前后的链表中检查每个节点的`next`指针是否正确。

def assert_linked_list_integrity(head):
    current = head
    prev = None
    while current:
        assert current.next != head, "Detected a loop in the list"
        assert current.next != prev, "The linked list is not well-formed"
        prev = current
        current = current.next

在实际的开发中，我们应当使用断言来确保链表的完整性和正确性，尤其是在调试阶段。

综上所述，本章节详细阐述了使用Python实现单链表反转的基本方法，并提供了优化技巧和错误处理的最佳实践。通过这些方法和技巧，开发者可以高效准确地编写出健壮的单链表反转算法。接下来，我们将进入第四章，探讨单链表反转算法的应用与实战。

# 4. 单链表反转算法的应用与实战

在本章节中，我们将深入探讨单链表反转算法在实际项目中的应用，并通过扩展应用来加深对其概念的理解。最后，我们将实战演练，构建一个链表反转项目，通过需求分析、设计、功能实现到测试的全过程来加深理解。

## 4.1 反转算法在实际项目中的应用

单链表反转算法在实际项目中的应用十分广泛。理解反转算法及其应用，对于任何数据结构和算法的学习者来说，都是至关重要的。

### 4.1.1 链表操作在数据结构中的地位

链表是一种基础的数据结构，其节点通过指针或引用连接，形成序列。与数组不同，链表的节点可以在内存中任何位置，使得插入和删除操作更加高效。反转链表是链表操作中的一个基本技能，它通过改变节点之间的指针关系来实现整个链表的翻转。

在数据结构的多个应用场景中，例如在操作系统中管理内存碎片，以及在数据库中处理记录链，链表反转均扮演了重要角色。掌握反转算法，能够帮助开发人员更好地理解和运用链表这一数据结构。

### 4.1.2 反转算法的具体应用场景

反转链表的应用可以细分为多种情形：

1. **逆序输出**：有时候我们需要从链表的尾部开始输出元素，如打印链表内容。
2. **链表分割**：在处理某些复杂问题时，可能需要将链表分割成两部分，反转其中的一部分可以提供更直观的视图。
3. **后续操作**：在特定的算法或数据操作中，如平衡二叉树的中序遍历到后序遍历的转换，反转链表是关键步骤之一。

## 4.2 单链表反转算法的扩展应用

链表反转算法具有极高的可扩展性，它不仅可以应用于单链表，还能通过修改来适应其他类型的链表结构。

### 4.2.1 双链表及多链表的反转

双链表与单链表类似，但每个节点都包含两个指针，分别指向前一个和后一个节点。多链表是更为复杂的结构，它允许一个节点指向多个后续节点。尽管数据结构变得更加复杂，反转算法的基本原理仍然适用。

对于双链表反转，除了要调整每个节点指向下一个节点的指针外，还需要调整其指向前一个节点的指针。对于多链表的反转，由于一个节点可能有多个后续节点，因此在反转过程中需要特别处理每个节点的指针。

### 4.2.2 链表反转与其他数据结构的结合

在一些特定的应用中，链表反转可以与其他数据结构结合使用。例如，在实现一个栈或队列时，可以使用链表作为其底层数据结构，并在其上实现反转操作。此外，链表反转还可以被用于实现某些特定的算法，如归并排序中的链表排序。

## 4.3 实战演练：构建链表反转项目

在实战演练中，我们将通过构建一个链表反转项目来加深对链表反转算法的理解。

### 4.3.1 需求分析与设计

**需求分析**：构建一个链表反转系统，该系统能够：

- 接收用户输入的链表序列；
- 提供反转链表的功能；
- 显示反转前后的链表序列；
- 测试反转算法的性能。

**系统设计**：系统主要包括以下几个模块：

- **链表节点类**：定义链表节点，包含节点数据和指向下一个节点的指针。
- **链表操作类**：提供链表的创建、添加节点、打印节点和反转链表的功能。
- **用户界面**：允许用户输入数据和接收系统反馈。
- **性能测试模块**：用于测试反转操作的性能，如时间和空间复杂度。

### 4.3.2 功能实现与测试

接下来，我们将以Python语言来实现上述设计的链表反转系统。

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class LinkedList:
    def __init__(self):
        self.head = None

    def append(self, val):
        if not self.head:
            self.head = ListNode(val)
        else:
            current = self.head
            while current.next:
                current = current.next
            current.next = ListNode(val)

    def reverse(self):
        prev, current = None, self.head
        while current:
            next_node = current.next
            current.next = prev
            prev = current
            current = next_node
        self.head = prev

    def display(self):
        current = self.head
        while current:
            print(current.val, end=" ")
            current = current.next
        print()

# 使用链表
my_list = LinkedList()
my_list.append(1)
my_list.append(2)
my_list.append(3)

print("Original List:")
my_list.display()

my_list.reverse()
print("Reversed List:")
my_list.display()

在上面的代码中，我们定义了`ListNode`类来表示链表节点，并创建了`LinkedList`类来管理链表操作。`LinkedList`类包含添加节点的`append`方法，反转链表的`reverse`方法以及打印链表的`display`方法。

通过运行上述代码，可以实现一个基础的链表反转操作。进一步，可以通过增加测试模块来对链表反转操作的性能进行评估，比如记录反转操作前后的执行时间。

以上部分实现了链表反转的核心功能，但完整的项目还需要包含用户界面和性能测试模块。用户界面可以采用命令行交互或图形界面来实现，性能测试模块可以使用标准库中的`time`模块来测量时间复杂度。

通过实战演练，我们不仅能够加深对链表反转算法的理解，还能学习如何将理论知识应用到实际开发中。

# 5. 单链表反转算法的深入研究

在深入探讨单链表反转算法之前，我们需要了解算法研究的广度和深度，以及它在其他领域的潜在应用。在本章中，我们将分析更高级的数据结构、并行计算技术，以及探索单链表反转算法的学术进展和创新。

## 5.1 反转算法的进阶探讨

### 5.1.1 高级数据结构与反转算法

当我们进入算法研究的进阶阶段，单链表反转已经不再是孤立的概念。它与其他高级数据结构如红黑树、AVL树、B树等有着千丝万缕的联系。在某些场景中，反转单链表可以看作是构建这些复杂数据结构的基石。

- **红黑树与链表反转**：红黑树在插入和删除节点时，可能需要进行颜色调整和树旋转操作。在特定条件下，树的旋转可以被视为链表的反转操作。理解单链表反转有助于掌握这些更复杂数据结构的操作机制。

- **AVL树平衡**：AVL树是一种高度平衡的二叉搜索树，其平衡的维护涉及到节点的多次旋转。链表的反转逻辑有助于理解节点平衡后结构的调整。

### 5.1.2 反转算法的并行计算与优化

在多核处理器和分布式计算的背景下，并行算法成为了研究热点。单链表反转算法的并行化可以显著提升大数据处理的效率。

- **并行反转的挑战**：链表节点间存在依赖关系，使得并行化变得困难。我们需要寻找算法中的独立计算部分，以实现并行处理。

- **并行策略**：一种可能的策略是将链表分割成多个部分，分别在不同的处理器或节点上进行反转，最后将各个部分的结果连接起来。

## 5.2 学术研究与算法创新

### 5.2.1 反转算法的最新研究成果

学术界对于链表反转的研究不断推进，新的算法和优化手段层出不穷。最新的研究成果可能涉及到如下几个方面：

- **理论突破**：通过数学建模和算法分析，研究者可能发现了更优的时间复杂度或空间复杂度的反转算法。

- **硬件优化**：利用硬件特性，如缓存优化、内存访问模式等，提升算法的执行效率。

### 5.2.2 算法创新与未来发展方向

随着技术的进步，算法创新是推动软件工程发展的核心力量。对于单链表反转算法，未来的创新可能会关注于：

- **自适应算法**：设计根据链表大小和节点分布自动调整算法策略的自适应反转算法。

- **跨平台应用**：开发能够在不同硬件架构和操作系统上高效运行的反转算法。

## 5.3 反转算法在其他编程语言中的实现

### 5.3.1 C/C++中的链表反转

C/C++是系统编程的主要语言，对于性能要求极高的场合，反转算法的C/C++实现将直接影响程序的运行效率。

typedef struct Node {
    int data;
    struct Node* next;
} Node;

Node* reverseList(Node* head) {
    Node* prev = NULL;
    Node* current = head;
    Node* next = NULL;
    while (current != NULL) {
        next = current->next;
        current->next = prev;
        prev = current;
        current = next;
    }
    head = prev;
    return head;
}

### 5.3.2 Java、C#等语言中的链表反转

Java和C#等语言提供了垃圾回收机制和丰富的类库支持，使得链表反转等基础操作更为便捷和安全。

public class LinkedList {
    Node head; // head of the list
    // Linked list Node
    static class Node {
        int data;
        Node next;
        Node(int d) {
            data = d;
            next = null;
        }
    }

    //反转链表
    Node reverseList(Node head) {
        Node prev = null;
        Node current = head;
        Node next = null;
        while (current != null) {
            next = current.next;
            current.next = prev;
            prev = current;
            current = next;
        }
        head = prev;
        return head;
    }
}

以上代码展示了在Java中实现的单链表反转方法。与C/C++相比，Java的代码更加简洁，得益于语言特性的支持，减少了内存管理的复杂性。