二阶系统时域分析：如何通过PID控制器实现联合设计优化


# 摘要
本文旨在提供对二阶系统时域分析及PID控制器设计的全面理解，并探讨联合设计优化策略及其实践应用。文章首先介绍了二阶系统时域分析的基础知识，随后深入解释了PID控制器的组成、功能及参数对系统性能的影响，并详细阐述了控制器的设计流程。在联合设计优化策略部分，本文讲解了优化方法以及如何通过系统仿真实验进行验证。通过案例分析，文章展示了特定二阶系统的设计实例和联合设计优化的实践过程，并对整个过程进行了总结和启示。最后，本文对研究成果进行了总结，并提出了当前研究的挑战以及未来的研究方向。
# 关键字
二阶系统；时域分析；PID控制器；参数优化；联合设计；仿真实验

参考资源链接：[二阶系统时域分析：性能指标与瞬态响应](https://wenku.csdn.net/doc/742te1qkcj?spm=1055.2635.3001.10343)
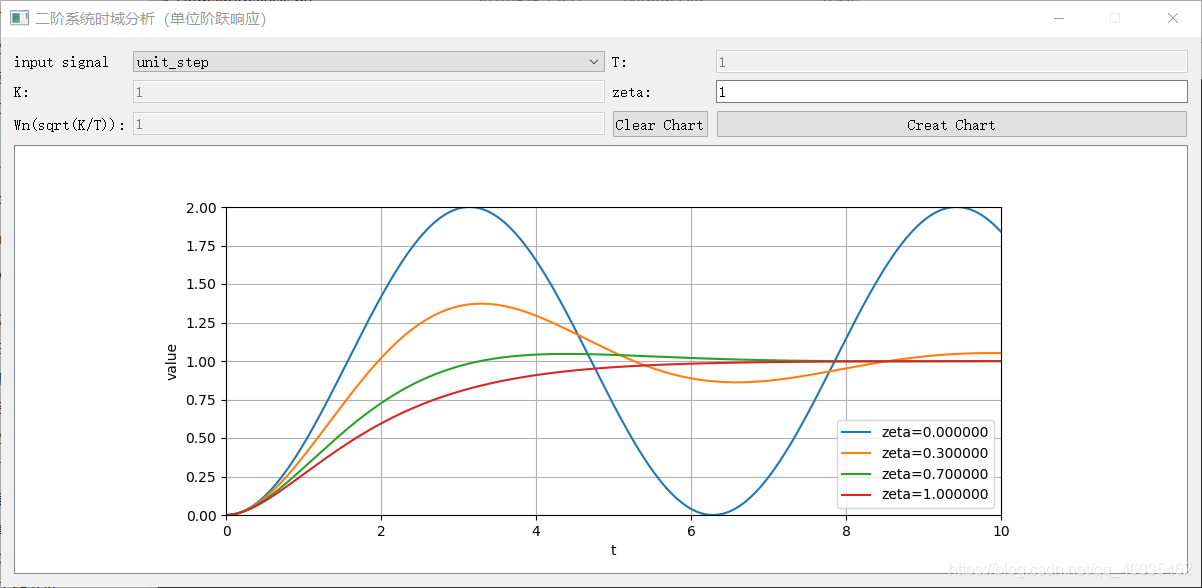
# 1. 二阶系统时域分析基础

## 1.1 二阶系统的定义与构成

二阶系统是控制系统分析中一个重要的基础模型。它通常由两个独立的能量存储元素（如弹簧和质量块）组成，并且能够表现出复杂的动态行为。在时域分析中，二阶系统的特性主要由阻尼比和自然频率两个参数决定。

## 1.2 时域分析的重要性

时域分析允许工程师直接观测系统的响应随时间的变化过程。通过绘制系统的单位阶跃响应或脉冲响应曲线，可以直观地评价系统的性能，如上升时间、超调量和稳态误差等。这些性能指标对于系统设计至关重要。

## 1.3 基本动态方程

二阶系统的动态方程通常以微分方程的形式给出，例如：

a2 * d^2y(t)/dt^2 + a1 * dy(t)/dt + a0 * y(t) = b0 * u(t)

其中，`y(t)`是输出，`u(t)`是输入，`a2`、`a1`、`a0`和`b0`是与系统特性相关的系数。通过求解这样的微分方程，可以得到系统的瞬态和稳态特性。

# 2. 理解PID控制器的原理

### PID控制器的组成与功能

#### 比例（P）、积分（I）、微分（D）的作用

比例-积分-微分（PID）控制器是一种常见的反馈回路控制器，广泛应用于工业控制系统中。PID控制器通过比较设定点与实际输出值的差异（即偏差），综合比例、积分和微分三种控制作用来调整控制输入，使系统输出响应跟随设定值。

- **比例（P）**：比例控制作用负责对偏差进行直接放大，根据偏差的大小来调整控制动作。比例增益越大，控制器的反应越敏感，输出调整也越快。但是，过大的比例增益会导致系统振荡，稳定性降低。

- **积分（I）**：积分控制作用负责消除稳态误差，即长期累积偏差对系统的影响。通过积分控制，系统能够在较长时间内逐渐消除偏差。然而，积分作用过强会导致系统响应速度变慢，甚至产生振荡。

- **微分（D）**：微分控制作用预测偏差的变化趋势，对偏差的变化率进行响应。微分控制可以提前对系统动态做出调整，以减少过冲和振荡。不过，如果微分增益设置不当，可能会放大噪声，增加系统的不稳定性。

#### PID控制器的基本方程

PID控制器的一般表达式可以表示为：

\[ u(t) = K_p e(t) + K_i \int_{0}^{t} e(\tau) d\tau + K_d \frac{de(t)}{dt} \]

其中，\( u(t) \)是控制器的输出，\( e(t) \)是偏差（即设定值与测量值之间的差），\( K_p \)、\( K_i \)和\( K_d \)分别是比例、积分和微分增益系数，\( t \)表示时间。

### PID参数对系统性能的影响

#### 参数调整的理论基础

PID参数的调整基于系统的动态响应，一般而言，控制系统的设计要求系统响应快速、稳定且无超调或最小超调。参数的调整通常遵循以下原则：

- **比例增益** \( K_p \)：比例增益负责控制系统响应的速度和幅度。增大 \( K_p \)可以加快响应速度，但若过大，则可能引起系统振荡。

- **积分增益** \( K_i \)：积分增益用来消除稳态误差。增加 \( K_i \)可以减少或消除稳态误差，但增加过快会导致系统响应变慢，甚至出现积分饱和或振荡。

- **微分增益** \( K_d \)：微分增益有助于提高系统的阻尼比，减少过冲和振荡。较大的 \( K_d \)可减小系统上升时间，但过大的 \( K_d \)会放大测量噪声，影响系统稳定性。

#### 实际系统的响应分析

在实际应用中，系统响应通常通过阶跃响应来分析，主要考虑以下几个性能指标：

- **上升时间**：输出从设定值的10%上升到90%所需要的时间。
- **峰值时间**：输出达到第一个峰值所需要的时间。
- **超调量**：输出峰值超过设定值的百分比。
- **调整时间**：输出进入并保持在设定值的±5%或±2%范围内所需的时间。
- **稳态误差**：系统输出长时间后与设定值之间的差异。

### PID控制器的设计流程

#### 控制器设计步骤概述

设计一个有效的PID控制器一般包括以下步骤：

1. **系统建模**：首先需要对控制对象进行数学建模，得到系统传递函数或状态空间表达式。
2. **确定控制目标**：根据系统性能要求，定义系统的性能指标。
3. **参数初始化**：根据经验或简单规则初始化PID参数。
4. **试错调整**：通过仿真或实际测试，观察系统响应并调整PID参数，以满足控制目标。
5. **稳定性分析**：进行稳定性分析，确保系统稳定运行。
6. **优化与微调**：根据实际响应结果进行微调，提高系统性能。

#### 设计中常见的问题及对策

在PID控制器的设计过程中，可能会遇到各种问题，常见问题及对策如下：

- **振荡与不稳定**：遇到振荡和不稳定时，可以减小比例增益 \( K_p \)，或者增加微分增益 \( K_d \)来提高阻尼比。
- **稳态误差**：若存在稳态误差，则增