特征值分解实践手册：深入理解控制系统状态空间描述


# 摘要
本论文全面探讨了特征值分解在控制系统中的理论基础和实践技巧，并展望了其在控制系统设计和数据分析领域的进阶应用及未来发展方向。首先介绍了控制系统状态空间的基础知识，进而深入解析了特征值和特征向量的数学定义及其在系统稳定性分析中的作用。然后，详细阐述了特征值分解的几何意义、代数方法以及其在控制系统中的具体应用。文章还提供了特征值分解实践技巧，包括工具软件的应用、实例分析以及常见问题的解决方法。最后，探讨了特征值分解在系统能控性、能观性判定、极点配置、状态反馈控制以及状态估计等方面的应用，并讨论了复杂系统和机器学习领域的新挑战与应用前景。

# 关键字
特征值分解；控制系统；状态空间；能控性；能观性；机器学习

参考资源链接：[控制系统的状态空间基础：特征值与状态方程](https://wenku.csdn.net/doc/1yc9wyi57f?spm=1055.2635.3001.10343)
# 1. 控制系统状态空间基础

在现代控制系统设计中，状态空间模型提供了一种强大的工具，用于分析和设计动态系统。本章将介绍状态空间模型的基本概念，为理解后续章节的深入内容打下坚实基础。

## 状态空间模型概述

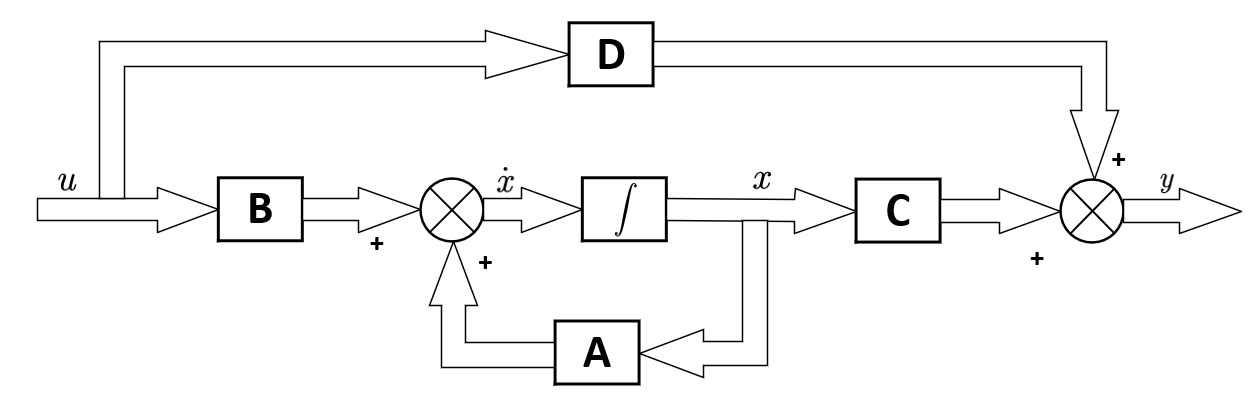
状态空间模型将控制系统描述为一组线性或非线性的一阶微分方程，它们表示系统状态的动态演化。在数学上，这样的模型通常由两个主要方程来表达：

\[
\begin{cases}
\dot{x}(t) = Ax(t) + Bu(t) \\
y(t) = Cx(t) + Du(t)
\end{cases}
\]

这里，\(x(t)\) 是状态向量，\(u(t)\) 是输入向量，\(y(t)\) 是输出向量，\(A\)、\(B\)、\(C\) 和 \(D\) 分别是系统矩阵、输入矩阵、输出矩阵和直接传递矩阵。状态向量的导数 \(\dot{x}(t)\) 描述了系统状态随时间的改变。

## 状态空间模型的重要性

状态空间模型之所以在控制系统中占据核心地位，是因为它为设计者提供了一种全面而灵活的方式来处理控制系统的设计问题。特别是，状态空间模型使得系统分析和综合过程在数学上更加严谨和系统化，允许工程师使用计算机辅助设计工具进行深入分析和模拟。

在下一章中，我们将深入探讨特征值和特征向量的理论，这是理解系统稳定性、控制器设计以及状态观测器构建的关键。通过掌握这些基础概念，我们将能够更好地利用状态空间模型，进一步深入控制系统设计的前沿领域。

# 2. 特征值分解理论详解

## 2.1 特征值和特征向量的数学定义

### 2.1.1 线性代数中特征值和特征向量的概念

在数学中，对于一个给定的n×n方阵A，如果存在标量λ和非零n维向量v使得关系式Av=λv成立，那么标量λ称为矩阵A的一个特征值，向量v被称为对应于λ的特征向量。这个定义深刻揭示了特征值和特征向量的本质，即特征值是矩阵的一个内在属性，它描述了矩阵对某个向量作用时的“缩放”效果，而特征向量则是指被缩放的向量。

从几何意义上讲，特征向量代表了空间中的一个方向，特征值则代表了这个方向上向量被矩阵变换时伸缩的比例。例如，在计算机图形学中，通过特征值和特征向量可以实现图形的旋转和缩放变换。在控制系统中，特征值则直接关联到系统状态的时间响应特性。

### 2.1.2 特征值在系统稳定性分析中的作用

在控制理论中，特征值分解能够用于分析系统的稳定性和动态响应。例如，考虑一个线性时不变系统，其动态可以用状态方程表示：

x'(t) = Ax(t)

其中，x(t)是状态向量，A是系统矩阵，而x'(t)是状态向量关于时间的导数。若系统矩阵A的所有特征值都具有负实部，则意味着系统的状态变量随时间衰减，系统是稳定的。反之，若存在一个或多个特征值具有正实部，则系统在相应方向上会表现出不稳定的行为，随时间演进，状态变量将会发散。

这种分析方法在设计控制器和分析系统行为时非常有用。例如，通过确保闭环系统的特征值均位于复平面的左半部分（即具有负实部），可以确保闭环系统是稳定的。这种分析方式为系统设计提供了重要的理论基础和实际操作指南。

## 2.2 特征值分解的几何意义和代数方法

### 2.2.1 几何意义下特征值与系统状态的关系

从几何的角度考虑，一个n维空间中的变换可以由其对应的矩阵表示。特征值和特征向量描述了这个变换作用于空间的基本方向和伸缩程度。具体来说，特征向量指向的每个方向在变换过程中保持不变，而其对应的特征值则表示了沿着这一方向伸缩的比例。

在系统稳定性分析中，这种几何关系意味着如果系统矩阵的特征值都位于左半复平面，那么系统状态在任意方向上的投影都会随时间衰减到零。相反，如果存在特征值位于右半复平面，那么系统状态在对应方向上将不断增长，导致系统不稳定。

例如，在研究简谐振子系统时，特征值决定了振子的自然频率和阻尼特性。具有正实部特征值的系统将表现为无阻尼或过阻尼振荡，而具有负实部特征值的系统则表现为欠阻尼振荡。

### 2.2.2 代数方法求解特征值和特征向量

在代数层面上，求解矩阵的特征值和特征向量涉及到求解特征多项式。对于给定的n阶方阵A，其特征多项式定义为：

det(A - λI) = 0

其中，I是单位矩阵，det表示行列式。这个方程是一个关于λ的多项式方程，其解（即根）就是矩阵A的特征值。在实际操作中，求解这个方程可能需要借助数值方法，尤其是当矩阵较大时。

一旦特征值被确定，我们就可以通过解线性方程组(A - λI)v=0来找到对应的特征向量，其中v是特征向量，λ是特征值。这个方程组的解空间给出了对应于特征值λ的所有特征向量。

以3×3矩阵为例，求解过程可能如下：

import numpy as np

A = np.array([[1, 2, 3],
              [0, 4, 5],
              [0, 0, 6]])

# 计算特征值
eigenvalues, _ = np.linalg.eig(A)
print("特征值:", eigenvalues)

# 计算特征向量
eigenvectors = np.linalg.eig(A)[1]
print("特征向量:\n", eigenvectors)

这个代码段首先使用NumPy库中的`eig`函数计算矩阵A的特征值和特征向量，然后打印结果。这便是代数方法在求解特征值和特征向量中的应用实例。

## 2.3 特征值分解在控制系统中的应用

### 2.3.1 控制系统中的特征值分解

在控制系统中，特征值分解帮助我们理解和设计系统的动态行为。特别是对于线性时不变系统，通过分析系统的状态矩阵A的特征值，我们可以预测系统的瞬态和稳态响应。例如，在电力系统的稳定性分析中，特征值分解被用来识别系统模式和潜在的振荡模式。

在实际应用中，工程师往往需要调整系统的参数以获得期望的动态行为。特征值分解为这种调整提供了理论指导。通过改变矩阵的元素，可以影响系统的特征值分布，从而改变系统的稳定性和响应速度。特征值分解技术在航空航天、机器人技术、自动驾驶车辆等领域都有广泛应用。

### 2.3.2 特征值分解在状态空间模型中的作用

状态空间模型是描述动态系统行为的数学模型，通常表示为一组线性微分方程。在状态空间模型中，特征值分解有助于分析系统稳定性和响应特性。通过状态空间模型，我们可以得到系统矩阵、输入矩阵和输出矩阵等关键参数，这些参数共同决定了系统的动态性能。

在设计控制系统时，工程师可以利用特征值分解来配置系统的极点，即系统的特征值。例如，将闭环系统的极点配置在左半复平面上，可以确保系统的稳定性和快速响应。此外，特征值分解还用于设计观测器和滤波器，从而实现对系统状态的估计和观测。

在计算机控制系统中，数值稳定性和计算精度是必须考虑的重要因素。因此，在应用特征值分解时，需要特别注意算法的稳定性和准确性。通过采用可靠的数值方法，如QR算法，可以有效地计算出矩阵的特征值和特征向量，为控制系统的分析和设计提供坚实的基础。

以上是第二章的核心内容，详细介绍了特征值和特征向量的基本概念、特征值分解的几何意义与代数计算方法，以及特征值分解在控制系统中的具体应用。这些知识构成了控制理论和系统分析的基石，并在工程实践中发挥着重要的作用