光学环形谐振器稳定性分析：理论与实验结果的对比研究


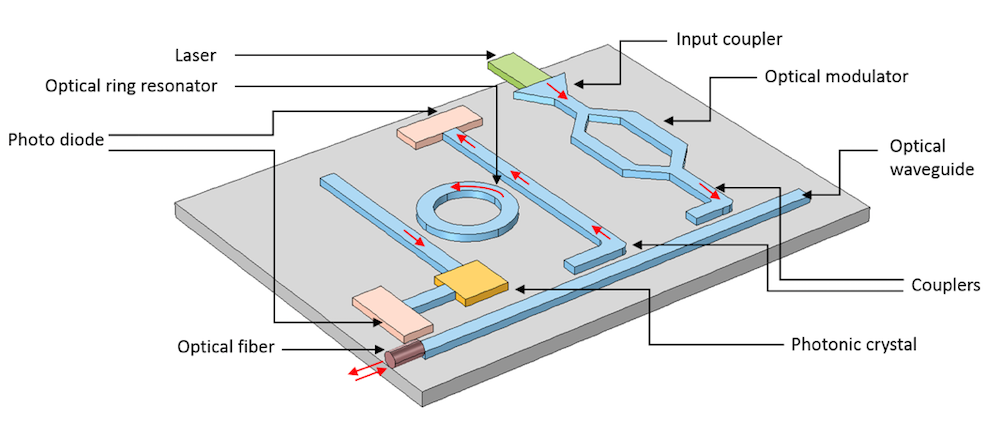
# 摘要
光学环形谐振器作为一种重要的光学元件，在传感、信号处理等领域具有广泛的应用。本文首先阐述了光学环形谐振器的基本原理，包括光波在谐振器中的传播模式、谐振条件及品质因子Q的定义。接着，通过稳定性理论模型对光学环形谐振器进行了静态和动态分析，并运用有限元分析(FEA)等数值模拟技术，与理论预测进行对比。实验设计与实现章节详细介绍了实验装置的搭建、参数的测量与控制，以及数据的收集与分析。在理论与实验结果对比研究中，本文对光学环形谐振器的稳定性进行了深入分析，并讨论了精度提升及误差来源。最后，在结论与展望章节总结了研究成果，并对光学环形谐振器的应用前景与未来研究方向进行了展望。

# 关键字
光学环形谐振器；传播模式；品质因子Q；稳定性分析；数值模拟；误差分析

参考资源链接：[COMSOL模拟：光学环形谐振腔陷波滤波器设计与分析](https://wenku.csdn.net/doc/5azpdv5ecd?spm=1055.2635.3001.10343)
# 1. 光学环形谐振器的基本原理

## 1.1 光学环形谐振器简介

光学环形谐振器(Optical Ring Resonator, ORR)是一种能够捕获并维持特定频率光波的器件，其应用广泛，从基础物理研究到现代光通信技术中扮演着重要角色。本章将介绍光学环形谐振器的基础知识，为理解后续章节的理论分析、数值模拟及实验设计打下基础。

## 1.2 基本结构与功能

光学环形谐振器的典型结构由一个或多个弯曲的波导构成，形成了封闭或半封闭的光路。光波在环形路径中传播时，特定频率的光波会在谐振器中形成谐振现象，即在特定条件下增强或减弱。这种选择性增强特定频率光波的特性，使得ORR在滤波器、传感器和激光器等领域具有重要应用。

## 1.3 工作原理简述

工作原理基于光的全内反射与谐振效应。当满足特定的频率条件时，环形路径中的光波会产生相长干涉，形成谐振峰。谐振条件通常与环形路径长度、折射率及波导的耦合效率有关。理解这些基本原理对于设计高性能光学环形谐振器至关重要。

graph LR
A[入射光] -->|全内反射| B[波导路径]
B -->|相长干涉| C[谐振峰值]
C --> D[输出光]

以上简单的流程图形象地展示了光在光学环形谐振器内的传播与谐振过程。下一章节将深入分析光学环形谐振器的工作原理和理论模型。

# 2. 理论分析与数值模拟

## 2.1 光学环形谐振器的工作原理

### 2.1.1 光波在谐振器中的传播模式

光学环形谐振器（Ring Resonator）是一种利用光波在环形路径上多次循环传播的装置，其基本工作原理涉及光波在谐振腔中的模式共振。在环形谐振器中，光波以特定的模式在环形路径上反复循环，只有当光波的循环次数与谐振条件相匹配时，才能形成稳定的共振。

在分析光波在环形谐振器中的传播模式时，通常考虑其传输方程：

E_{\text{out}}(t) = E_{\text{in}}(t-\tau)e^{-\alpha L}

其中，\(E_{\text{out}}(t)\) 表示输出光场，\(E_{\text{in}}(t-\tau)\) 表示输入光场延迟了时间 \(\tau\)，\(L\) 是环形路径的长度，而 \(\alpha\) 是介质损耗系数。为了形成共振，光波在环形路径上必须满足相位匹配条件：

\beta L = 2\pi m

其中，\(\beta\) 是传播常数，\(m\) 是整数，表示光波的循环次数。

### 2.1.2 谐振条件与品质因子Q的定义

谐振条件是光学环形谐振器设计和应用中的核心。环形谐振器的谐振频率 \(f\) 可以通过以下公式确定：

f = \frac{c}{n\lambda}

其中，\(c\) 是光速，\(n\) 是介质的折射率，\(\lambda\) 是光波的波长。只有在特定频率下，才能在环形路径上形成稳定的共振。

品质因子 \(Q\) 是描述谐振器性能的重要参数，定义为存储在谐振器内的能量与每圈循环能量损失之比：

Q = 2\pi \frac{\text{能量存储}}{\text{每圈能量损耗}}

高 \(Q\) 值意味着谐振器的损耗低，能量存储时间长，从而具有更高的稳定性和分辨率。

## 2.2 稳定性理论模型

### 2.2.1 静态稳定性分析

静态稳定性分析主要关注在没有外部扰动时，系统能否保持稳定。对于光学环形谐振器而言，静态稳定性分析需要考虑内部损耗、外部耦合以及光波长变化等因素。

静态稳定性分析可以通过特征方程的方法来完成。考虑一个简单的谐振器模型，特征方程通常具有如下形式：

A\cos(\omega \tau) + B\sin(\omega \tau) = 1

其中，\(A\) 和 \(B\) 是与谐振器的物理参数相关的常数，\(\omega\) 是角频率，\(\tau\) 是光波在环形路径上的往返时间。求解此方程可以得到静态稳定的工作点。

### 2.2.2 动态稳定性分析

动态稳定性分析则涉及到系统对外部扰动的响应，包括温度变化、机械振动和光强波动等因素的影响。

动态稳定性可以通过分析系统对于小扰动的反应来评估。考虑扰动后的动态方程为：

\frac{dE}{dt} = -j\omega_0 E + \kappa E_{\text{in}}(t)

其中，\(E\) 是振幅，\(\omega_0\) 是谐振频率，\(\kappa\) 是耦合系数，\(E_{\text{in