【MATLAB电路仿真实战指南】：从小白到专家的进阶攻略

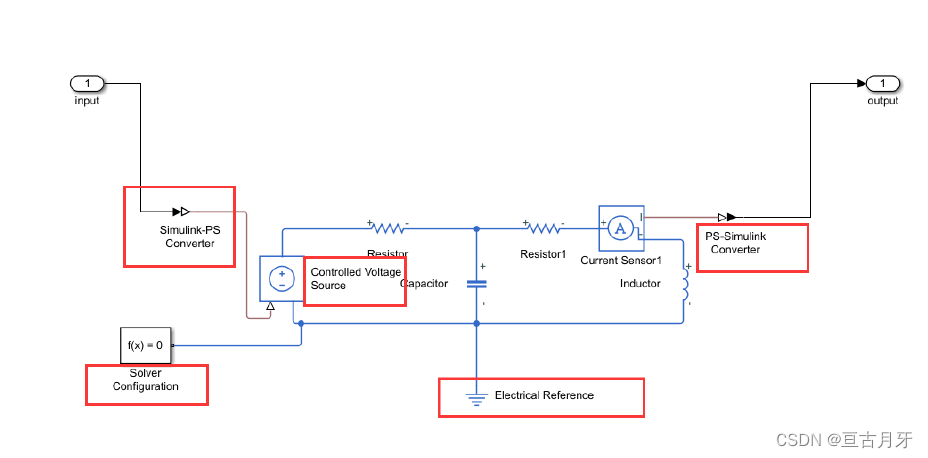
# 1. MATLAB电路仿真基础

MATLAB电路仿真是利用MATLAB软件对电路进行建模、分析和优化的过程。它提供了一个强大的平台，使工程师能够轻松高效地设计和验证电路。

### 1.1 MATLAB电路仿真优势

MATLAB电路仿真具有以下优势：

- **交互式环境：**MATLAB提供了一个交互式环境，允许工程师快速探索不同设计选项。
- **丰富的库：**MATLAB包含一个广泛的电路元件库，使建模变得更加容易。
- **高级分析工具：**MATLAB提供了一系列高级分析工具，如直流、交流和瞬态分析，用于深入了解电路行为。
- **可扩展性：**MATLAB可以与其他工具和语言集成，以扩展其功能。

# 2. 电路仿真建模技巧

### 2.1 电路元件建模

电路仿真建模是电路仿真过程中的关键步骤，它涉及到将电路元件转换为数学模型，以便计算机能够对电路进行分析。MATLAB 提供了丰富的库和工具，可以简化电路元件建模的过程。

#### 2.1.1 电阻建模

电阻是最基本的电路元件，其数学模型为：

V = IR

其中：

- V 为电阻两端的电压
- I 为流过电阻的电流
- R 为电阻的阻值

在 MATLAB 中，可以使用 `resistor` 函数来创建电阻对象：

R = resistor(10); % 创建一个阻值为 10 欧姆的电阻

#### 2.1.2 电容建模

电容是一种能够存储电荷的元件，其数学模型为：

I = C * dV/dt

其中：

- I 为流过电容的电流
- C 为电容的电容值
- V 为电容两端的电压

在 MATLAB 中，可以使用 `capacitor` 函数来创建电容对象：

C = capacitor(1e-6); % 创建一个电容值为 1 uF 的电容

#### 2.1.3 电感建模

电感是一种能够存储磁能的元件，其数学模型为：

V = L * di/dt

其中：

- V 为电感两端的电压
- L 为电感的电感值
- i 为流过电感的电流

在 MATLAB 中，可以使用 `inductor` 函数来创建电感对象：

L = inductor(1e-3); % 创建一个电感值为 1 mH 的电感

### 2.2 电路分析方法

MATLAB 提供了多种电路分析方法，包括：

#### 2.2.1 直流分析

直流分析用于分析电路在直流条件下的行为。MATLAB 中可以使用 `dcOperatingPoint` 函数进行直流分析：

result = dcOperatingPoint(circuit); % 对电路进行直流分析

#### 2.2.2 交流分析

交流分析用于分析电路在交流条件下的行为。MATLAB 中可以使用 `acAnalysis` 函数进行交流分析：

result = acAnalysis(circuit, frequency); % 对电路进行交流分析，指定频率为 frequency

#### 2.2.3 瞬态分析

瞬态分析用于分析电路在时间域内的行为。MATLAB 中可以使用 `transientAnalysis` 函数进行瞬态分析：

result = transientAnalysis(circuit, time_span); % 对电路进行瞬态分析，指定时间跨度为 time_span

### 2.3 模型验证和优化

#### 2.3.1 模型验证方法

模型验证是确保电路仿真模型准确性的重要步骤。MATLAB 中可以使用以下方法进行模型验证：

- **实验验证：**将仿真结果与实际电路的测量结果进行比较。
- **分析验证：**使用分析方法（如手算或其他仿真工具）来验证仿真结果。

#### 2.3.2 模型优化策略

模型优化可以提高电路仿真模型的准确性和效率。MATLAB 中可以使用以下策略进行模型优化：

- **参数优化：**调整模型中的参数，以最小化与实验或分析结果的误差。
- **拓扑优化：**修改模型的拓扑结构，以提高仿真效率或准确性。
- **算法优化：**选择合适的仿真算法，以提高仿真速度或收敛性。

# 3. MATLAB电路仿真实践

### 3.1 电路故障诊断

MATLAB在电路故障诊断中发挥着至关重要的作用，因为它可以快速准确地识别和定位电路中的故障。常见的电路故障包括开路、短路和接触不良。

#### 3.1.1 开路故障诊断

开路故障是指电路中的导线或元件断开，导致电流无法流动。MATLAB可以通过以下步骤诊断开路故障：

1. **测量电压和电流：**使用MATLAB的测量工具测量电路中各点的电压和电流。开路故障会引起电压或电流异常，例如电压降为零或电流为零。
2. **分析阻抗：**计算电路各点的阻抗。开路故障会使阻抗急剧增加。
3. **绘制波形：**绘制电压和电流的波形图。开路故障会引起波形异常，例如电压或电流突然下降或消失。

#### 3.1.2 短路故障诊断

短路故障是指电路中两个或多个导线或元件意外连接，导致电流过大。MATLAB可以通过以下步骤诊断短路故障：

1. **测量电压和电流：**测量电路中各点的电压和电流。短路故障会引起电压或电流异常，例如电压降为零或电流急剧增加。
2. **分析阻抗：**计算电路各点的阻抗。短路故障会使阻抗急剧减小。
3. **绘制波形：**绘制电压和电流的波形图。短路故障会引起波形异常，例如电压或电流突然上升或出现尖峰。

#### 3.1.3 接触不良故障诊断

接触不良故障是指电路中的连接点松动或氧化，导致电流流动不稳定。MATLAB可以通过以下步骤诊断接触不良故障：

1. **测量电压和电流：**测量电路中各点的电压和电流。接触不良故障会引起电压或电流波动或间歇性中断。
2. **分析阻抗：**计算电路各点的阻抗。接触不良故障会引起阻抗不稳定或波动。
3. **绘制波形：**绘制电压和电流的波形图。接触不良故障会引起波形异常，例如电压或电流出现尖峰或波动。

### 3.2 电路性能评估

MATLAB还可以用于评估电路的性能，包括电压和电流分析、功率和效率分析以及谐波分析。

#### 3.2.1 电压和电流分析

MATLAB可以测量和分析电路中的电压和电流。通过绘制波形图、计算峰值和均值，可以评估电路的稳定性、效率和响应时间。

#### 3.2.2 功率和效率分析

MATLAB可以计算电路的功率和效率。通过测量电压、电流和功率因数，可以评估电路的功耗、效率和功率质量。

#### 3.2.3 谐波分析

MATLAB可以执行谐波分析，以识别和量化电路中存在的谐波成分。谐波分析对于评估电路的电磁兼容性（EMC）和功率质量至关重要。

### 3.3 电路设计优化

MATLAB还可用于优化电路设计。通过参数优化、拓扑优化和算法优化，可以提高电路的性能和效率。

#### 3.3.1 参数优化

MATLAB可以优化电路中的参数，例如电阻、电容和电感的值。通过使用优化算法，可以找到参数的最佳组合，以满足特定的设计目标，例如最大化效率或最小化功耗。

#### 3.3.2 拓扑优化

MATLAB可以优化电路的拓扑结构。通过探索不同的拓扑结构，可以找到最适合特定应用的拓扑结构。

#### 3.3.3 算法优化

MATLAB可以优化电路仿真算法。通过调整算法参数，可以提高仿真速度和精度。

# 4. MATLAB电路仿真进阶

### 4.1 电路仿真高级分析

#### 4.1.1 参数扫描分析

参数扫描分析是一种通过改变电路中的特定参数值来研究其性能变化的技术。它可以用于识别关键参数、优化设计并探索设计空间。

**代码块：**

% 参数扫描范围
param_range = [0.1:0.01:1];

% 循环遍历参数值
for param_value = param_range
    % 设置参数值
    set_param(model, 'param_name', num2str(param_value));
    % 运行仿真
    sim(model);
    % 提取仿真结果
    results = get_param(model, 'results');
    % 存储结果
    data(param_value, :) = results;
end

**逻辑分析：**

* 该代码块使用`param_range`变量定义参数扫描范围。
* 循环遍历参数值，并使用`set_param`函数设置模型中的参数值。
* 运行仿真并提取仿真结果。
* 将结果存储在`data`变量中，以供进一步分析。

#### 4.1.2 蒙特卡罗分析

蒙特卡罗分析是一种基于概率的分析技术，用于评估电路在随机变量的影响下的性能。它可以用于评估设计鲁棒性、识别敏感参数并进行风险分析。

**代码块：**

% 定义随机变量
random_variables = {'param1', 'param2', 'param3'};

% 生成随机变量的样本
samples = lhsdesign(3, 100);

% 循环遍历样本
for i = 1:size(samples, 1)
    % 设置随机变量值
    for j = 1:length(random_variables)
        set_param(model, random_variables{j}, num2str(samples(i, j)));
    end
    % 运行仿真
    sim(model);
    % 提取仿真结果
    results = get_param(model, 'results');
    % 存储结果
    data(i, :) = results;
end

**逻辑分析：**

* 该代码块使用`lhsdesign`函数生成随机变量的样本。
* 循环遍历样本，并使用`set_param`函数设置模型中的随机变量值。
* 运行仿真并提取仿真结果。
* 将结果存储在`data`变量中，以供进一步分析。

#### 4.1.3 优化算法应用

优化算法可以用于优化电路设计，以满足特定目标。MATLAB提供了各种优化算法，包括遗传算法、粒子群优化和模拟退火。

**代码块：**

% 定义优化目标
objective = @(params) get_objective(params);

% 定义优化算法
optimizer = ga;

% 设置优化参数
optimizer.PopulationSize = 50;
optimizer.Generations = 100;

% 运行优化
[optimal_params, optimal_value] = run(optimizer, objective);

**逻辑分析：**

* 该代码块使用`get_objective`函数定义优化目标。
* 选择遗传算法作为优化算法，并设置优化参数。
* 运行优化，并获得最优参数和最优值。

# 5. MATLAB电路仿真进阶

**5.1 电路仿真高级分析**

MATLAB提供了多种高级分析工具，用于深入了解电路行为。

**5.1.1 参数扫描分析**

参数扫描分析允许在指定范围内对电路参数进行系统地变化，并观察其对电路响应的影响。这对于识别关键参数和优化电路性能非常有用。

% 定义参数范围
param_range = linspace(0.1, 1, 10);

% 循环遍历参数值
for param_value = param_range
    % 更新电路参数
    circuit.param = param_value;
    % 运行仿真
    result = simulate(circuit);
    % 存储结果
    results(param_value) = result;
end

% 绘制响应曲线
plot(param_range, results);

**5.1.2 蒙特卡罗分析**

蒙特卡罗分析是一种统计方法，用于评估电路在参数不确定性下的性能。它通过生成大量随机参数组合并运行仿真来实现。

% 定义参数分布
param_distributions = {
    'normal', 0.5, 0.1;
    'uniform', 0.4, 0.6;
    'lognormal', 1, 0.2
};

% 生成随机参数组合
params = generate_random_parameters(param_distributions, 1000);

% 循环遍历参数组合
for i = 1:size(params, 1)
    % 更新电路参数
    circuit.params = params(i, :);
    % 运行仿真
    result = simulate(circuit);
    % 存储结果
    results(i) = result;
end

% 分析结果
[mean_result, std_result] = analyze_results(results);

**5.1.3 优化算法应用**

MATLAB提供了各种优化算法，用于自动优化电路性能。这些算法可以找到一组参数值，以最小化或最大化目标函数。

% 定义目标函数
objective_function = @(params) evaluate_circuit(params);

% 定义优化算法
optimizer = optimset('Algorithm', 'fmincon');

% 运行优化
optimal_params = fmincon(objective_function, initial_params, [], [], [], [], lower_bounds, upper_bounds, [], optimizer);

% 评估优化后的电路
optimized_result = simulate(circuit, optimal_params);