【双输入单输出模糊控制器实战手册】:性能评估与优化策略
发布时间: 2024-12-23 09:50:29 阅读量: 11 订阅数: 11 


12123.zip_S8A_weekmxf_两输入三输出模糊控制器规则
# 摘要
模糊控制技术作为智能控制领域的一种关键技术,近年来在自动化和决策支持系统中得到了广泛应用。本文系统地介绍了双输入单输出模糊控制器的基础理论、设计实现、性能评估方法和优化策略。通过阐述模糊逻辑、模糊集合理论以及模糊规则的构建,本文详细说明了双输入单输出模糊控制器的设计与实现过程。性能评估章节着重于评估指标的选取和评估实验的设计,旨在确保控制器的精确度、稳定性和响应时间。最后,本文探讨了模糊控制器的优化策略和实际应用案例,以及未来模糊控制技术的发展趋势与面临的挑战。通过深入分析,本文旨在为研究者和工程技术人员提供完整的模糊控制器开发与应用框架。
# 关键字
双输入单输出;模糊控制器;模糊逻辑;性能评估;参数优化;结构优化;实际应用
参考资源链接:[模糊控制规则详解:双输入-单输出与多输入设计](https://wenku.csdn.net/doc/ua6a7wq6nm?spm=1055.2635.3001.10343)
# 1. 双输入单输出模糊控制器基础
在当今的自动化与智能控制系统中,双输入单输出模糊控制器因其在处理不确定性信息和非线性系统中的出色表现而成为研究和应用的热点。该章节将引领读者入门,了解模糊控制的基础知识,为深入探讨设计、实现和性能评估等后续内容打下坚实的基础。
## 1.1 模糊控制的定义与原理
模糊控制是一种基于模糊逻辑的控制方法,旨在模仿人类的决策过程来处理不确定和模糊的问题。它利用模糊集合、隶属函数和模糊规则,将精确的输入值转换为模糊语言变量,通过模糊推理实现对输出的控制。
## 1.2 模糊控制器的基本组成部分
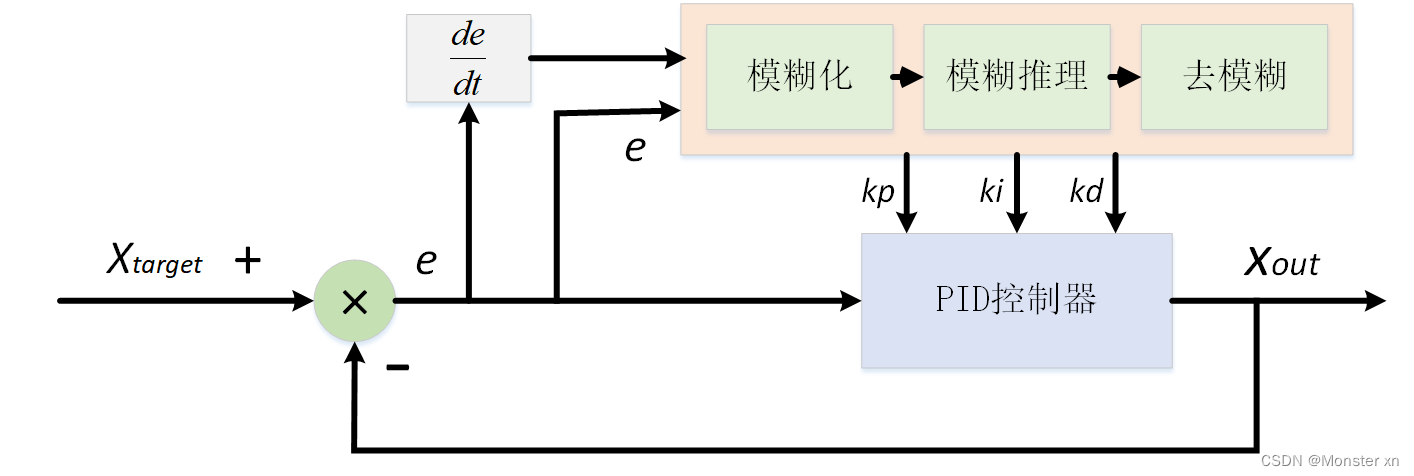
一个典型的双输入单输出模糊控制器由输入模糊化、规则库、模糊推理机和输出去模糊化四个基本组成部分构成。每部分均在模糊控制过程中扮演关键角色,其设计的优劣直接影响控制器的整体性能。
## 1.3 控制器在实际问题中的应用
模糊控制器广泛应用于各种实际问题的解决方案中,尤其在温度控制、交通信号灯管理等难以用精确数学模型描述的场合,双输入单输出模糊控制器提供了一种既简便又有效的控制策略。接下来的章节将详细介绍如何设计、实现、评估和优化这种控制器。
# 2. 模糊控制器的设计与实现
模糊控制器的设计与实现是模糊控制理论中的一个核心环节,涉及多个关键步骤,从理论基础到具体编码实现,每个环节都至关重要。在本章中,我们将深入探讨如何设计与实现一个双输入单输出模糊控制器。
### 2.1 模糊控制器的理论基础
在开始设计模糊控制器之前,我们需要掌握它的理论基础,特别是模糊逻辑与模糊集合理论,以及模糊规则的构建与推理机制。
#### 2.1.1 模糊逻辑与模糊集合理论
模糊逻辑是一种处理不确定性信息的工具,与传统的布尔逻辑不同,模糊逻辑允许部分真值的存在。例如,在传统逻辑中,一个陈述可以是真或假,而在模糊逻辑中,一个陈述可以是半真半假。模糊集合的概念由L.A. Zadeh于1965年提出,是模糊逻辑的基础。模糊集合理论通过模糊集合来表示模糊概念,其中的元素隶属度不是0或1,而是介于两者之间的任何值。隶属度函数是模糊集合的核心,它定义了元素对模糊集合的隶属程度。
#### 2.1.2 模糊规则的构建与推理机制
模糊规则是模糊控制器的核心,它们基于人类的直观知识和经验,通过“如果-那么”规则来表达。例如:“如果温度很高,那么风扇应该转得很快。”模糊规则通常描述输入变量和输出变量之间的关系,并依赖于模糊集合理论。在模糊推理中,这些规则是通过模糊逻辑运算符(例如“与”,“或”,“非”)来组合和推理的。一个模糊控制器可能包含数十到数百条这样的规则。
### 2.2 设计双输入单输出模糊控制器
设计一个双输入单输出(SISO)模糊控制器需要仔细考虑输入输出变量的模糊化和规则库的设计与决策过程。
#### 2.2.1 输入输出变量的模糊化
模糊化是指将精确的输入数据转化为模糊集合中的隶属度值的过程。例如,如果一个输入变量是温度,那么它可能被模糊化为“冷”,“适中”,和“热”三个模糊集。在模糊控制器中,通常会定义一系列的模糊集合,比如用“低”、“中”、“高”来描述温度的不同程度。
#### 2.2.2 规则库的设计与决策过程
规则库是模糊控制器的灵魂,它包含了所有的模糊规则。设计规则库时,工程师需要综合考虑系统的动态特性以及可能的输入状态。在模糊控制器的决策过程中,首先使用模糊规则库中的规则对模糊化的输入进行模糊推理,然后通过模糊决策方法(例如,加权平均法、最大隶属度法等)得到模糊化的输出。最后,通过逆模糊化过程,将模糊化的输出转换为精确的控制动作。
### 2.3 模糊控制器的编码与测试
编码实践涉及将模糊控制器的设计转化为实际可以运行的代码。测试与验证则是确保控制器性能的关键步骤。
#### 2.3.1 编码实践:从设计到实现
在编码实践中,首先需要选择合适的编程环境和语言,如MATLAB、Python或C++。然后,根据模糊控制器的设计,逐步实现模糊集的定义、隶属度函数、模糊规则的编码以及模糊推理引擎。在编码时,我们通常需要构建数据结构来存储模糊集合和规则,并编写算法来执行模糊化、推理和逆模糊化。
**示例代码片段:**
```python
import numpy as np
import skfuzzy as fuzz
# 定义输入变量的模糊集合
temperature = fuzz.defuzz([0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100], np.arange(0, 101, 10), 'trimf')
humidity = fuzz.defuzz([0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100], np.arange(0, 101, 10), 'trimf')
# 定义隶属度函数
temperature_low = fuzz.trimf(temperature.universe, [0, 0, 50])
temperature_high = fuzz.trimf(temperature.universe, [50, 100, 100])
humidity_low = fuzz.trimf(humidity.universe, [0, 0, 50])
humidity_high = fuzz.trimf(humidity.universe, [50, 100, 100])
# 定义模糊规则
rule1 = "if temperature is high and humidity is low then output is 100"
rule2 = "if temperature is low and humidity is high then output is 0"
# 模糊推理
# 这里省略了模糊推理的实现过程,通常需要使用模糊逻辑库进行。
# 逆模糊化,获得精确输出
fuzzy_output = fuzz.defuzz([0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100], np.arange(0, 101, 10), 'trimf')
```
在上述代码中,我们首先定义了输入变量(温度和湿度)的模糊集合,然后使用模糊逻辑库(在这个例子中是`skfuzzy`)来实现模糊化、模糊规则定义以及逆模糊化的过程。这仅仅是一个简单的示例,实际的模糊控制器实现会更加复杂,需要考虑更多的模糊集合和规则。
#### 2.3.2 测试与验证:确保控制器性能
0
0






