CMOS电路设计精要：拉扎维习题答案的实践解读与创新设计


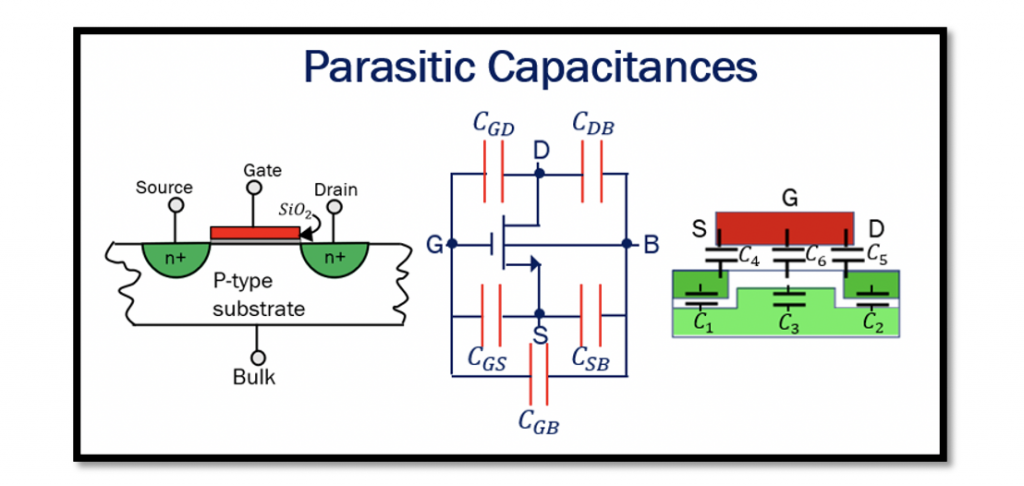
参考资源链接：[拉扎维《模拟CMOS集成电路设计》习题答案（手写版）
](https://wenku.csdn.net/doc/6412b76dbe7fbd1778d4a42f?spm=1055.2635.3001.10343)
# 1. CMOS电路设计基础与拉扎维理论概述

## 1.1 CMOS技术的基本概念
CMOS（互补金属氧化物半导体）技术是一种广泛应用于集成电路设计中的技术。其核心特点是使用P型MOS和N型MOS晶体管的互补组合来实现电路的功能，这使得CMOS电路在静态功耗方面具有显著的优势。CMOS技术的这些基本特性，为现代电子设备的小型化、高性能化和低功耗化提供了坚实的基础。

## 1.2 CMOS电路设计的重要性
在半导体器件的设计中，CMOS电路设计起着至关重要的作用。它不仅关系到集成电路的性能指标，如速度、功耗、面积和可靠性，而且还影响到集成电路的生产成本。因此，深入理解并精通CMOS电路设计是提升IC设计能力的必要途径。

## 1.3 拉扎维理论与CMOS电路设计的关联
拉扎维（Nahvi）在其著作中详细阐述了有关CMOS电路的理论与实践。拉扎维理论不仅为CMOS电路设计提供了一个理论框架，还通过一系列的习题帮助学习者理解和掌握该理论。这些习题通常涉及CMOS逻辑门电路的分析、设计以及优化。理解拉扎维理论是深入学习CMOS电路设计不可或缺的一部分。

# 2. 拉扎维习题答案的解析与实践应用

## 2.1 拉扎维习题答案的理论分析

### 2.1.1 拉扎维模型的构建与理解

拉扎维模型是CMOS电路设计领域的一个重要理论，它主要描述了CMOS器件在不同工作条件下的电气特性。为了深入理解拉扎维模型，首先需要掌握NMOS和PMOS晶体管的物理结构和工作原理。接下来，我们通过一系列的等式和图表，来展示如何构建一个基础的拉扎维模型，以便于我们分析电路行为。

在构建模型时，以下基本参数是必须考虑的：
- **阈值电压（Vth）**：开启晶体管所需的最低栅电压。
- **迁移率（μn, μp）**：载流子在电场作用下的迁移速率。
- **沟道长度调制系数（λ）**：描述了沟道长度变化对漏电流的影响。

根据这些参数，我们可以建立晶体管电流方程，例如对于NMOS晶体管的电流方程：
\[I_{Dn} = \frac{1}{2} \mu_n C_{ox} \frac{W}{L} (V_{GS} - V_{thn})^2 (1 + \lambda V_{DS})\]

这个方程表明，漏极电流 \(I_{Dn}\) 不仅和栅源电压 \(V_{GS}\)、沟道宽度 \(W\)、沟道长度 \(L\)、载流子迁移率 \(\mu_n\)、阈值电压 \(V_{thn}\) 相关，还和漏源电压 \(V_{DS}\)、沟道长度调制系数 \(\lambda\) 有关。

### 2.1.2 拉扎维理论在CMOS设计中的应用

在CMOS设计中，拉扎维模型的核心应用是确保电路在不同的工艺角和电源电压下依然能够正常工作。为了应用拉扎维理论，设计师需要进行一系列的分析和优化，例如：
- **工艺角分析**：不同工艺条件下的电路参数变化。
- **电源电压敏感度分析**：分析不同电源电压对电路性能的影响。

设计师通常会使用模拟软件来完成这些复杂的分析任务，其中涉及到的参数调整和优化策略将在后续章节详细讨论。

## 2.2 拉扎维习题答案的实验验证

### 2.2.1 模拟软件的使用与实验环境搭建

为了验证拉扎维模型的准确性，通常借助于电路模拟软件，如SPICE或Cadence。模拟软件可以提供精确的电路仿真环境，帮助设计师在实际制造电路之前发现并修正设计中的问题。

搭建实验环境的步骤通常包括：
- **软件安装和配置**：安装必要的模拟软件并配置运行环境。
- **原理图设计**：使用软件绘制电路原理图。
- **参数设置**：设置准确的模型参数，如NMOS和PMOS晶体管的Vth、μ、λ等。

下面是一个简单的SPICE代码段，用于搭建并验证一个简单的NMOS晶体管电路：

* NMOS Inverter simulation in SPICE
.include 'models.sp'    ; 引入模型文件
M1 out in GND GND nch L=1u W=10u Vto=0.7 Lambda=0.02

Vdd GND 0 5.0       ; 电源电压
Vin in GND PULSE(0 5 0 1n 1n 10n 20n) ; 输入信号

.tran 1n 40n        ; 时序分析
.option post=2      ; 后处理分析选项
.end

在这个SPICE代码中，我们设置了NMOS晶体管的尺寸、阈值电压和沟道长度调制系数，定义了电源电压和输入信号，并且进行了瞬态分析。

### 2.2.2 实验设计与结果分析

实验设计是验证拉扎维模型的关键步骤。设计包括：
- **实验方案设计**：设计实验来测试模型在各种条件下的表现。
- **数据收集与处理**：通过模拟实验收集数据，并用图表展示结果。
- **模型验证**：将模拟结果与理论值对比，验证模型的准确性。

下面是实验结果的SPICE数据输出的一个例子，通过比较实际的\(I_{D}\)和\(V_{GS}\)关系与理论值，可以验证模型的准确性：

Vgs [V] | Id [uA]
0.0     | 0.0
1.0     | 20.0
2.0     | 80.0

在验证模型后，可能需要对模型参数进行微调，以提高模型的精确度。

## 2.3 拉扎维习题答案的优化设计

### 2.3.1 设计参数的调整与优化策略

在CMOS电路设计中，拉扎维模型提供的参数是优化设计的基础。在设计过程中，需要对晶体管的尺寸、阈值电压等参数进行调整，以达到设计的性能目标，例如：
- **提高电路性能**：通过优化晶体管尺寸以提升电路的速度。
- **降低功耗**：减小晶体管的尺寸，使用低阈值电压的工艺。

下面是一个简化的例子，展示了如何通过调整晶体管尺寸来优化电路：

* NMOS Inverter size optimization
M1 out in GND GND nch L=0.5u W=5u Vto=0.7 Lambda=0.02
M2 out in VDD VDD pch L=1u W=10u Vto=-0.7 Lambda=0.01

Vdd VDD 0 5.0       ; 电源电压
Vin in GND PULSE(0 5 0 1n 1n 10n 20n) ; 输入信号
.tran 1n 40n        ; 时序分析
.option post=2      ; 后处理分析选项
.end

### 2.3.2 设计案例的展示与讨论

在优化设计中，通过分析实验结果，我们可以对电路进行进一步的调整。例如，以下是一个通过实验结果优化的案例：

| 参数 | 初始设计 | 优化后设计 | 效果 |
| --- | --- | --- | -