【坐标系选择的决定性影响】：专题讨论对模拟结果的影响


# 摘要
本文深入探讨了坐标系选择的理论基础及其在不同科学领域中的应用。通过分析直角坐标系、极坐标系、柱坐标系和球坐标系的特点与数学表达，本文揭示了不同类型坐标系在工程、物理、数学建模等场景下的适用性。同时，本文也探讨了坐标系转换的理论与方法，并分析了坐标系选择如何影响模拟结果的精确性和计算稳定性。此外，文章还提出了坐标系优化的方法，并对未来在计算机图形学、多物理场耦合等新兴领域的发展趋势进行了展望。本文最后提供了跨学科研究中坐标系创新的案例，并给出结论与实践建议，旨在指导实际应用中如何有效选择和优化坐标系，进而推动模拟领域的发展。

# 关键字
坐标系选择；数学表达；坐标转换；模拟结果；优化方法；跨学科研究

参考资源链接：[ADAMS教程：坐标系的位置与方向设定](https://wenku.csdn.net/doc/i1wn1io93i?spm=1055.2635.3001.10343)
# 1. 坐标系选择的理论基础

在科学研究与工程应用中，坐标系不仅是描述位置与方向的基础工具，而且对于简化问题求解、指导实验设计与技术开发具有重要意义。本章节将从坐标系的定义与基础概念出发，为读者呈现坐标系选择的理论基础，确保我们能够从正确的视角理解后续章节中将探讨的坐标系类型及其特点。

## 1.1 坐标系的定义与作用

**定义：**坐标系是由一组数轴（坐标轴）和原点组成的一套规则，用于在数学空间内唯一确定任何一点的位置。

**作用：**坐标系将抽象的数学概念具体化，为物理量、几何图形以及复杂系统的分析提供了具体的数学描述。它通过数值化的方法，使得复杂问题得以通过代数运算进行解析和数值计算。

## 1.2 坐标系的分类

按照不同的划分标准，坐标系可以有多种分类方式。通常，我们可以根据坐标轴的数量将其分为二维坐标系和三维坐标系；根据坐标轴之间的关系，又可以分为直角坐标系和非直角坐标系。在更具体的领域中，还会有柱坐标系、球坐标系等专用坐标系。

在下一章节，我们将详细探讨这些坐标系的类型及其特点，为读者提供一个全面的视角。在进入具体的类型分析之前，理解坐标系的基本定义与分类至关重要，因为这是选择合适坐标系的出发点。

# 2. 坐标系类型及其特点

### 2.1 常用坐标系概述

在处理各类工程与科学问题时，选择合适的坐标系是至关重要的一步。不同的坐标系有助于简化复杂问题，使得分析与计算变得更为便捷。以下分别介绍几种常用坐标系：

#### 2.1.1 直角坐标系

直角坐标系是最常见且易于理解的坐标系统，也被称为笛卡尔坐标系。在这个系统中，每个点的位置由三个互相垂直的坐标轴定义，分别是x轴、y轴和z轴。对于任意一点P，它的位置可以表示为三个数值(x, y, z)，这些数值对应于点P在各坐标轴上的投影距离。

直角坐标系广泛应用于工程设计、建筑图纸以及大部分日常生活中。其优点在于直观易用，适合于处理与直线或平面有关的问题。然而，在表示某些曲线或曲面问题时，使用直角坐标系可能会导致复杂的方程，这时采用其他类型的坐标系可能更为合适。

#### 2.1.2 极坐标系

极坐标系是一种平面坐标系，它通过一个角度和一个距离来定义点的位置。在极坐标系中，我们通常使用半径r（表示点与原点的距离）和角度θ（表示点与x轴正方向的夹角）来定位点。与直角坐标系不同，极坐标系下一个点的位置表示为(r, θ)，这使得它特别适合于处理旋转对称问题。

极坐标系在物理学中用于描述波动、电磁场等领域，同样在导航和天文学中也有着广泛的应用。其优点在于能够直观地描述旋转和周期性问题，但计算过程中需注意角度的转换以及极坐标与直角坐标之间的转换。

#### 2.1.3 柱坐标系和球坐标系

柱坐标系和球坐标系是对直角坐标系的进一步推广，分别用于解决三维空间中的特定问题。

柱坐标系采用三个参数：ρ（径向距离），φ（方位角），z（高度），而球坐标系则使用半径r，方位角θ以及倾角φ来描述点的位置。柱坐标系适合处理具有轴对称特征的问题，比如液体在圆柱形容器中的流动。而球坐标系在处理以某一点为中心向外辐射的问题时显示出其优越性，比如天体物理学中的问题。

这三种坐标系各有优劣，直角坐标系适用于描述一般三维空间问题，极坐标系和柱/球坐标系更适用于具有特定对称性的复杂几何结构问题。正确的坐标系选择可以大大简化数学表达式和计算过程。

### 2.2 各坐标系的数学表达和适用场景

#### 2.2.1 直角坐标系在工程中的应用

直角坐标系是工程绘图和设计中不可或缺的工具。例如，在建筑物的设计图纸中，工程师会使用直角坐标系来精确地表示各种结构的尺寸和位置。在计算机辅助设计（CAD）软件中，直角坐标系允许工程师以精确的坐标值来定义模型的每一个部分，使得设计更加高效和准确。

从数学的角度来看，直角坐标系下的函数表示通常比较简单。例如，三维空间中的一个平面可以表示为一个线性方程Ax + By + Cz + D = 0，而空间中的直线则可以用两个平面方程的交集来表示。这些方程的求解和操作都比较直观，因而直角坐标系在工程领域被广泛应用。

#### 2.2.2 极坐标系在物理中的应用

在物理学中，极坐标系特别适用于描述某些特定类型的物理现象。例如，在描述行星运动时，使用极坐标系能够更直观地表达行星相对于太阳的位置和运动。在这里，半径r代表行星与太阳之间的距离，角度θ则与行星的方位角相关。

在电磁学领域，极坐标系同样非常重要。对于分析在柱形导体周围的磁场，使用极坐标系可以将问题简化为二维问题来处理，从而避免了三维空间中的复杂计算。此外，极坐标系在量子力学和光学等领域的应用也相当广泛。

#### 2.2.3 柱坐标系与球坐标系在数学建模中的应用

在数学建模中，尤其是涉及到具有对称性的物理或工程问题时，柱坐标系和球坐标系显得格外有用。柱坐标系通常用于处理圆柱或圆柱形容器内部的流体动力学问题。例如，在石油工程中，井眼的流动状态就经常在柱坐标系中进行分析。使用柱坐标系可以将三维的流动问题简化为二维问题，简化了方程组的求解。

球坐标系在处理涉及球对称的问题时非常有用，比如在天体物理的模拟中描述恒星的引力场。球坐标系特别适合于描述那些在空间上以某点为中心呈辐射状分布的问题，例如地球磁场模型的构建和模拟。

### 2.3 坐标系转换的理论与方法

#### 2.3.1 点与向量的坐标转换

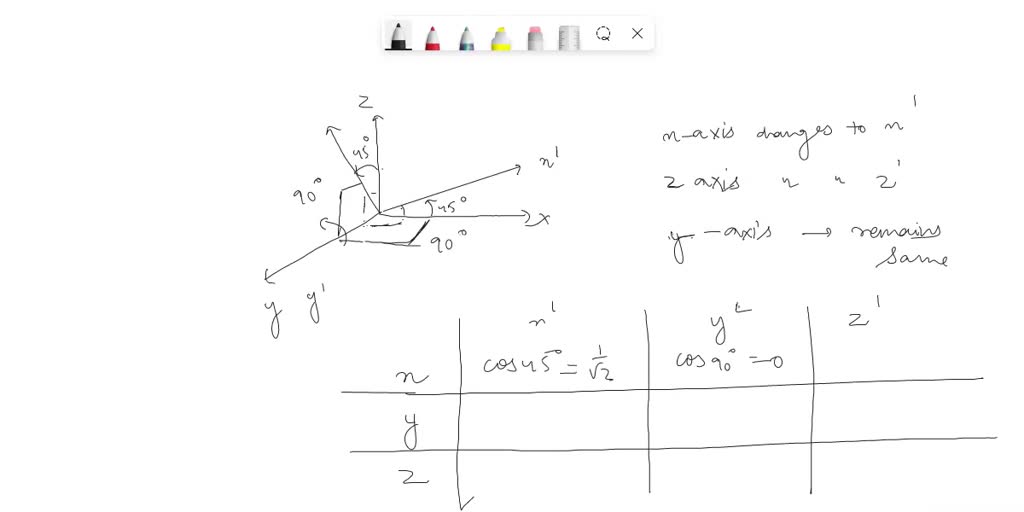
在不同的坐标系之间进行点与向量的坐标转换是数学与工程计算中的常见问题。这些转换可以基于定义良好的转换矩阵，该矩阵描述了源坐标系和目标坐标系之间的几何关系。例如，在三维空间中，从直角坐标系转换到球坐标系，可以使用如下转换公式：

r = sqrt(x^2 + y^2 + z^2)
θ = atan2(y, x)
φ = acos(